Area Calculator
Calculate area by selecting a shape and entering your measurements in any metric or US customary unit. See the formulas to find the area for each shape below.
Area Result:
On this page:
- Area Calculator
- How to Calculate Area
- Area Formulas
- How to Find Area of a Square
- How to Find Area of a Rectangle
- How to Find Area of a Trapezoid
- How to Find Area of a Parallelogram
- How to Find Area of a Rhombus
- How to Find Area of a Triangle
- How to Find Area of a Circle
- How to Find Area of an Ellipse
- How to Find Area of a Sector
- How to Find Area of a Segment
- How to Find Area of a Ring
- How to Find Area of a Pentagon
- How to Find Area of a Hexagon
- How to Find Area of an Octagon
- How to Find Area of a Regular Polygon
- How to Find Area of an Irregular Quadrilateral
- How to Find Area of a Compound Shape
- Frequently Asked Questions
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
Pateakia has worked in education for 15 years and has three degrees, including a PhD, Master's degree, and Bachelor's degree. She specializes in mathematics.
How to Calculate Area
In geometry, area is the space inside the perimeter or boundary of a space, and its symbol is (A). Area is the measurement of the size of a two-dimensional surface, unlike length, which is a unidimensional measurement.
Because it’s two-dimensional, area is measured in square units, for example, square feet or square meters. This indicates that it’s a measurement of one dimension by another dimension.
Area Formulas
Every geometric shape has a unique formula to calculate its area. Use the formulas below to find the area of many popular shapes.
| Shape | Formula |
|---|---|
| Square | A = a2 |
| Rectangle | A = l × w |
| Triangle | A = bh ÷ 2 |
| Trapezoid | A = 1/2(a + b)h |
| Parallelogram | A = b × h |
| Rhombus | A = a × h |
| Kite | A = pq ÷ 2 |
| Circle | A = πr2 |
| Semicircle | A = 1/2πr2 |
| Circular Ring | A = πR2 – πr2 |
| Ellipse | A = πab |
| Sector | A = (θ ÷ 360)πr2 |
| Pentagon | A = (a2 × 5) ÷ (4 × tan(π ÷ 5)) |
| Hexagon | A = (a2 × 6) ÷ (4 × tan(π ÷ 6)) |
| Octagon | A = (a2 × 8) ÷ (4 × tan(π ÷ 8)) |
| Polygon | A = (a2 × n) ÷ (4 × tan(π ÷ n)) |
| Irregular Quadrilateral | A = 1/2 × d × (h1 + h2) |
How to Find Area of a Square
A square is a polygon (two-dimensional shape) with four equal straight sides and four equal interior right angles.
The area of a square is equal to the edge length times the edge length, or the edge length squared.
A = a × a
a = edge length
How to Find Area of a Rectangle
A rectangle is a polygon with four straight sides and four interior right angles. Unlike a square, a rectangle’s adjacent sides have different lengths, but the opposing sides are equal.
The area of a rectangle is equal to the length times the width.
A = l × w
l = length
w = width
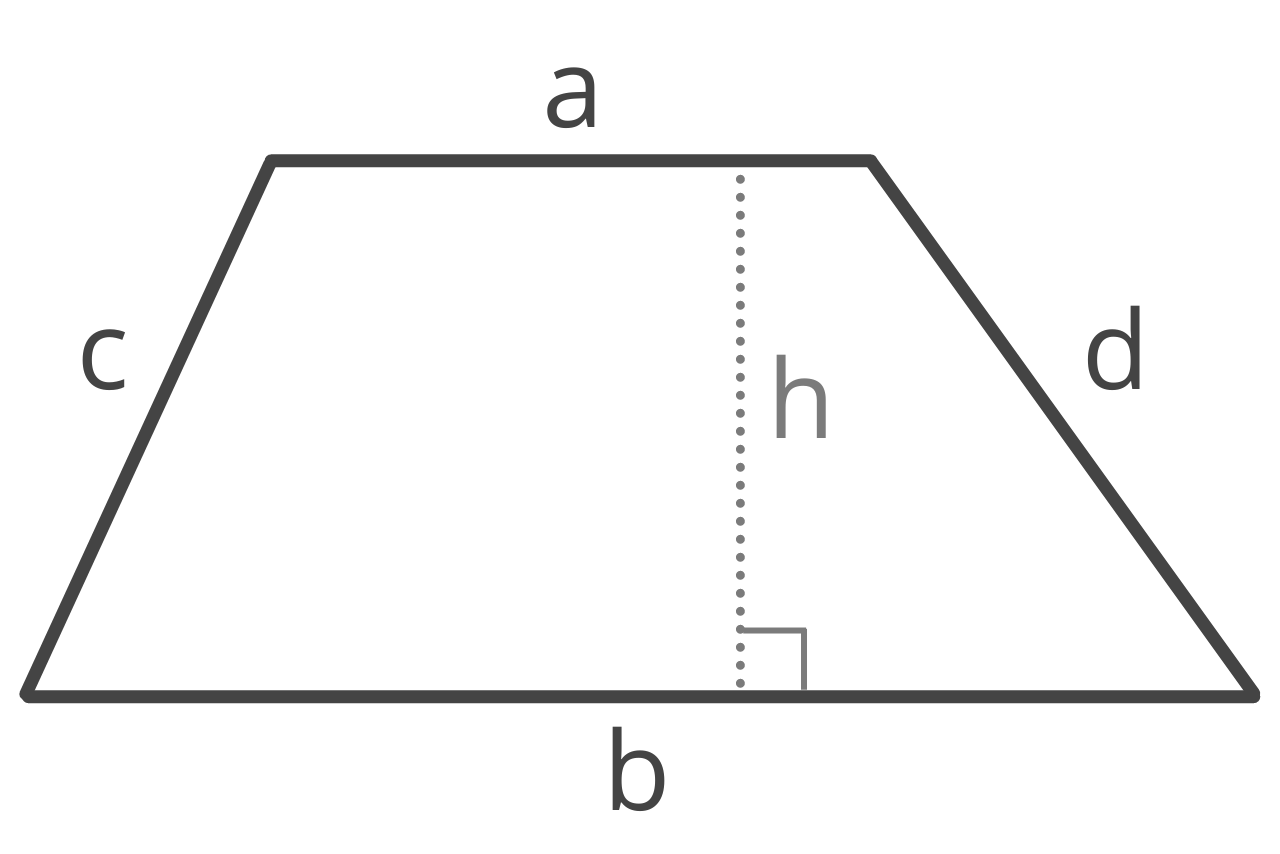
How to Find Area of a Trapezoid
A trapezoid is a polygon with four straight sides, and one pair of sides are parallel.
The parallel sides of the trapezoid are called its bases, while the non-parallel sides are called its legs. The perpendicular distance between the bases is called the height or altitude.
There are three types of trapezoids: right, isosceles, and scalene. The formula to calculate the area for all three types is one-half of the sum of the base lengths times the distance (height) between them.
A = 1/2(a + b)h
a = base a
b = base b
h = height
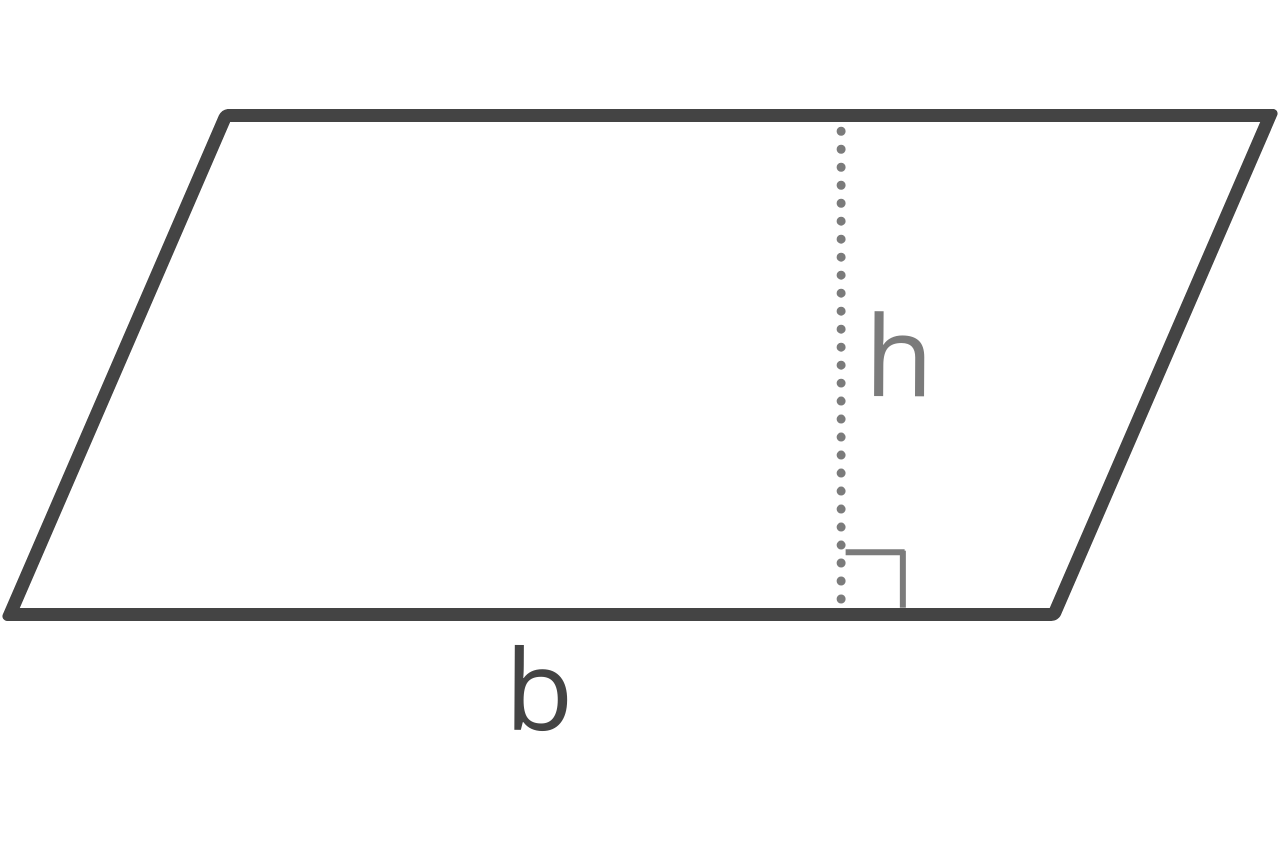
How to Find Area of a Parallelogram
A parallelogram is similar to a rectangle in that it is a polygon with four straight sides and the adjacent sides are different lengths. However, the opposing sides are equal. Unlike a rectangle, the interior angles are not right angles, and the opposing angles are equal to each other.
The area of a parallelogram is equal to the base length times the height.
A = b × h
b = base
h = height
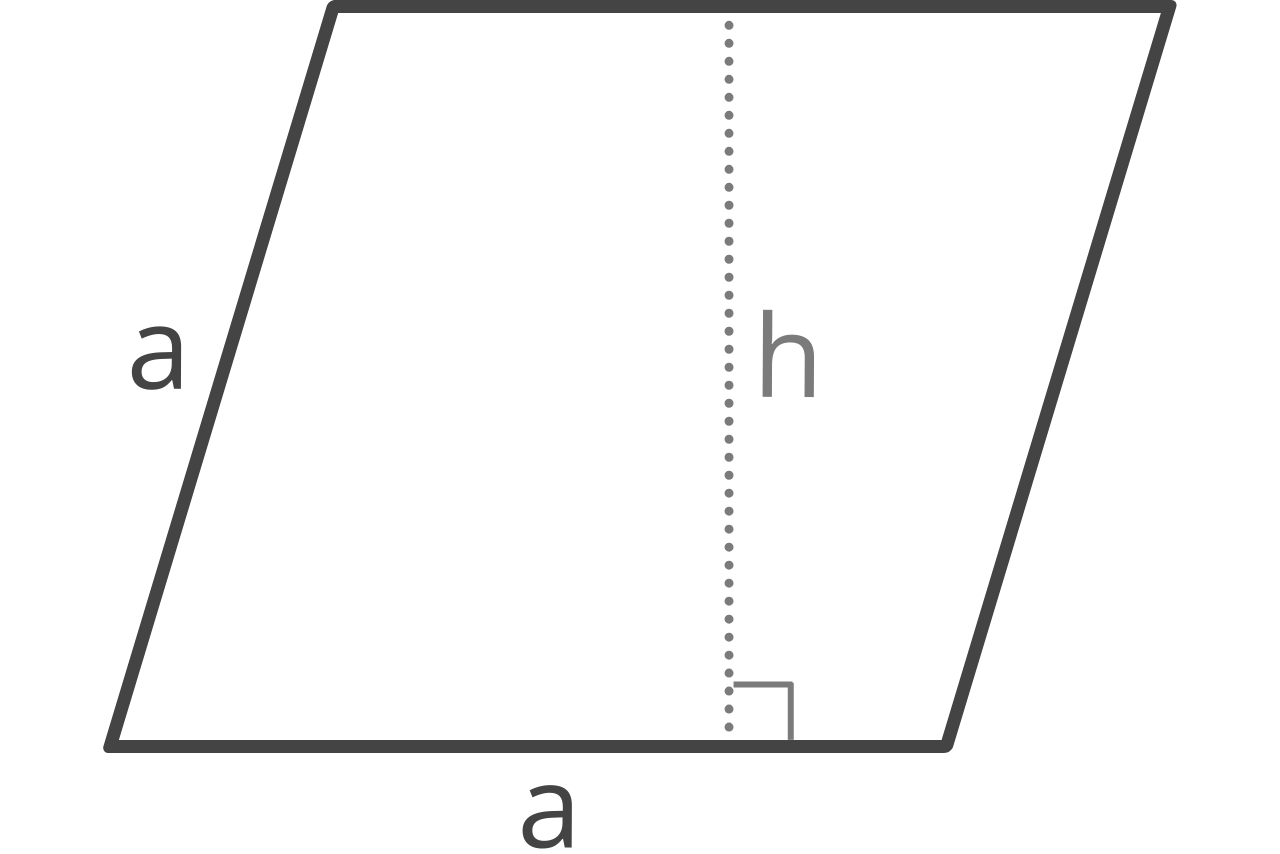
How to Find Area of a Rhombus
A rhombus is very similar to a parallelogram, but a rhombus has four sides of equal length. The interior angles of a rhombus are not right angles, but the lines connecting opposing angles intersect at a right angle.
The area of a rhombus is equal to the edge length times the height.
A = a × h
a = edge length
h = height
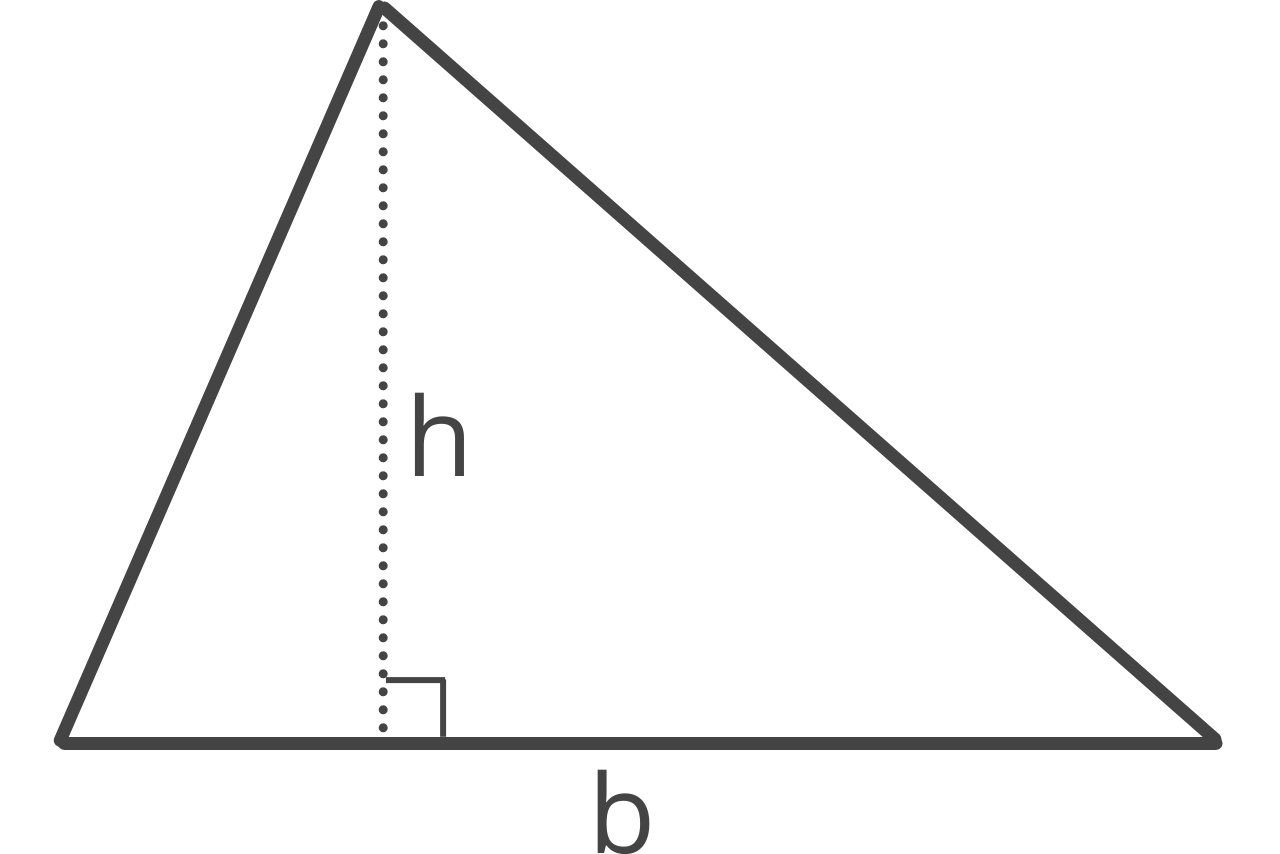
How to Find Area of a Triangle
A triangle is a polygon with three straight sides and three angles between the sides. There are six types of triangles: right, equilateral, isosceles, scalene, acute, and obtuse.
You can find the area of a triangle using several formulas, depending on the information you have about it. The most common formulas are BH, SSS, SAS, SSA, ASA, and AAS.
If you know the base and the height of a triangle, you can use the BH formula, which states that the area of a triangle is equal to one-half times the base times the height.
A = 1/2bh
b = base b
h = height
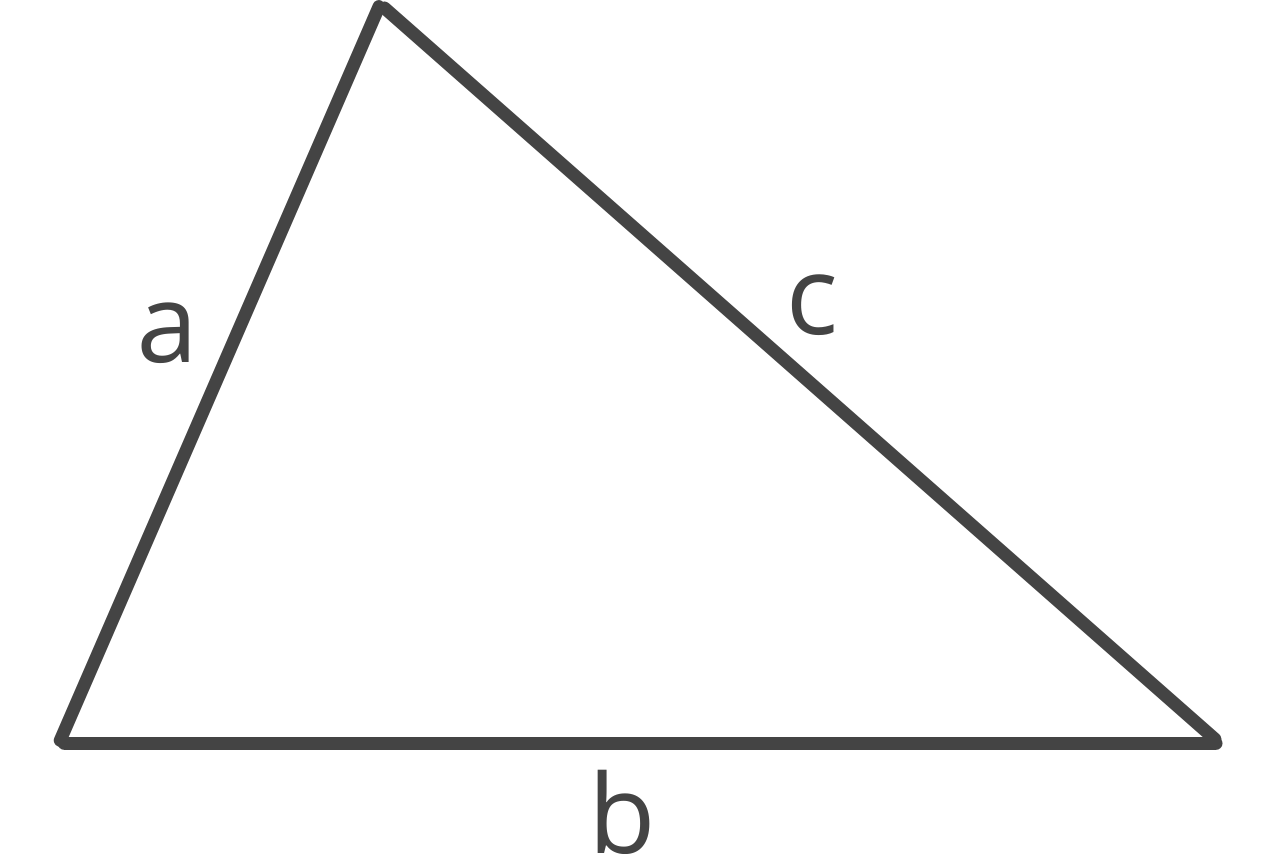
If you know the length of the three sides, you can use the SSS formula, also known as Heron’s formula, to find the area.
s = 1/2(a + b + c)
A = s(s – a)(s – b)(s – c))
a = side a
b = side b
c = side c
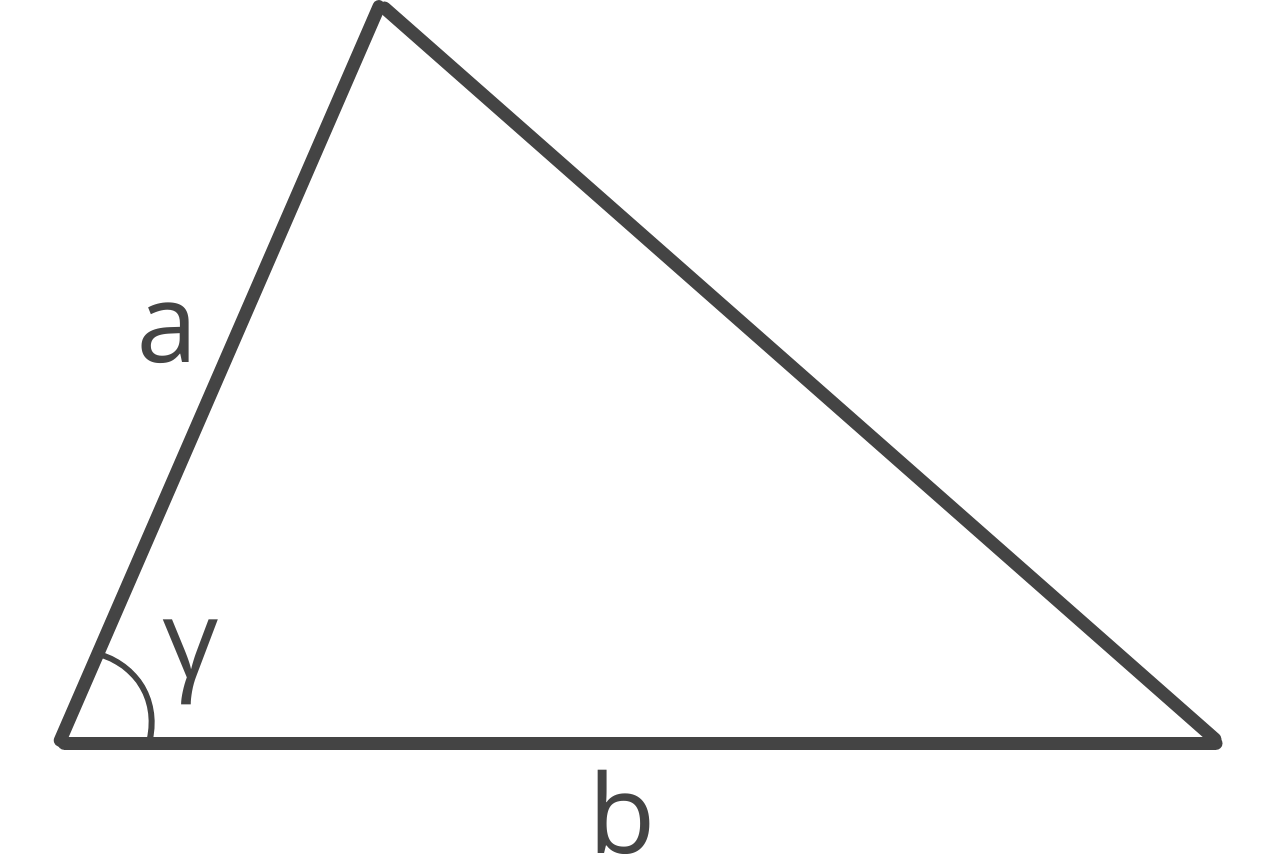
If you know the length of two sides and the connecting angle, then you can use the SAS formula to find the area.
A = ab ÷ 2 × sin(γ)
a = side a
b = side b
γ = angle
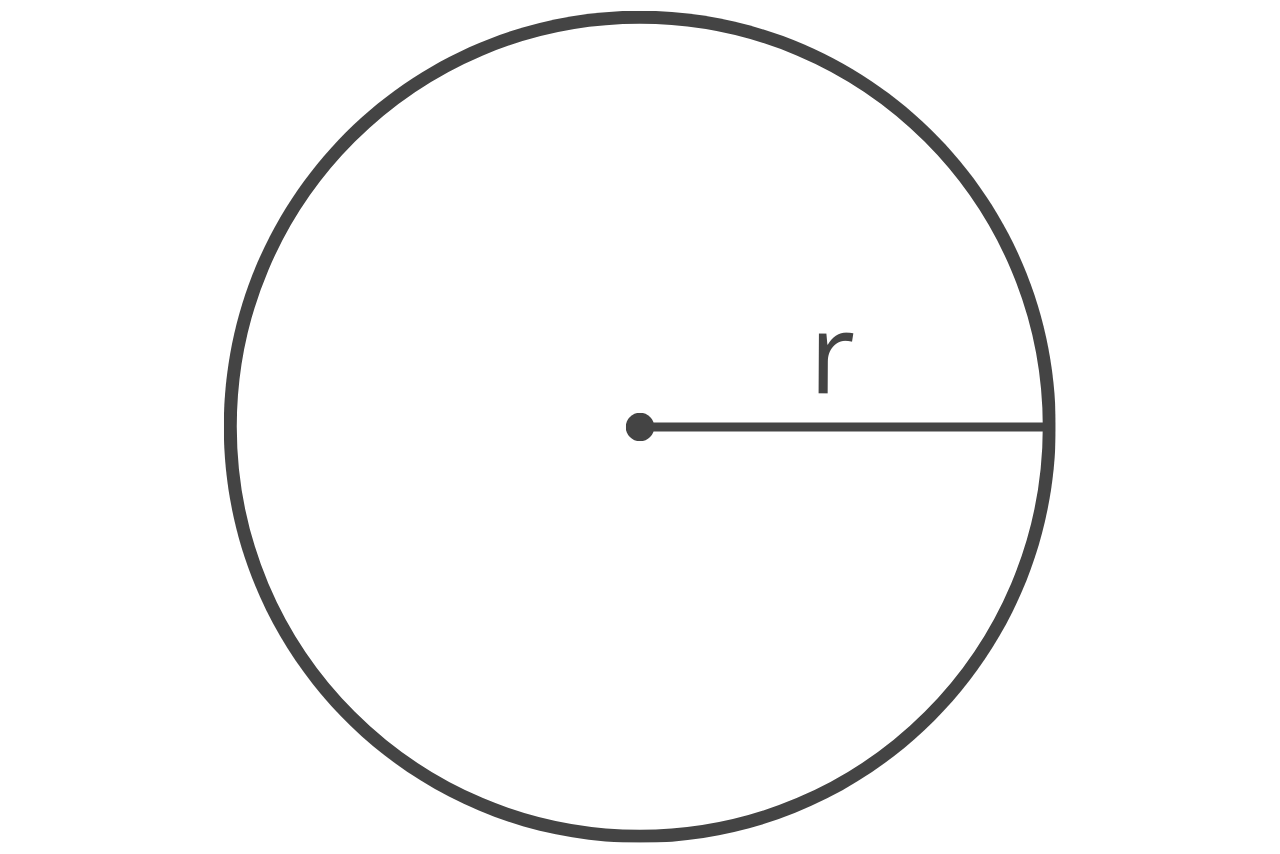
How to Find Area of a Circle
A circle is a round shape with no corners or edges. Each point along a circle is equidistant from the center. It’s important to note that a circle is a two dimensional shape, but it is not a polygon because it does not have straight sides.
The area of a circle is equal to π times the radius squared.
A = πr2
r = radius
If you know the circle’s diameter, you can find the radius by dividing the diameter in half.
A = π(d/2)2
d = diameter
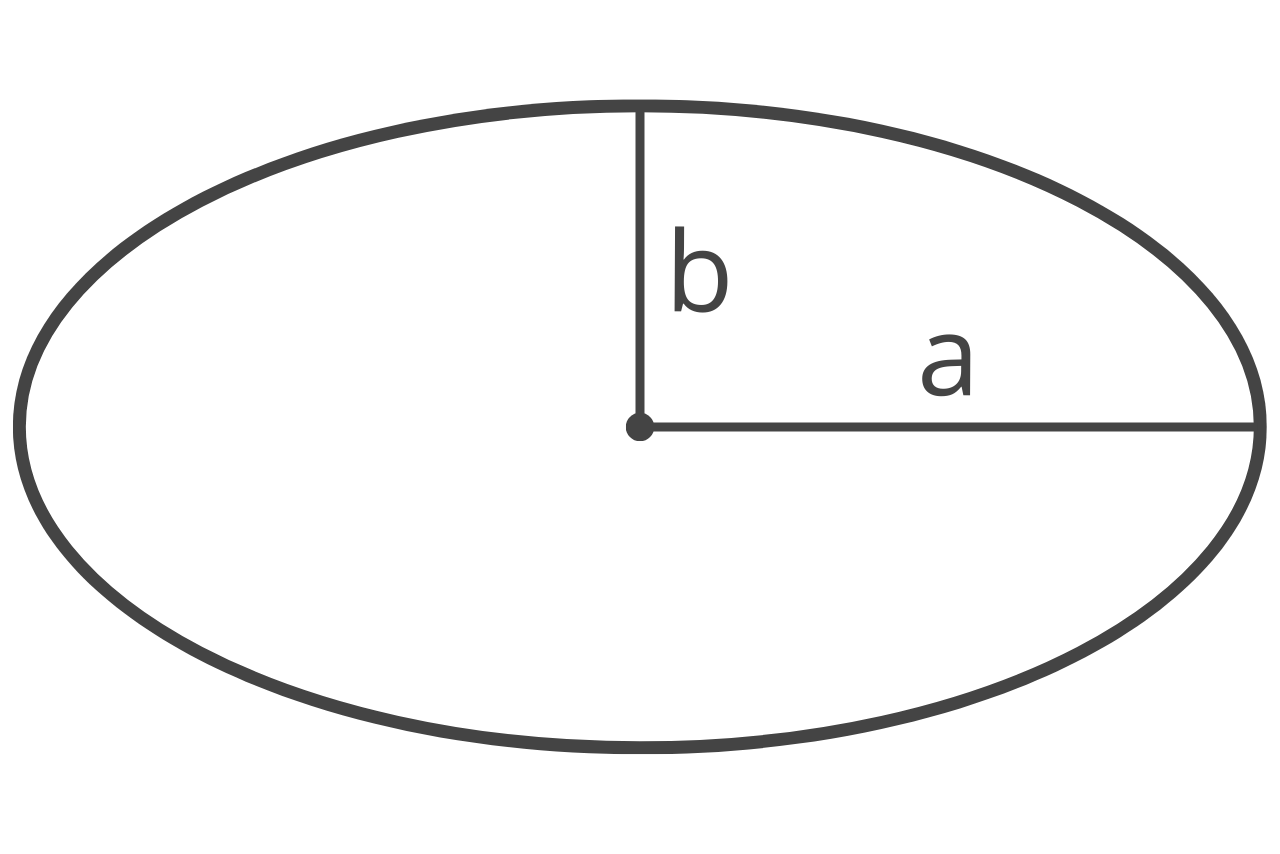
How to Find Area of an Ellipse
An ellipse, or oval, is a shape where the sum of the distances from two fixed points, called the foci, is constant. An ellipse has a diameter along the largest dimension, called the semi-major axis, and a smaller diameter, called the semi-minor axis.
It’s important to note that an ellipse is a two dimensional shape but it is not a polygon because it does not have any straight sides.
You can find the area of an ellipse by multiplying π times the radius of the semi-major axis times the radius of the semi-minor axis.
A = πab
a = semi-major axis a
b = semi-minor axis b
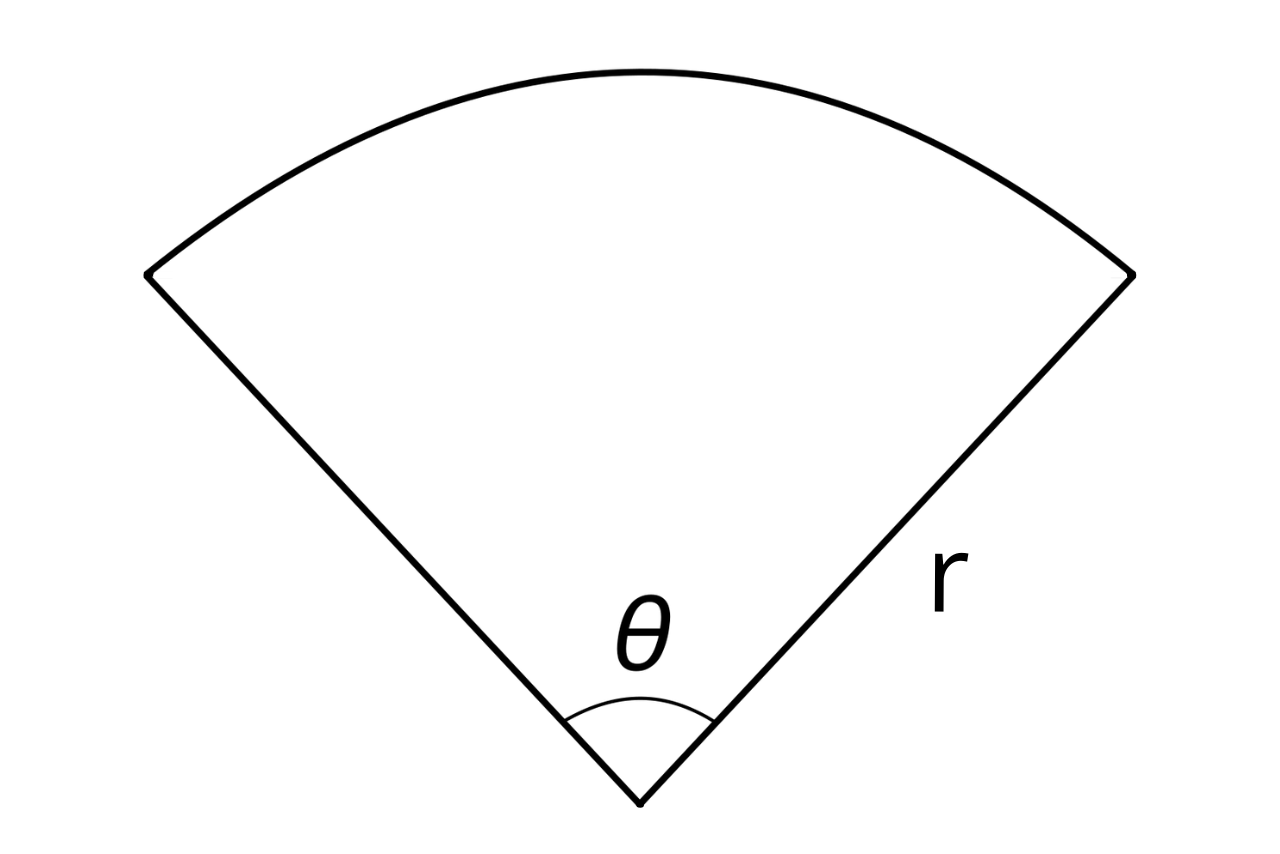
How to Find Area of a Sector
A sector is a pie-shaped piece of a circle consisting of an arc connecting a radius on either side. Just like a pie, a circle can be subdivided into various sectors.
The area of a sector is equal to the central angle divided by 360, times π times the radius squared.
A = (θ ÷ 360)πr2
r = radius
θ = angle in degrees
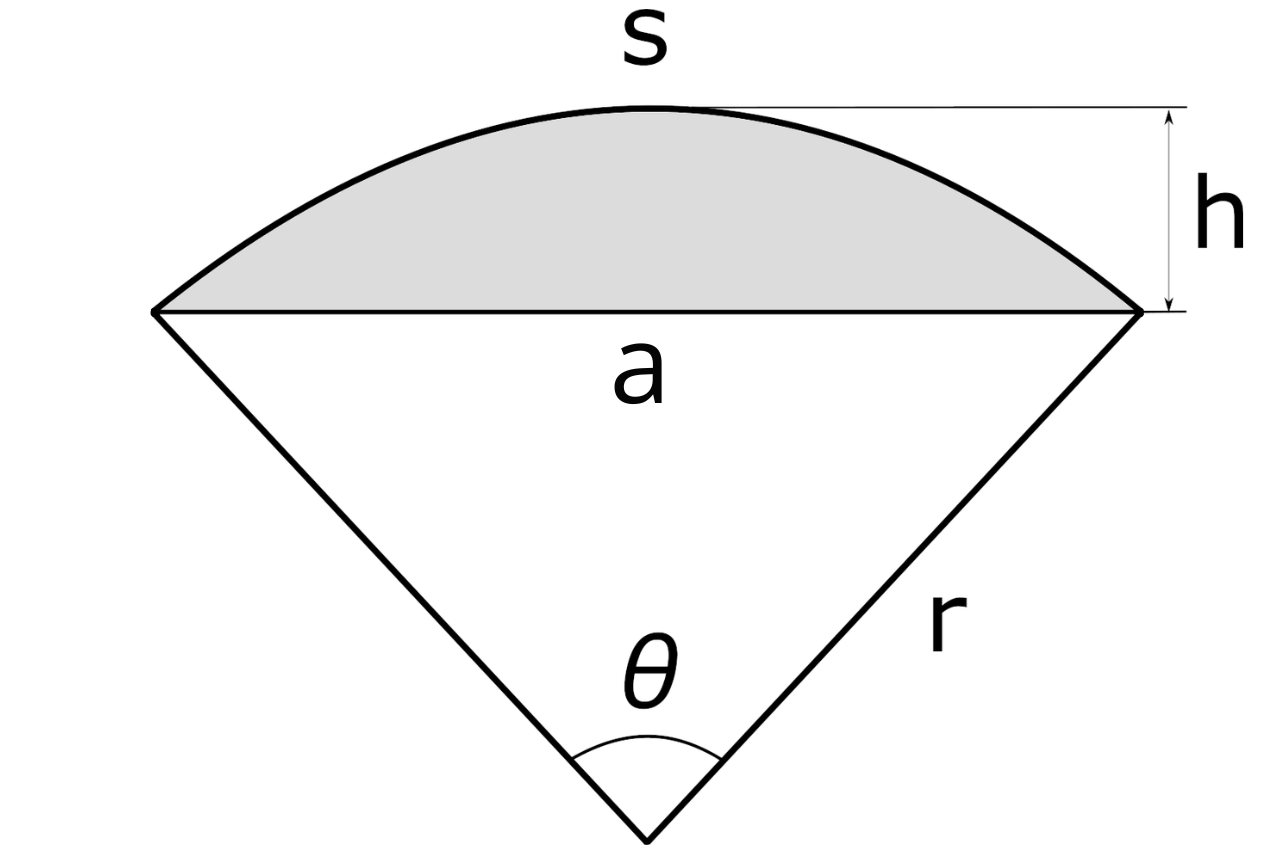
How to Find Area of a Segment
The segment of a circle is the region between the chord and arc connecting the endpoints of the chord. A chord is a line segment that connects any two points on a circle.
The segment would be the portion cut off of a sector if you sliced it at the point where the radius meets the arc on each side.
To find the area of a segment, multiply the radius squared by the central angle times π, divided by 360, minus the sine of the angle divided by 2.
A = (θ × π / 360 – sin(θ) / 2) × r²
r = radius
θ = angle in degrees
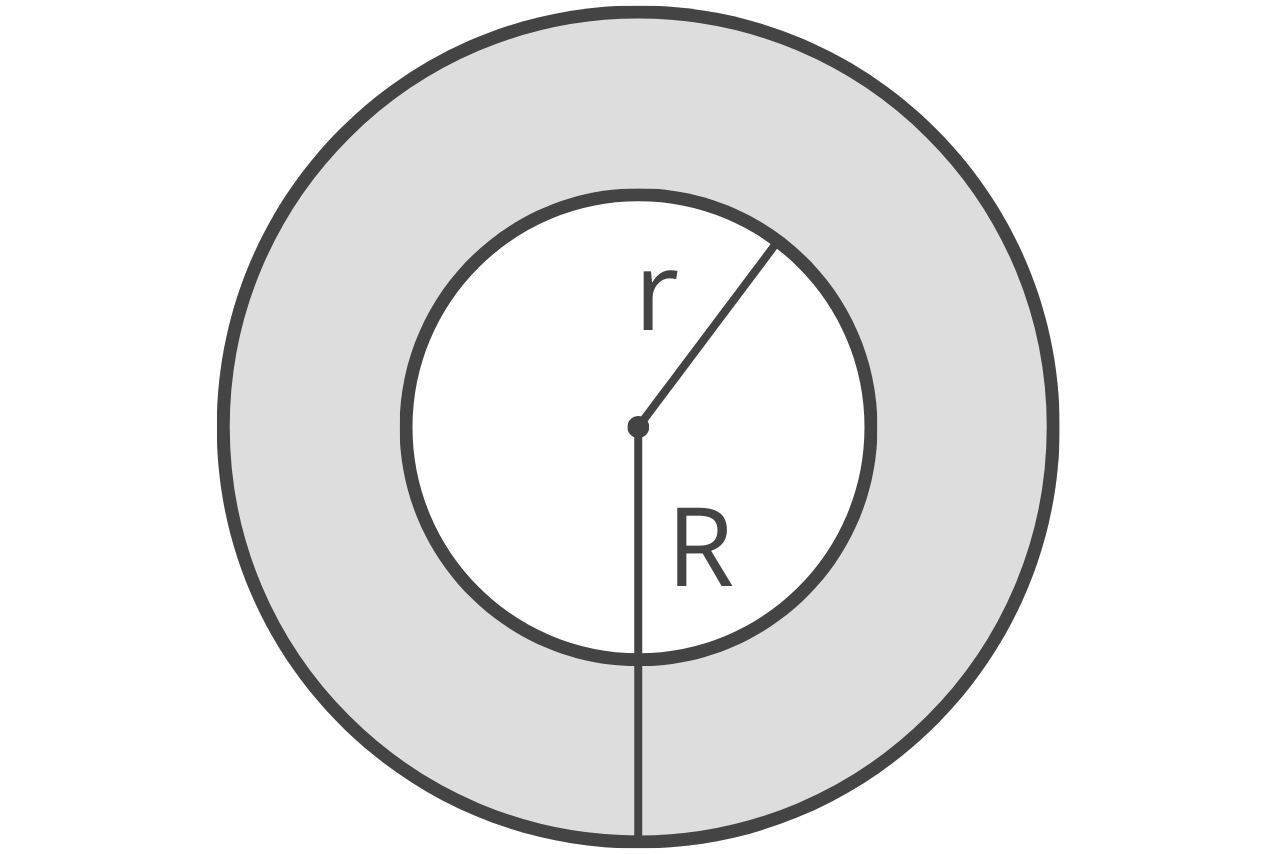
How to Find Area of a Ring
A circular ring, called an annulus, is a ring consisting of an inner circle and an outer circle. The area of the annulus is the space between these two circles.
You can find the area of an annulus by subtracting the area of the outer circle from the area of the inner circle. The formula is:
A = πR2 – πr2
R = larger radius
r = smaller radius
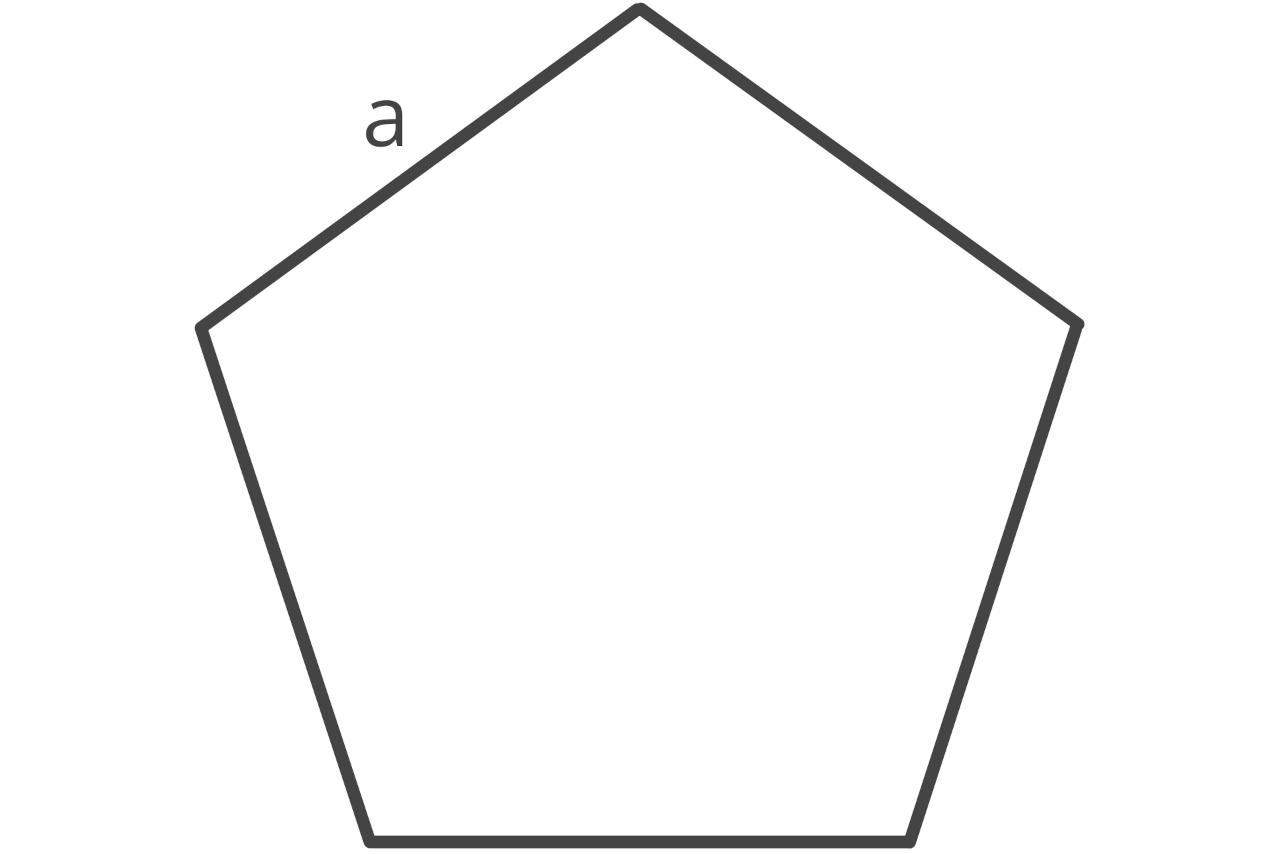
How to Find Area of a Pentagon
A pentagon is a regular polygon with five sides that are the same length. Each interior angle is also the same.
The area of a pentagon is equal to the side length squared times 5, divided by 4 times the tangent of π over 5.
A = (a2 × 5) ÷ (4 × tan(π ÷ 5))
a = edge length
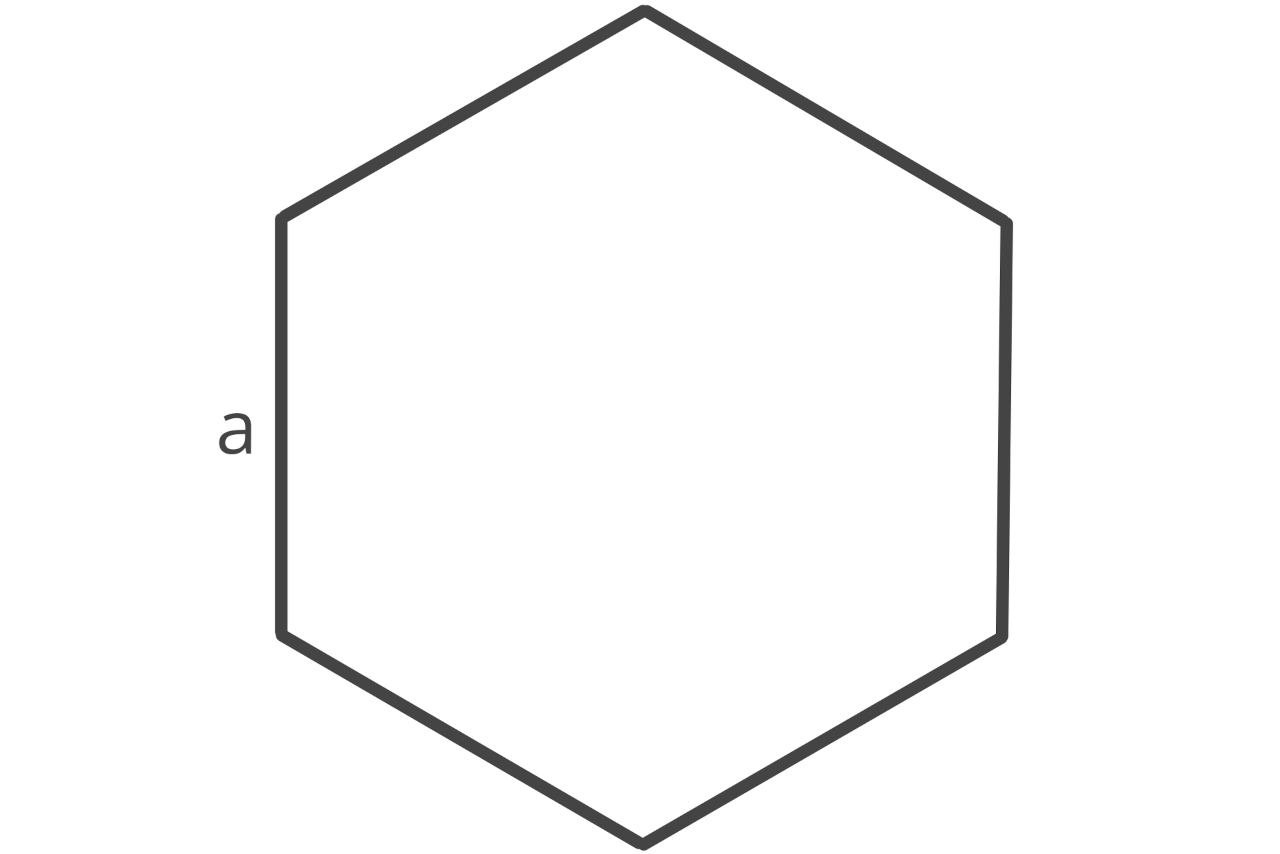
How to Find Area of a Hexagon
A hexagon is a six-sided regular polygon with equal sides and angles.
The area of a hexagon is equal to the side length squared times 6, divided by 4 times the tangent of π over 6.
A = (a2 × 6) ÷ (4 × tan(π ÷ 6))
a = edge length
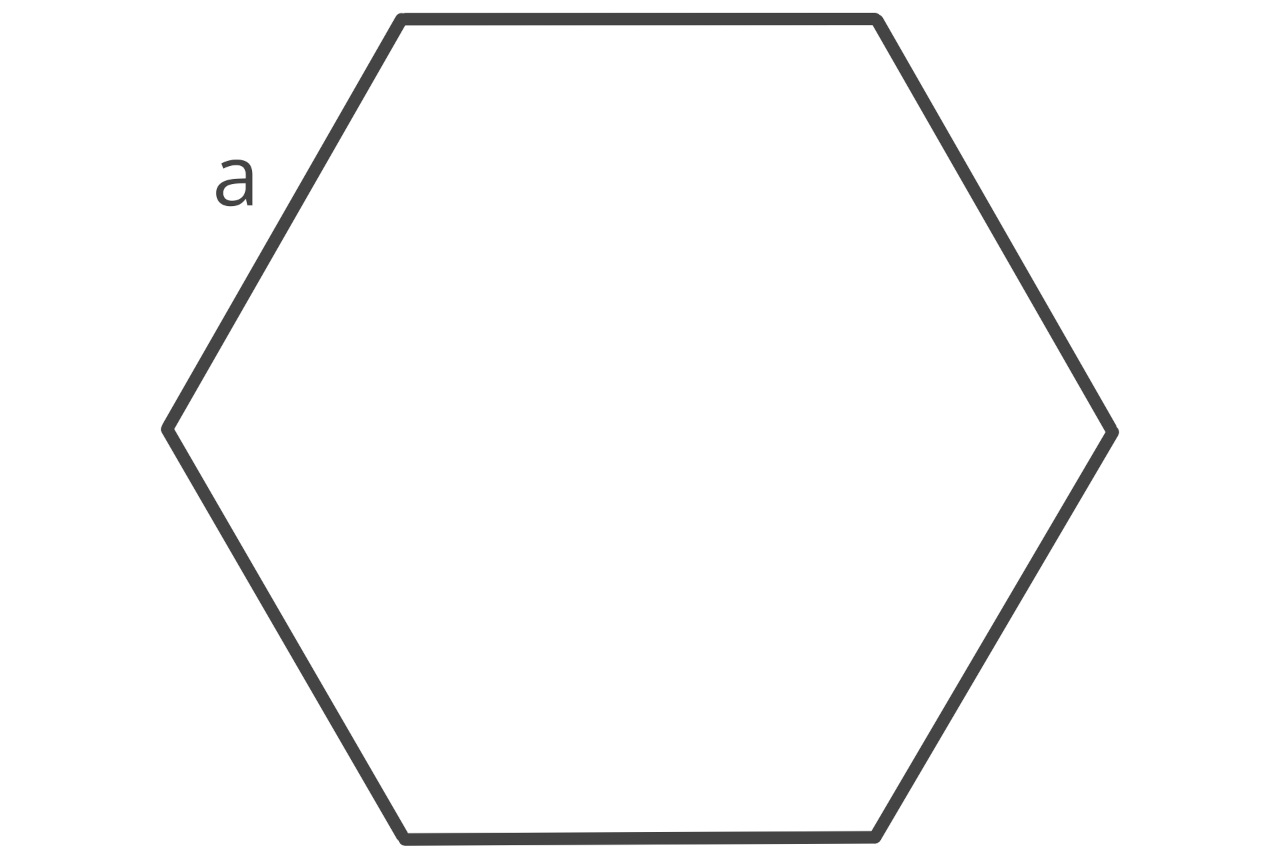
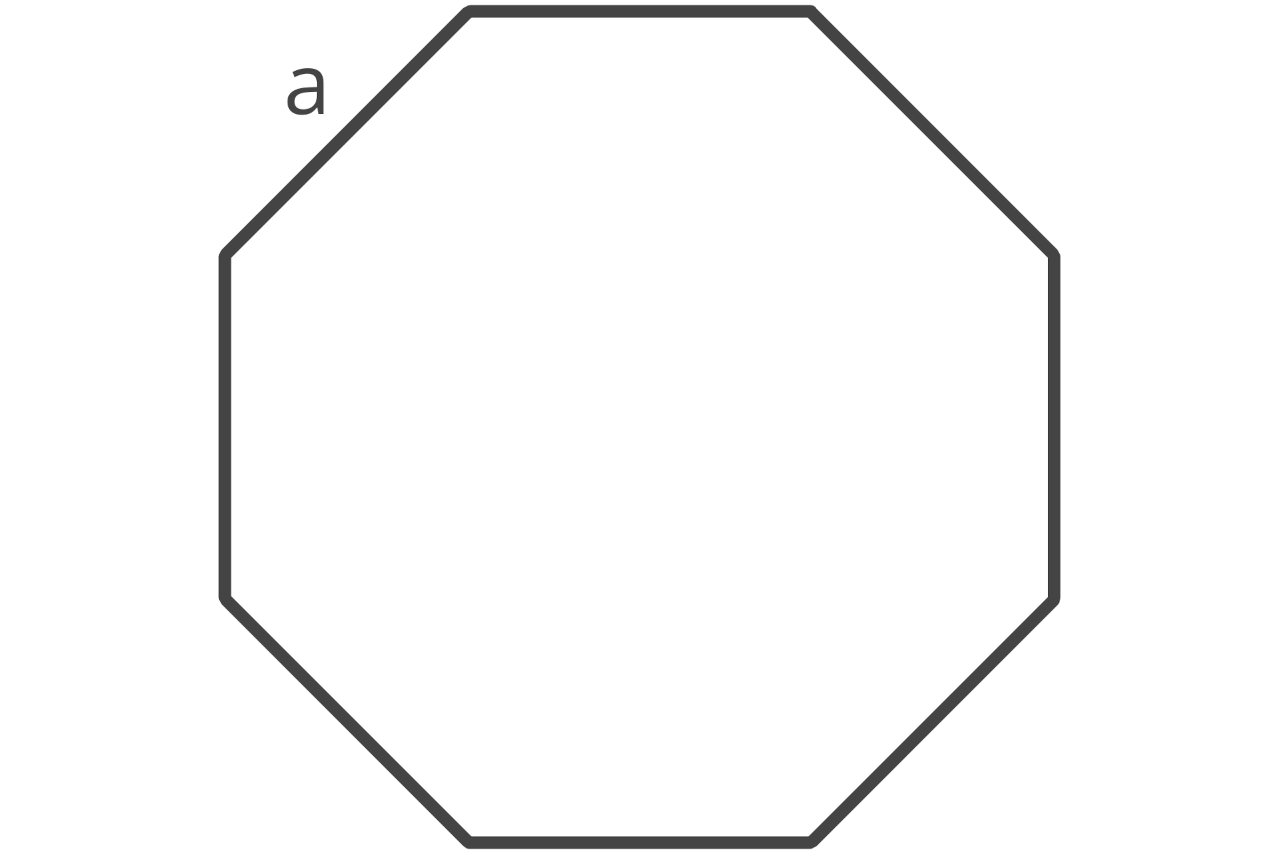
How to Find Area of an Octagon
An octagon is a regular polygon with eight sides that are the same length and eight interior angles that have equal degree measures.
The area of an octagon is equal to the side length squared times 8, divided by 4 times the tangent of π over 8.
A = (a2 × 8) ÷ (4 × tan(π ÷ 8))
a = edge length
How to Find Area of a Regular Polygon
A regular polygon is a shape with straight sides of equal length with interior angles that are also all the same. A square, pentagon, hexagon, and octagon are all examples of regular polygons.
The area of a polygon is equal to the side length squared times the number of sides, divided by 4 times the tangent of π divided by the number of sides.
A = (a2 × n) ÷ (4 × tan(π ÷ n))
a = edge length
n = number of sides
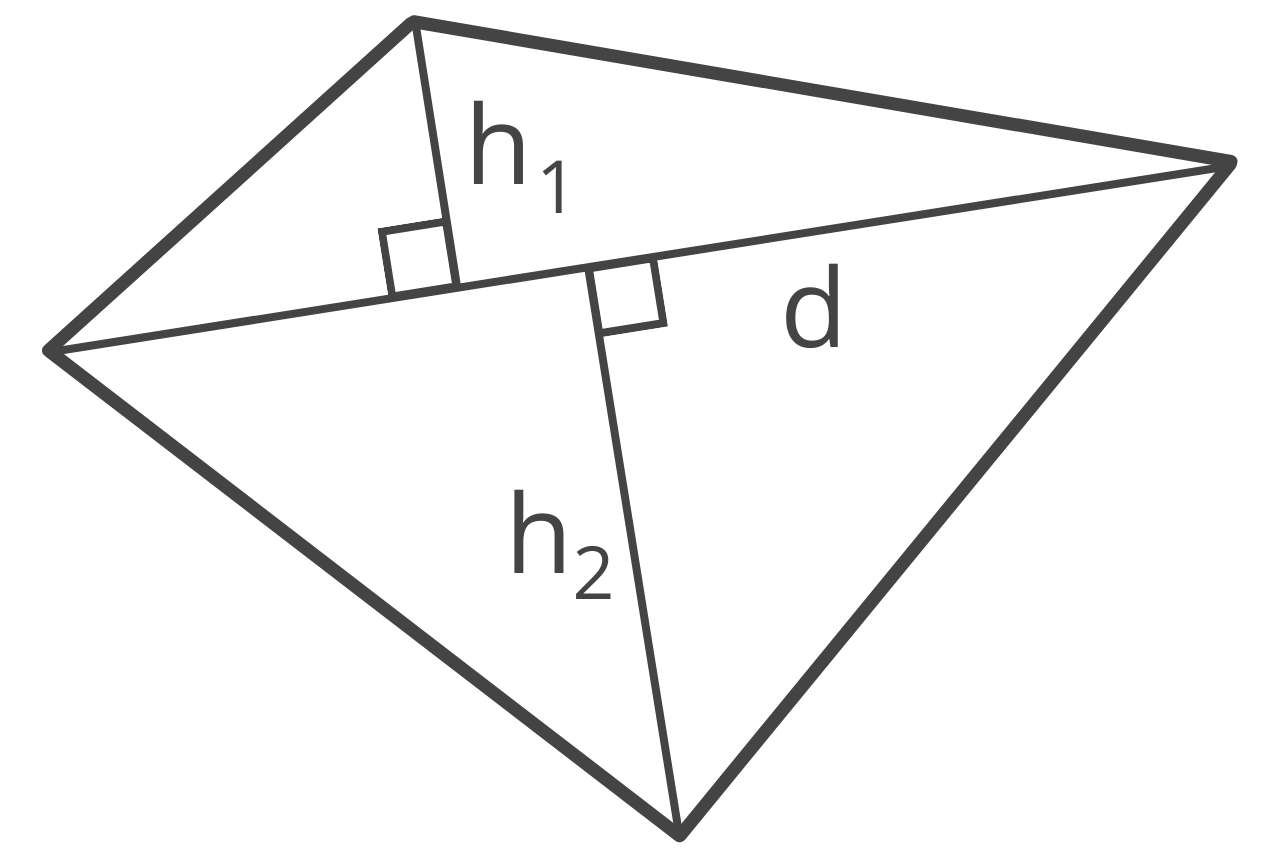
How to Find Area of an Irregular Quadrilateral
An irregular quadrilateral is a shape with four sides with different side lengths and different interior angles. The shape is not regular, and the angles that connect each side are not the same.
There are a few methods to find the area of an irregular quadrilateral. One way is to connect two opposing angles, then measure the distance of a perpendicular line that connects this line to the remaining two corners.
Then the area is equal to one-half of the length of the diagonal, times the sum of the two distances to the remaining corners.
A = 1/2 × d × (h1 + h2)
d = diagonal
h1 = height 1
h2 = height 2
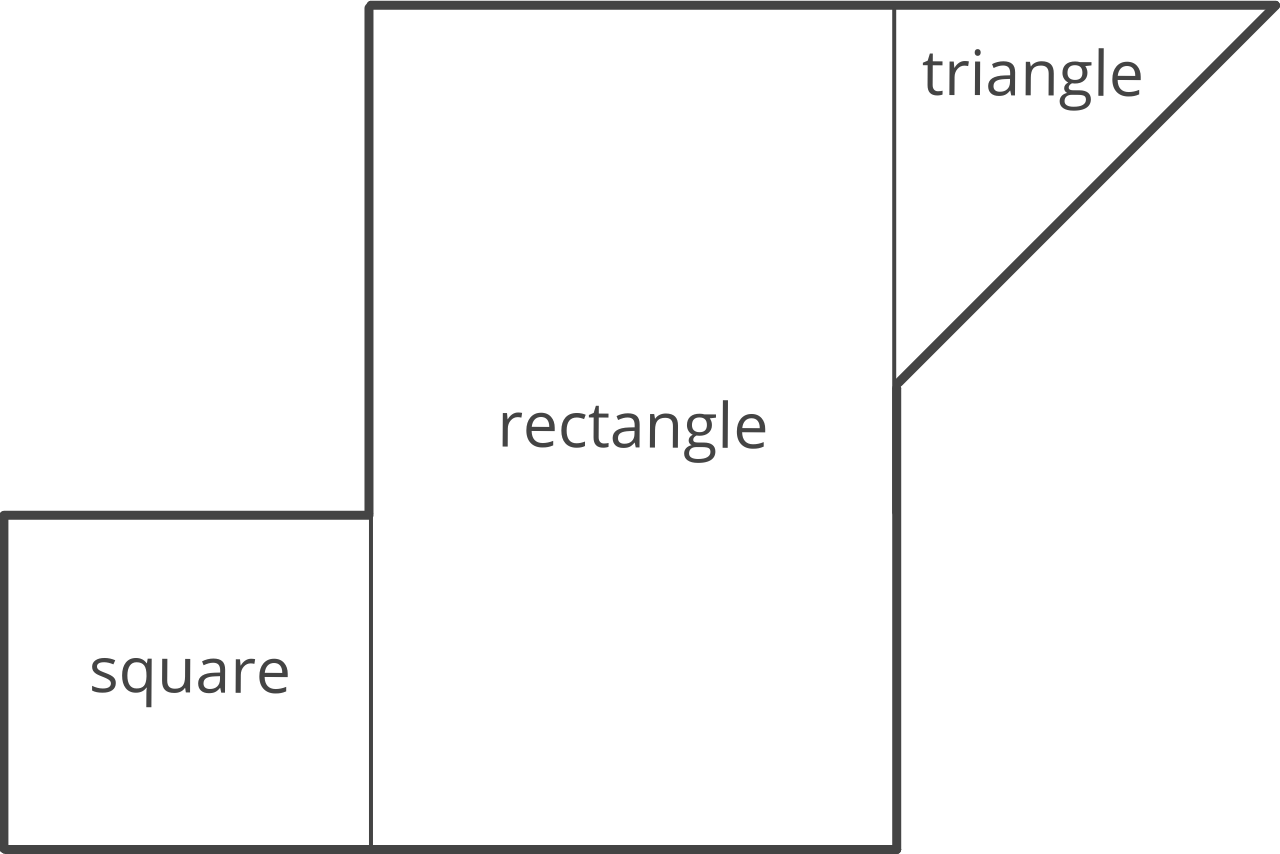
How to Find Area of a Compound Shape
A compound shape is a shape that is composed of other shapes and is not a regular polygon, circle, triangle, or quadrilateral.
The trick to finding the area of an irregular or complex shape is to break the shape up into regular polygons such as triangles and squares first, then find the area of those simpler shapes first, and then add them together to find the total.
Frequently Asked Questions
When should we calculate area?
Finding the area of a space is a skill that is frequently used outside of the classroom. For instance, when measuring for landscape mulch, flooring, paint, and even concrete patios, you’ll need to find the area of the space.
You should calculate the area whenever you need to know how large a space is.
How do you measure area?
To measure the area of a space, you need to find the right formula for the shape, then get the measurements needed for each variable in the formula.
- Measuring the required dimensions of the shape using a ruler or tape measure.
- Substitute the measurements for the variables in the area formula.
How do you calculate the area of a large space?
You can find the area of a really large space, such as a plot of land or a city, just like you would for a small shape and using the same formulas above. The difference is how you might measure the dimensions and the units used.
Large spaces are usually measured in acres, hectares, square miles, or square kilometers.
If you already know the dimensions of the space, simply plug them into one of the formulas above and solve. If you don’t have the dimensions yet, use a tool like our acreage calculator to measure using a map.
After you have the area, you might need to convert it to acres or square miles. For instance, if you have a measurement in square feet, you can convert it to acres by dividing the square feet by 43,560 to get the result.
What’s the difference between area and surface area?
While area is the size of a two-dimensional plane, surface area is the size of the surface of a three-dimensional solid shape. There are a few different types of surface area: curved surface area, lateral surface area, and total surface area.
- Curved surface area is a measure of the area of the curved regions of an object.
- Lateral surface area is the area of all of the faces of the object other than the top and bottom bases.
- Total surface area is the area of the entire object, including the curved surface, faces, and the base.
What’s the difference between area and perimeter?
Area and perimeter are related, but the perimeter is the distance around a two-dimensional shape, while area is the size of the shape itself.
The perimeter is a length measurement of the boundary around the shape. Imagine you have a rectangle shape; if you took a string and wrapped it around the rectangle, the perimeter would be the length of the string.
Of course, we have a perimeter calculator to help solve this length measurement.
Why is area squared?
Area is answered using squared units because we are multiplying a dimension times a dimension (length x width). You can think of it as squared means two and we are multiplying two sides.