Parallelogram Area Calculator
Calculate the area of a parallelogram using the base and height, sides and angle, or diagonals and angle with the calculator below.
Area:
On this page:
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
Pateakia has worked in education for 15 years and has three degrees, including a PhD, Master's degree, and Bachelor's degree. She specializes in mathematics.
How to Calculate the Area of a Parallelogram
A parallelogram is a four-sided figure with opposite sides that are parallel. Whether you’re doing homework, landscaping, or engaging in any project that requires an understanding of geometrical calculations, knowing how to calculate the area of a parallelogram is invaluable.
There are several ways to calculate the area of a parallelogram, depending on the information you have.
How to Calculate Area Using Base and Height
The most common method to find the area of a parallelogram is by using its base and height.
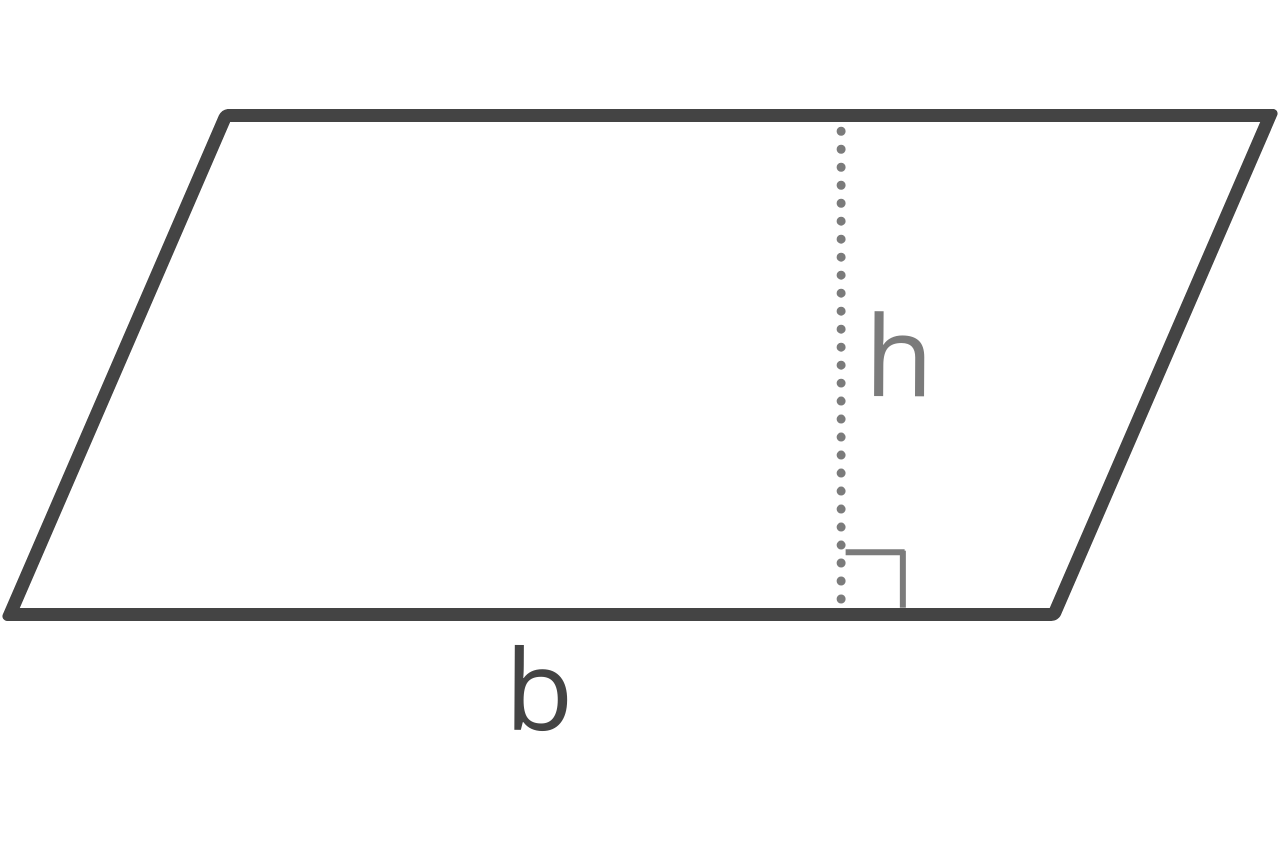
The parallelogram area formula is:
A = b × h
The area A of a parallelogram is equal to the length of the base b times the height h.
For example, let’s calculate the area of a parallelogram with a base of 5 and a height of 6.
A = 5 × 6 = 30
This parallelogram has an area of 30.
How to Calculate Area Using the Sides and Interior Angle
When you know the length of the sides, base, and the angle between them, you can calculate the area of a parallelogram using trigonometry.
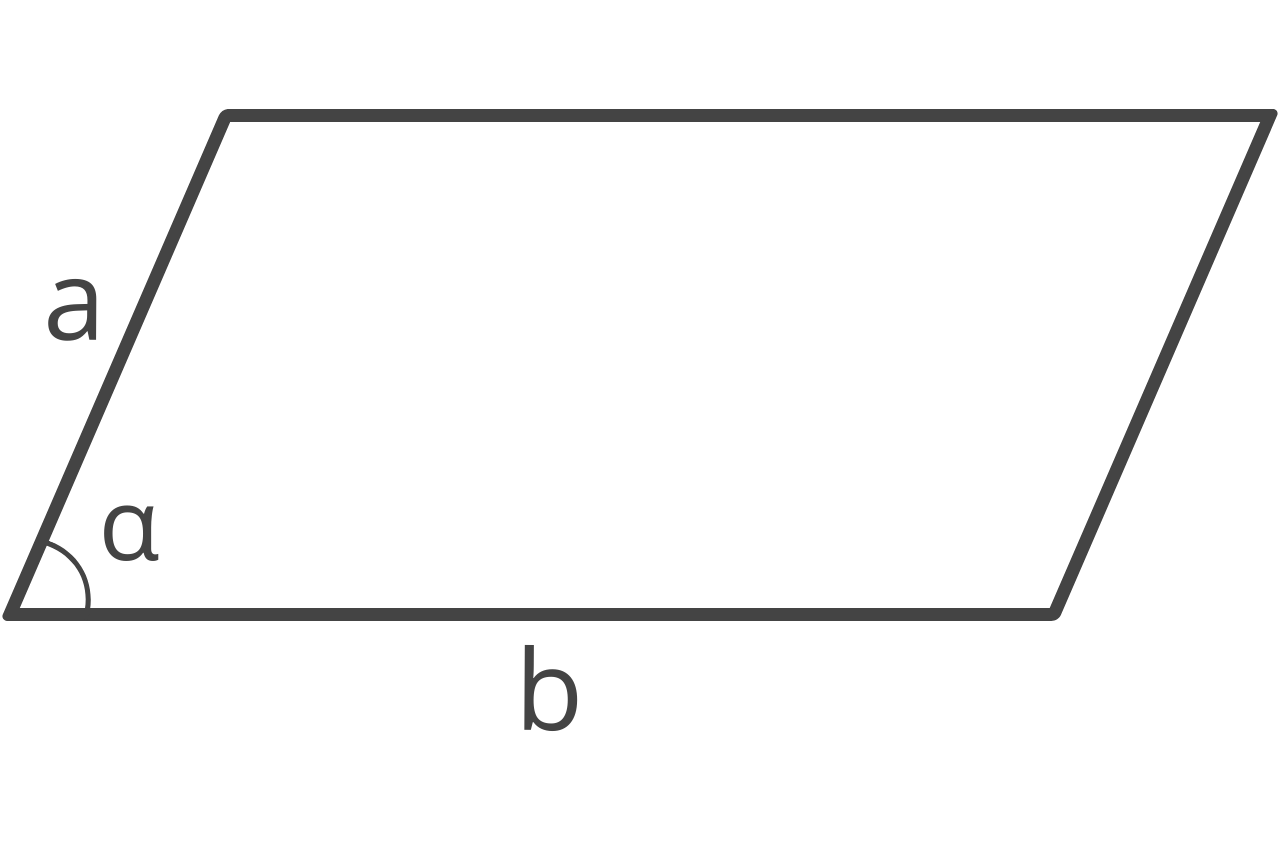
The formula to calculate the area of a parallelogram using the sides, base, and angle is:
A = a × b × sin(α)
The area A of a parallelogram is equal to the length of the side a times the length of the base b times the sine of angle α.
For example, let’s calculate the area of a parallelogram with a side of 7, a base of 8, and an interior angle of 60 degrees.
A = 7 × 8 × sin(60°) = 48.5
So, this parallelogram has an area of 48.5.
How to Calculate Area Using the Diagonals and Angle Between
If you know the lengths of the two diagonals that bisect the parallelogram and the angle between them, then you can find the area of the parallelogram using a formula:
A = ½ × c × d × sin(θ)
The area A of a parallelogram is equal to the length of the diagonal c times the length of the diagonal d times the sine of angle θ.
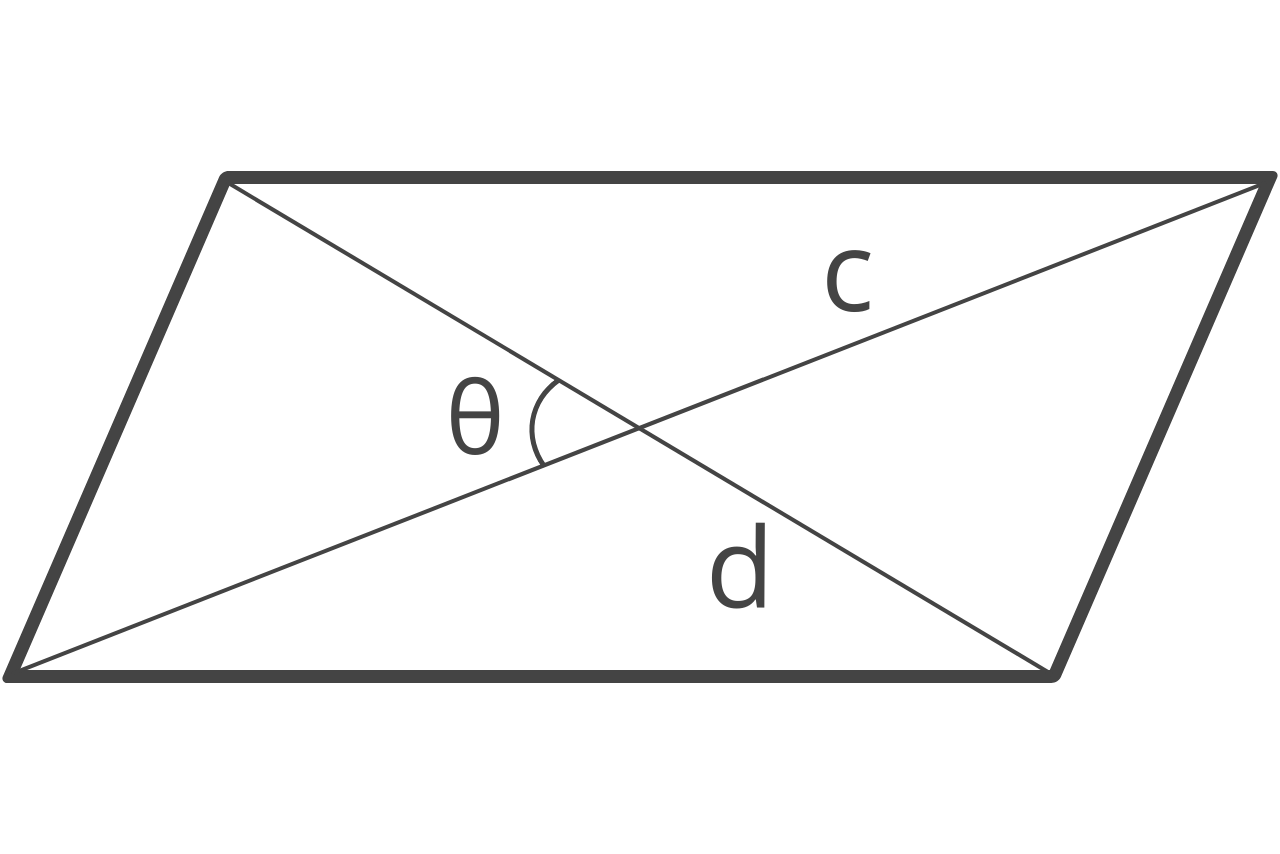
For example, let’s calculate the area of a parallelogram with diagonals of 9 and 12 and an interior angle of 30 degrees.
A = ½ × 9 × 12 × sin(30°) = 27
So, this parallelogram has an area of 27.
You may also find our trapezoid area calculator useful.