Trigonometry Calculator
Solve the sine, cosine, tangent, cotangent, secant, and cosecant of an angle using the trigonometric functions calculator below.
Solution:
| sin(θ): | |
|---|---|
| cos(θ): | |
| tan(θ): | |
| cot(θ): | |
| sec(θ): | |
| csc(θ): |
On this page:
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
Bailey is an experienced educator and specializes in K-12 math and science. She holds a Master's degree in professional education and holds several teaching certifications.
What is Trigonometry?
Trigonometry is a branch of mathematics used to explain the association between the angles and side lengths of triangles. While trigonometry covers a lot of ground, the primary concepts revolve around defining and solving the properties of right triangles and the relationships between the lengths of sides and the angles between them.
The major functions of trigonometry are sine, cosine, tangent, secant, cosecant, and cotangent. These functions define the distances of triangles for a given angle using the unit circle, as shown in the diagram below.
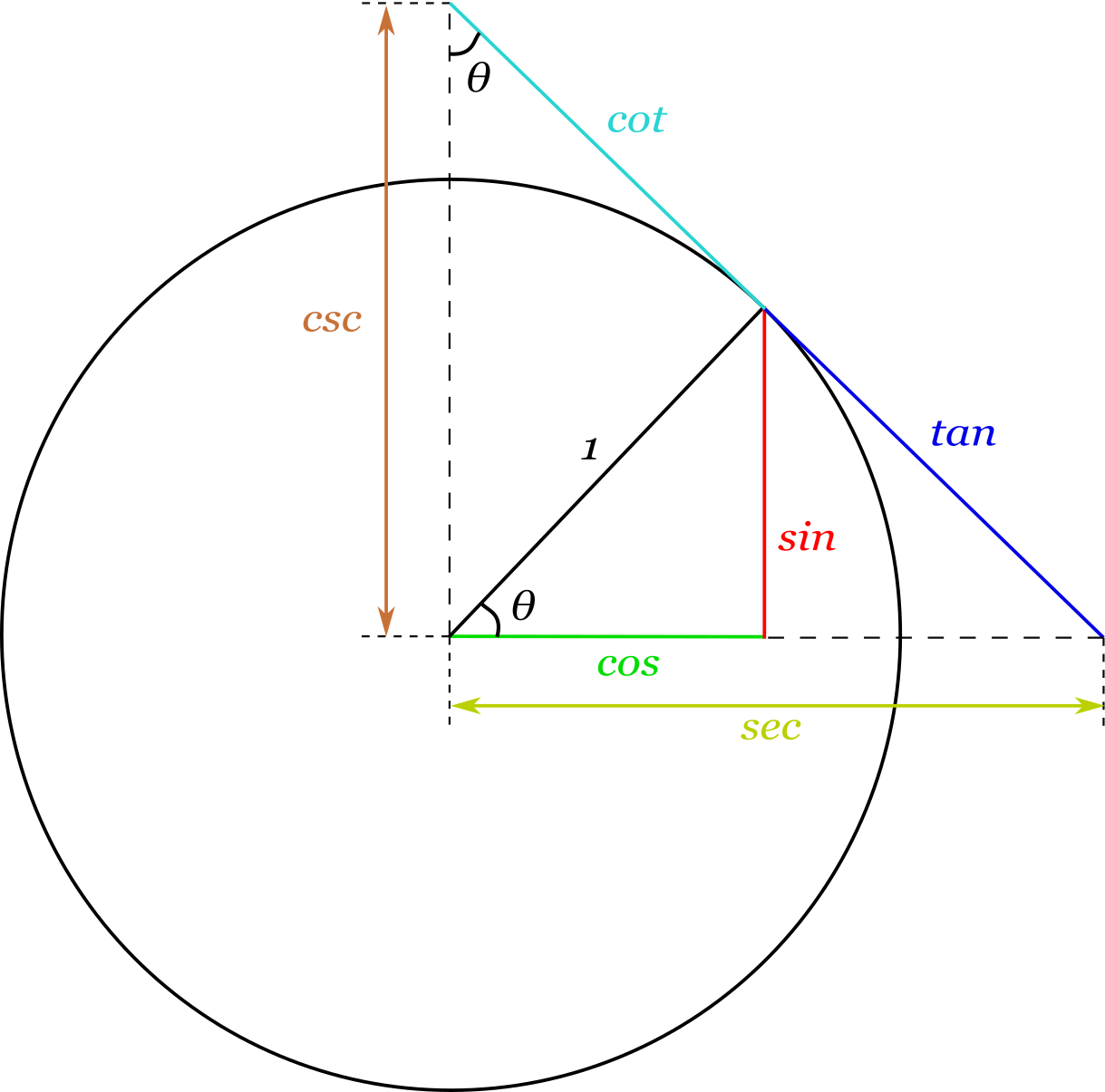
How to find sin, cos, tan, cot, sec, & csc
The major functions used in trigonometry are each abbreviated with three letters. The table below shows the primary trigonometric functions and their abbreviations.
| Function | Abbreviation |
|---|---|
| Sine | sin |
| Cosine | cos |
| Tangent | tan |
| Cosecant | csc |
| Secant | sec |
| Cotangent | cot |
The first three trigonometric functions define the relationship between the angles of a right triangle and its sides. The table below shows the definitions of each of the three primary functions.
| Sine | sin(θ) = opposite / hypotenuse |
| Cosine | cos(θ) = adjacent / hypotenuse |
| Tangent | tan(θ) = opposite / adjacent |
The second three trigonometric functions are the reciprocal of the primary functions. The table below shows their equations.
| Cosecant | csc(θ) = hypotenuse / opposite | csc(θ) = 1 / sin(θ) |
| Secant | sec(θ) = hypotenuse / adjacent | sec(θ) = 1 / cos(θ) |
| Cotangent | cot(θ) = adjacent / opposite | cot(θ) = 1 / tan(θ) |
The calculator above will solve all six properties given an angle in degrees or radians.
Frequently Asked Questions
Do you use degrees or radians in trigonometry?
You actually use both! Depending on the context, degrees or radians could be used. If you need help converting between degrees and radians, check out our conversion calculator.
Can you do trigonometry without a calculator?
It depends on the problem. If you are only finding the ratio, you do not need a calculator! Use the trigonometric ratios above. However, if you need to calculate the side length or a measurement of an angle, you may need to use a calculator.
Can you use trigonometry to find the area of a triangle?
Yes, you can use trigonometry to find as much information as possible about the sides and interior angles, then using that information, you can use an area formula such as the side-angle-side formula:
area = 1 / 2ab × sin(γ)
Where a and b are the lengths of two sides of the triangle and γ is the angle between them.
You can also use our triangle area calculator to solve this.
How do you know which trigonometric ratio to use?
It depends on the information you are given. From the right triangle, determine if you have the lengths of the opposite, adjacent, or hypotenuse. Match the side lengths that you have with the corresponding trigonometric function.
When will I use trigonometry in the real world?
Trigonometry has a wide range of real-life applications across various fields such as science, engineering, and architecture.
It is used to calculate distances and bearings in navigation, analyze forces in physics, design structures in engineering, and create 3D images in medical imaging. Additionally, trigonometry plays a crucial role in computer graphics, astronomy, music theory, and robotics.
Helpful Trigonometry Tips
These are some tips to help with using the trigonometric functions.
Use SOHCAHTOA
SOHCAHTOA is an acronym to help remember the three primary trigonometric functions. Each letter corresponds with the first letter of the word in the trigonometric ratio.
Sin(θ) = Opposite/Hypotenuse
Cos(θ) = Adjacent/Hypotenuse
Tan(θ) = Opposite/Adjacent
You can use our SOHCAHTOA calculator to calculate any side or angle in a right triangle using these formulas.
Use the Pythagorean Theorem
For right triangles, remember that the Pythagorean Theorem can be used if you know two sides of the right triangle. The Pythagorean Theorem states:
a² + b² = c²
Where a and b are the length of the short sides, and c is the length of the hypotenuse.
You can learn more about how to use the theorem on our Pythagorean Theorem calculator.
Remember the Hypotenuse, Opposite, and Adjacent Sides of a Right Triangle
Identifying the hypotenuse, opposite, and adjacent sides of the right triangle is essential to using the trigonometric functions to solve for the triangle’s properties.
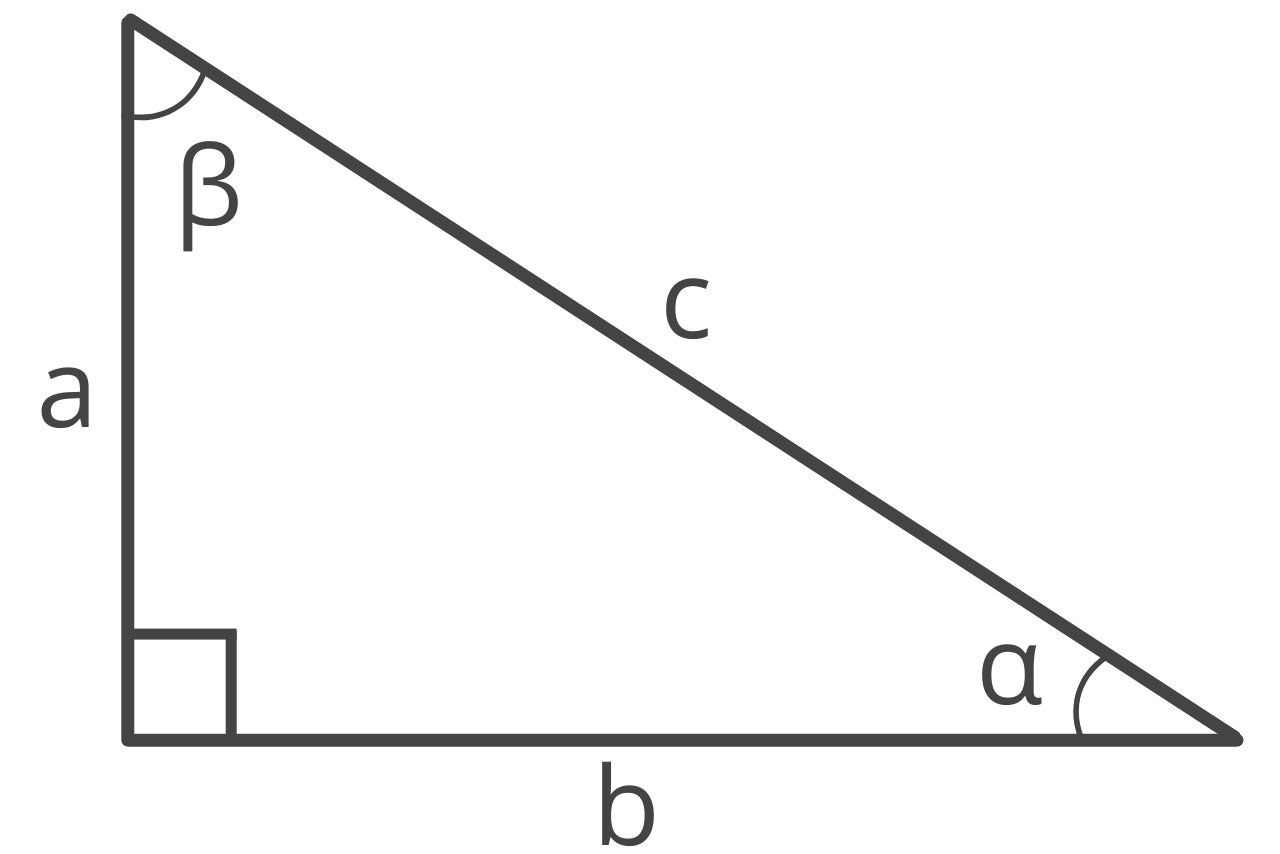
Right triangles are composed of two legs and a hypotenuse.
Hypotenuse: The hypotenuse is the longest side of a right triangle and is always opposite the 90° right angle.
The opposite and adjacent sides are the legs (shorter sides) of the right triangle and depend on the angle of reference.
Opposite: The leg of the right triangle that does not touch the angle of reference.
Adjacent: The leg of the right triangle that touches the angle of reference and is not the hypotenuse.
In the right triangle above, the opposite side of α is a, the adjacent side of α is b, and the hypotenuse is c.