Hypotenuse Calculator
Calculate the length of the hypotenuse in a right triangle using two sides or one side and one angle with the calculator below.
Hypotenuse:
On this page:
- Calculator
- How to Find the Hypotenuse of a Right Triangle
- Formula One: Given Two Legs
- Formula Two: Given One Leg and the Adjacent Angle
- Formula Three: Given One Leg and the Opposite Angle
- Formula Four: Given One Leg and the Area
- How to Find the Hypotenuse for a 45 45 90 Right Triangle
- How to Find the Hypotenuse for a 30 60 90 Right Triangle
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
Zach is a former math teacher with a Master's degree in education and a Bachelor's degree in mathematics, and is currently pursuing his PhD.
How to Find the Hypotenuse of a Right Triangle
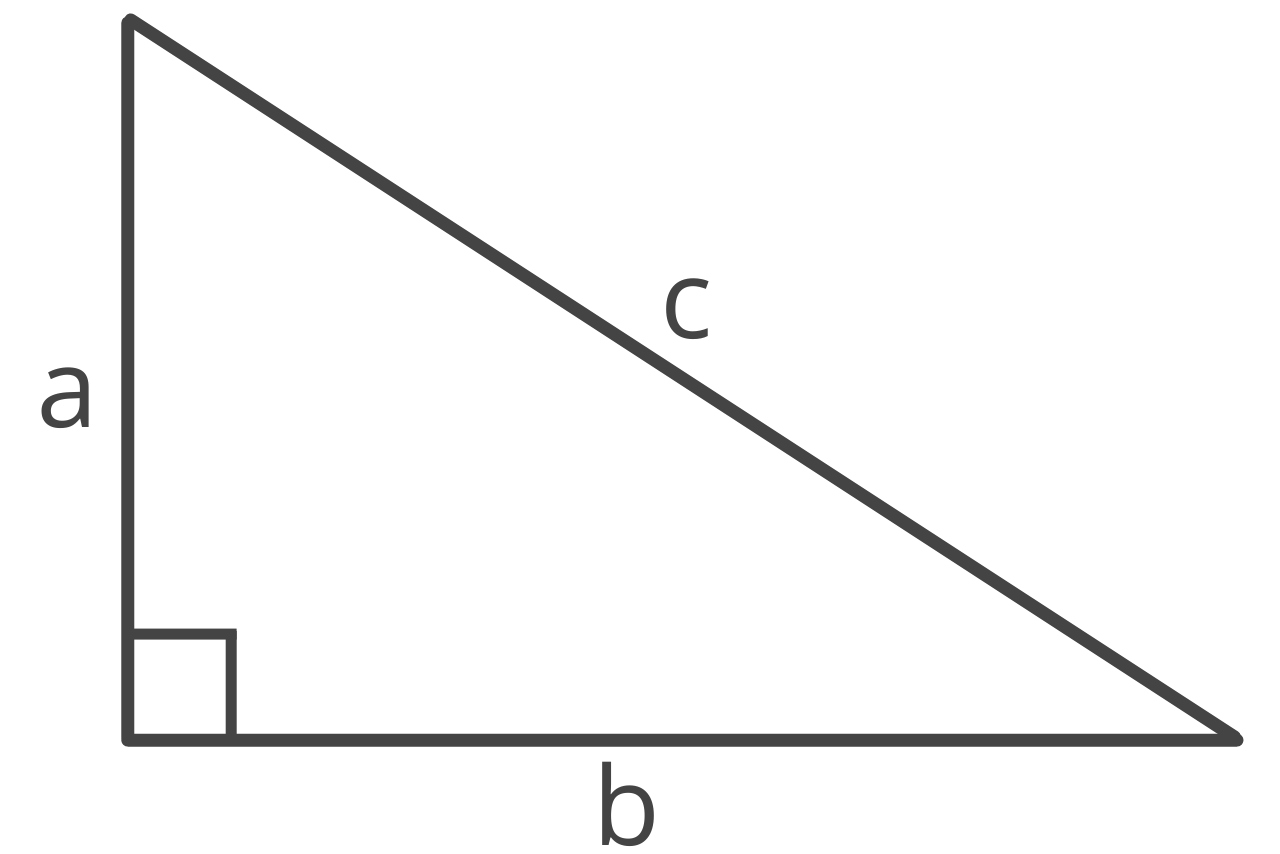
The hypotenuse is the longest side of a right triangle and is always opposite the 90° right angle.
The illustration below is a right triangle. The hypotenuse is labeled as c, and the opposite 90° angle is typically symbolized with the square drawn at the vertex.
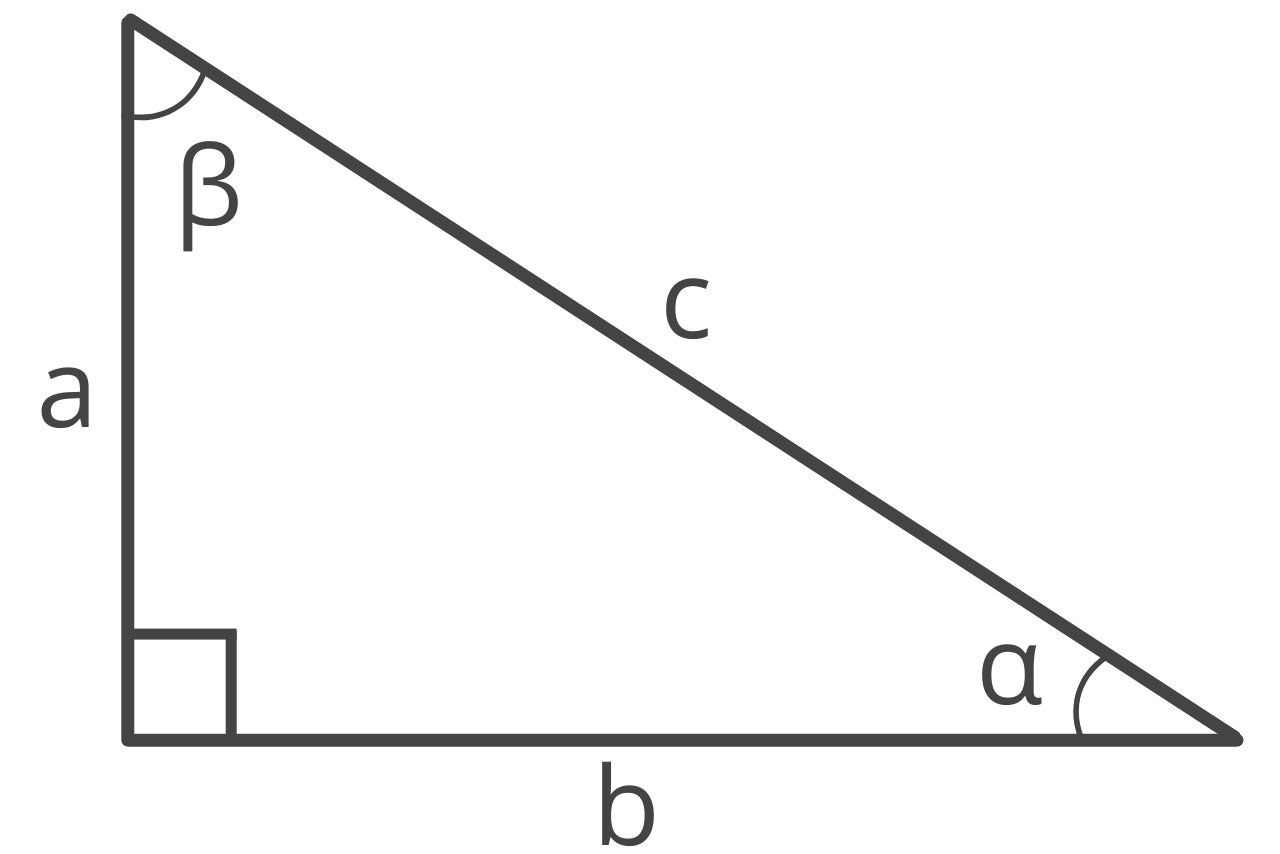
The two shorter side lengths (often called the legs of a right triangle), are labeled as a & b, and are opposite the interior angles labeled α & β.
You can solve the hypotenuse using a little trigonometry and one of the following formulas.
Formula One: Given Two Legs
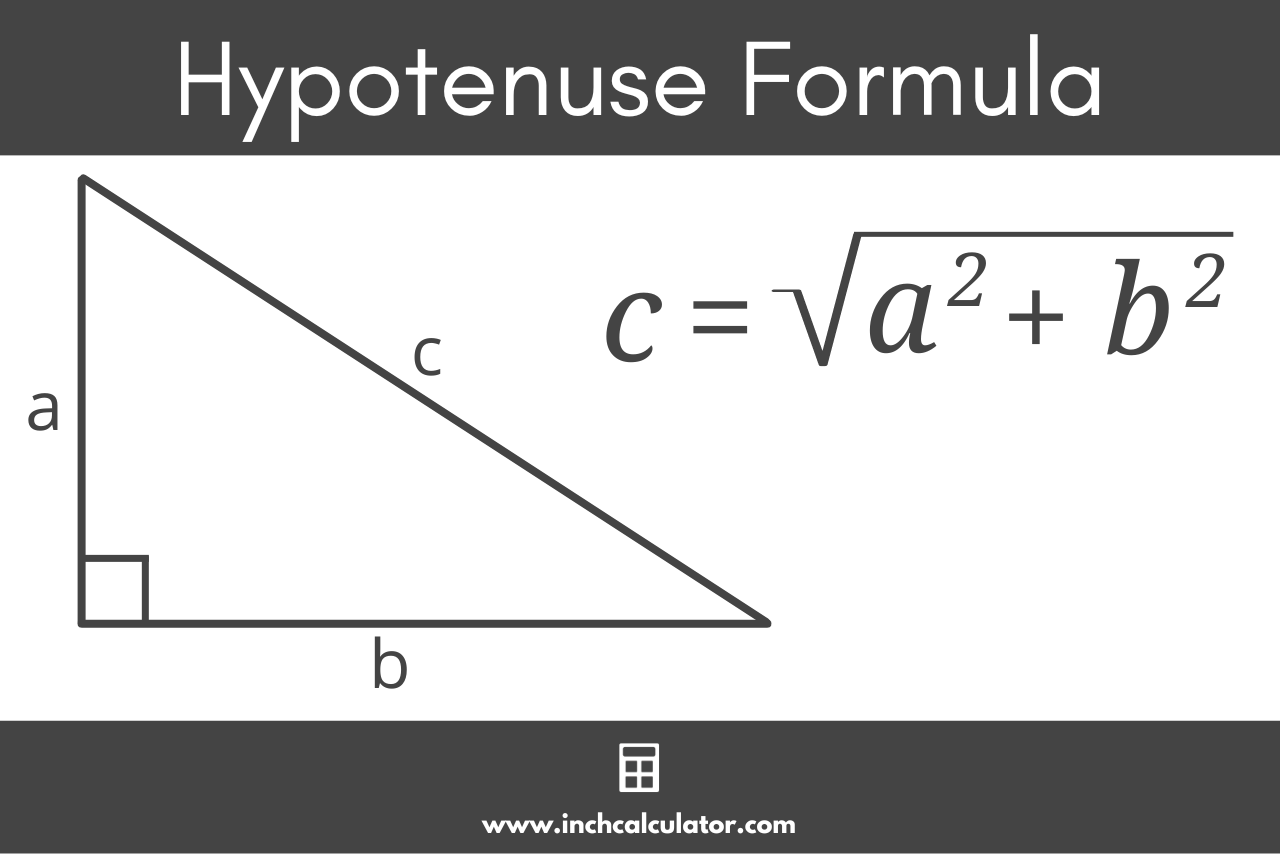
The Pythagorean theorem can be used to find the hypotenuse using the length of the two legs. The Pythagorean theorem states a² + b² = c².
This formula can be rewritten to solve for the hypotenuse c:
c = a² + b²
Thus, the hypotenuse c is equal to the square root of the quantity leg a squared plus leg b squared.
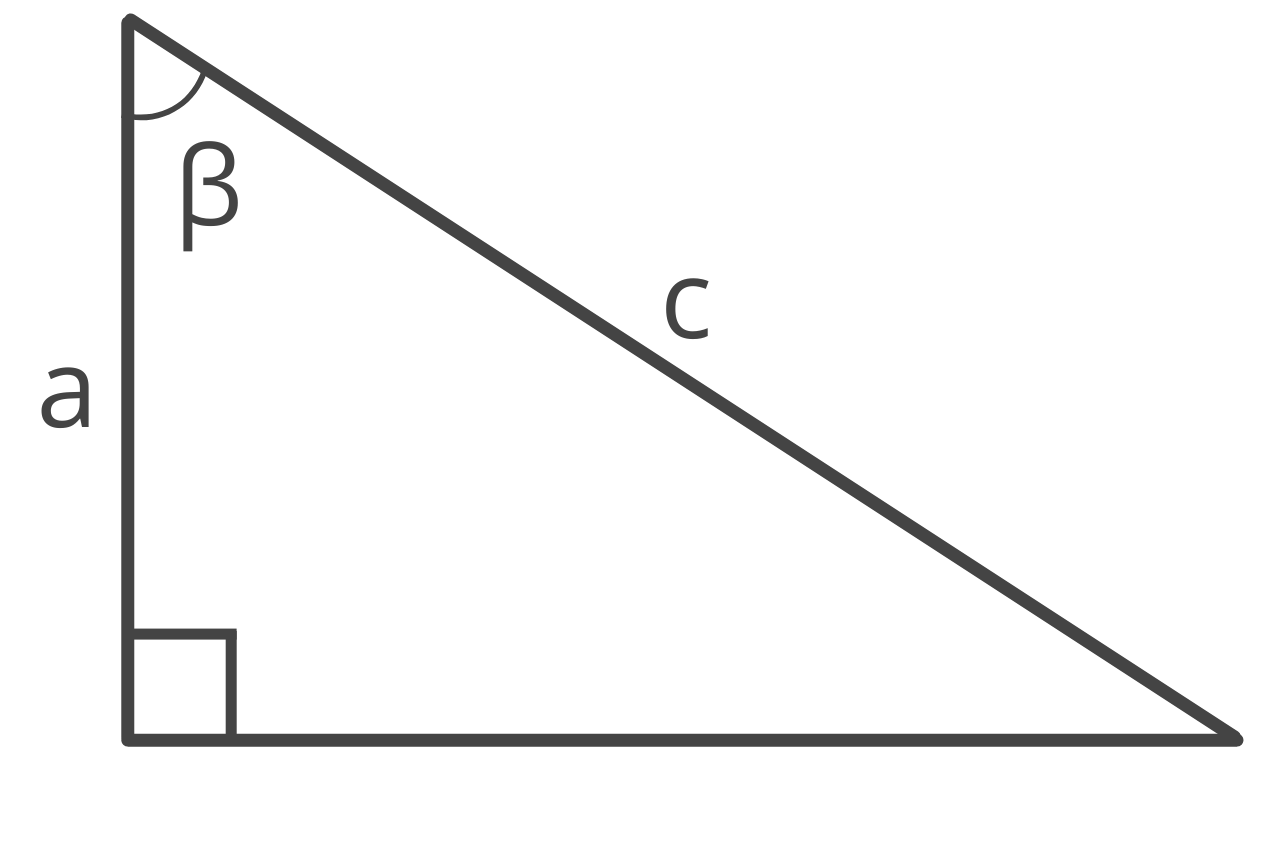
Formula Two: Given One Leg and the Adjacent Angle
Given the length of one leg and the adjacent angle, you can find the hypotenuse using the formula:
c = a / cos(β)
The hypotenuse c is equal to side a divided by the cosine of the adjacent angle β.
Formula Three: Given One Leg and the Opposite Angle
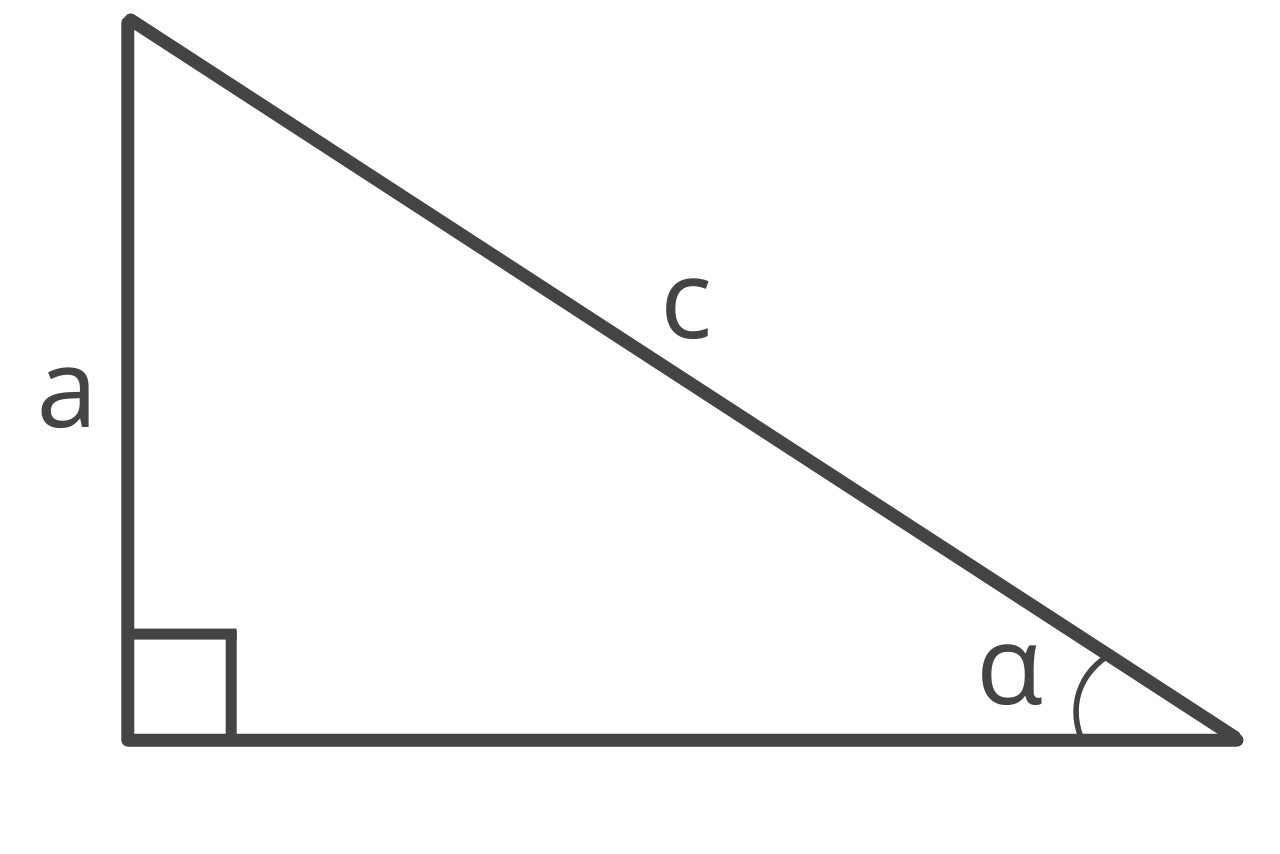
Given the length of one leg and the opposite angle, you can find the hypotenuse using the Law of Sines with the formula:
c = a / sin(α)
The hypotenuse c is equal to side a divided by the sine of the opposite angle α.
Formula Four: Given One Leg and the Area
If you know the length of one of the legs and the triangle area, you can find the length of the hypotenuse by using the area formula to solve for the length of the other leg, then using the Pythagorean theorem.
Given the formula to find the area of a right triangle, start by finding the length of the other leg:
A = 1 / 2ab
You can rearrange this formula to solve for the length of leg b like this:
b = 2A / a
The length of leg b is equal to 2 times the area A divided by the length of leg a.
Then, you can use the length of legs a and b to find the hypotenuse using the first formula above:
c = a² + b²
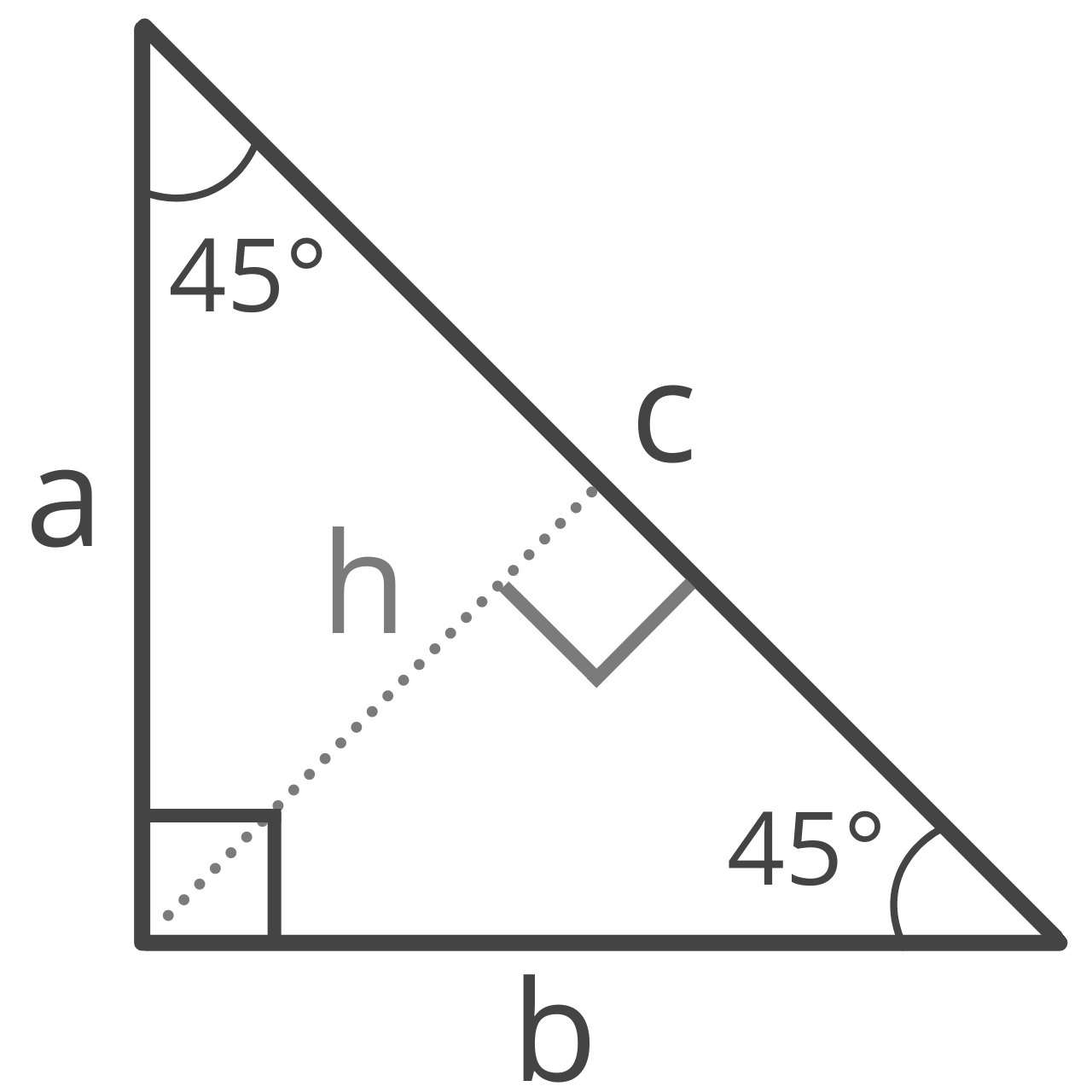
How to Find the Hypotenuse for a 45 45 90 Right Triangle
A 45 45 90 triangle is a special right triangle that is also an isosceles triangle. As the name implies, a 45 45 90 has two 45° interior angles and one right interior angle.
Since this is an isosceles triangle, both legs are equal in length, so you can find the length of the hypotenuse of a 45 45 90 right triangle using a simplified formula derived from the Pythagorean theorem.
c = a√2
The length of hypotenuse c is equal to the length of leg a times the square root of 2.
How to Find the Hypotenuse for a 30 60 90 Right Triangle
A 30 60 90 triangle is a special right triangle that has one 30° interior angle, one 60° interior angle, and one right interior angle.
In this special case, the length of the hypotenuse is always equal to two times the length of the shortest leg a of the triangle. Note, the shortest leg will always be opposite the 30° interior angle.
So, given the length of the shortest leg a, the formula to find the hypotenuse is:
c = 2a
The length of hypotenuse c is equal to 2 times the length of leg a.
