Right Triangle Calculator
Enter any two known values for a right triangle below to calculate the edge lengths, altitude, angles, area, perimeter, inradius, and circumradius.
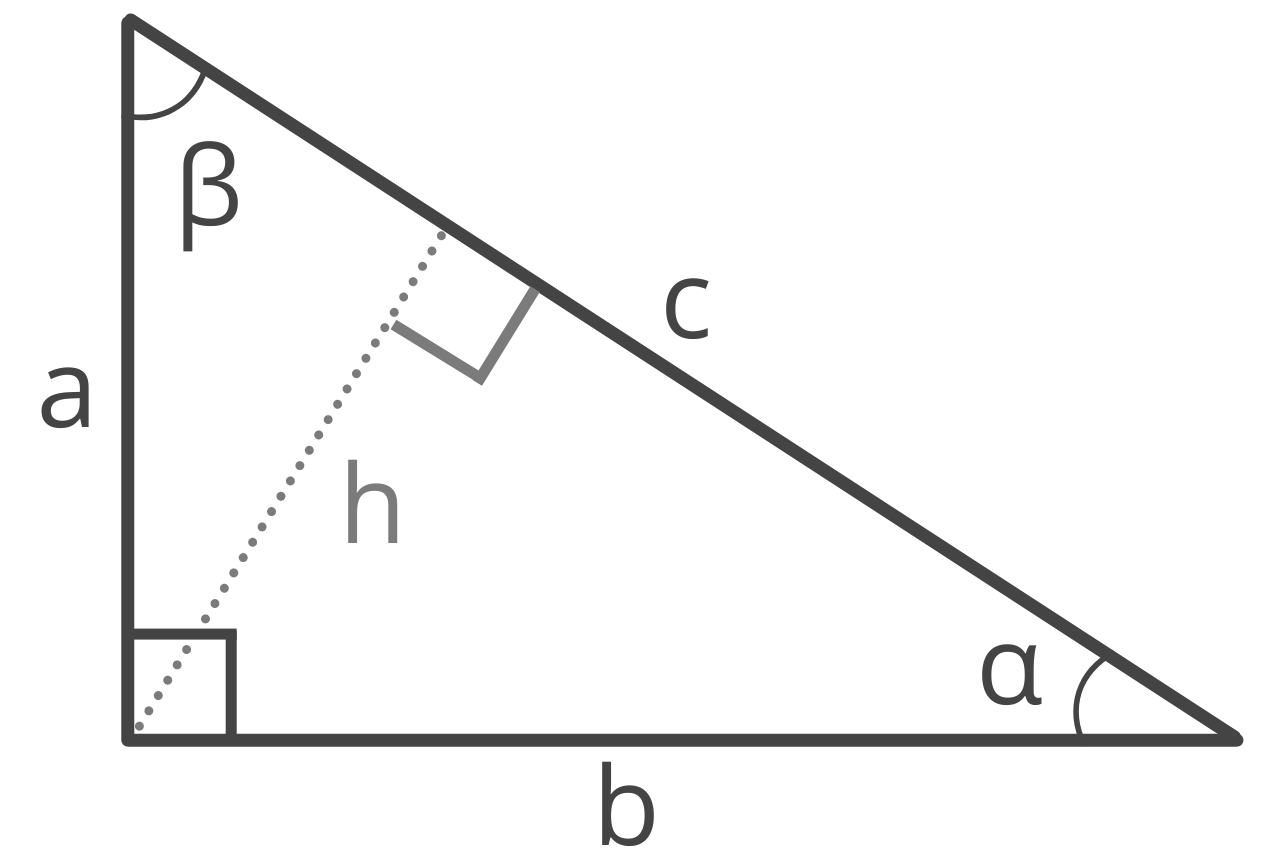
Right Triangle Properties:
| leg a: | 3
|
| leg b: | 4
|
| hypotenuse c: | 5
|
| angle α: | |
| angle β: | |
| height h: | 2.4
|
| area: | 6
|
| perimeter: | 12
|
| inradius: | 1
|
| circumradius: | 2.5
|
Type of Right Triangle:
(3:4:5 Pythagorean triple)
On this page:
- Calculator
- What is a Right Triangle?
- Types of Right Triangles
- How to Find the Hypotenuse of a Right Triangle
- How to Find a Missing Side
- How to Find the Angle of a Right Triangle
- How to Find the Area of a Right Triangle
- Method One: Using Two Legs
- Method Two: Using Hypotenuse and One Leg
- Method Three: Using One Leg and One Angle
- How to Find the Perimeter
- Special Right Triangles
- Formulas for 30 60 90 Right Triangles
- Formulas for 45 45 90 Right Triangles
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
Zach is a former math teacher with a Master's degree in education and a Bachelor's degree in mathematics, and is currently pursuing his PhD.
What is a Right Triangle?
A right triangle, sometimes called a right-angled triangle, is a triangle that has one interior angle equal to exactly 90 degrees, forming what is called a right angle.
The sides adjacent to the right angle are referred to as legs a and b, and are also often referred to as the base and height. The calculator uses the term height to represent the altitude of a triangle.
The side opposite the right angle is called the hypotenuse c.
Types of Right Triangles
Right triangles can be broken into two categories: isosceles and scalene.
An isosceles right triangle is a special isosceles triangle that has two angles that are 45 degrees and legs a and b of equal length.
A scalene right triangle is one where all the angles are unequal, and all the sides are unequal in length.
How to Find the Hypotenuse of a Right Triangle
To calculate the length of the hypotenuse in a right triangle when you know the length of the two legs, you can use the Pythagorean theorem.
The Pythagorean theorem states that side a squared plus side b squared is equal to side c squared. Note, keep in mind that sides a and b specifically refer to the legs, and side c refers to the hypotenuse.
a² + b² = c²
To find the hypotenuse, take the square root of the sum of a squared and b squared.
c = a² + b²
So, the value of the hypotenuse is equal to the square root of leg a squared plus leg b squared.
For example, let’s find the hypotenuse c for a triangle with leg a = 3 and leg b = 4.
3² + 4² = c²
9 + 16 = c²
25 = c²
25 = c
5 = c
So, the hypotenuse c is equal to 5 for a right triangle with legs a = 3 and b = 4.
How to Find a Missing Side
To calculate the length of a missing side, you can use a known side and the hypotenuse and rearrange the Pythagorean theorem to solve the missing variable.
For instance, to find leg b, rearrange the Pythagorean theorem to solve for b by subtracting a² from both sides.
a² + b² = c²
a² + b² – a² = c² – a²
b² = c² – a²
Then take the square root of the right side of the equation to isolate the missing leg, which is b in this example.
b = c² – a²
So, the value of the missing leg b is equal to the square root of the hypotenuse c squared minus the length of the known leg a squared.
How to Find the Angle of a Right Triangle
If you know the lengths of two sides of a right triangle, then you can determine the interior angles using the trigonometric functions sine, cosine, and tangent. These are usually shortened to sin, cos, and tan.
To find the angle given two side lengths, you can use the following formulas:
sin(θ) = opposite ÷ hypotenuse
cos(θ) = adjacent ÷ hypotenuse
tan(θ) = opposite ÷ adjacent
In a right triangle, the adjacent side to θ is the side of the triangle that forms part of the angle θ but is not the hypotenuse. The opposite side to θ is the side that does not form part of the angle θ.
To find one of the angles, choose the formula that can be used given the two known side lengths, then substitute the known values in the formula and solve.
For example, let’s find the angle of a triangle if the adjacent side length is 7 and the hypotenuse is 15.
Start by choosing the equation using adjacent and hypotenuse:
cos(θ) = adjacent ÷ hypotenuse
cos(θ) = 7 ÷ 15
cos(θ) = 0.4667
θ = cos-1(0.4667)
θ = 62.18°
So, for a right triangle with angle θ, with an adjacent side length of 7 and hypotenuse of 15, the angle θ is 62.18°. Note, in the above example, the inverse of cosine was used in the second to last question to isolate θ.
You can find the remaining angle in a few ways. The first way is to repeat using the same method as before, but with a different formula to find the remaining angle.
You can also use the special rule of triangles where the sum of all angles must equal 180°. Subtract 90° (because this is a right triangle, we know one of the angles is 90°) and the angle you just found from 180 to find the missing angle.
You can use the mnemonic SOHCAHTOA to help remember the equations above.
If you split SOHCAHTOA into three parts, each part represents one of the formulas, where each letter is the first letter in the part of the equation.
SOH · CAH · TOA
SOH: sin(θ) = opposite ÷ hypotenuse
CAH: cos(θ) = adjacent ÷ hypotenuse
TOA: tan(θ) = opposite ÷ adjacent
Learn more about using this mnemonic on our SOHCAHTOA calculator.
How to Find the Area of a Right Triangle
There are a few methods to find the area of a right triangle.
Method One: Using Two Legs
If you know the length of the two legs in a right triangle, then you can find the area using the formula:
A = 1 / 2a × b
The area A of a right triangle is equal to one-half times leg a times leg b.
Method Two: Using Hypotenuse and One Leg
If you know the hypotenuse and one of the legs, then you can use a variation of the Pythagorean theorem to find the area:
A = a × 1 / 2c² – a²
The area A of a right triangle is equal to leg a times 1/2 times the square root of the hypotenuse c squared times minus leg a squared. Notice the √(c² – a²) portion of this formula is simply the Pythagorean theorem isolated for b.
Method Three: Using One Leg and One Angle
If you know the length of one leg and the value of an adjacent angle, then you can use the tangent function to find the area.
Given the value of leg a and angle β, find the area using the following formula:
A = a² × tan(β) / 2
Given the value of leg b and angle α, find the area using the following formula:
A = b² × tan(α) / 2
The area A of a right triangle is equal to leg a squared times one-half the tangent of angle β, or leg b squared times one-half the tangent of angle α.
Keep in mind that in the above formulas, angle β must be adjacent to leg a, and angle α must be adjacent to leg b.
How to Find the Perimeter
The formula to find the perimeter of a right triangle is:
perimeter = a + b + c
The perimeter is equal to leg a plus leg b plus hypotenuse c.
You can use the formulas above to find the lengths of the missing leg or hypotenuse if any are missing.
Special Right Triangles
There are a few types of special right triangles, which are triangles that have specific proportions. These special right triangles also have formulas to simplify solving them.
Formulas for 30 60 90 Right Triangles
A 30 60 90 triangle is a special right triangle with 30° and 60° interior angles adjacent to the right 90° angle.
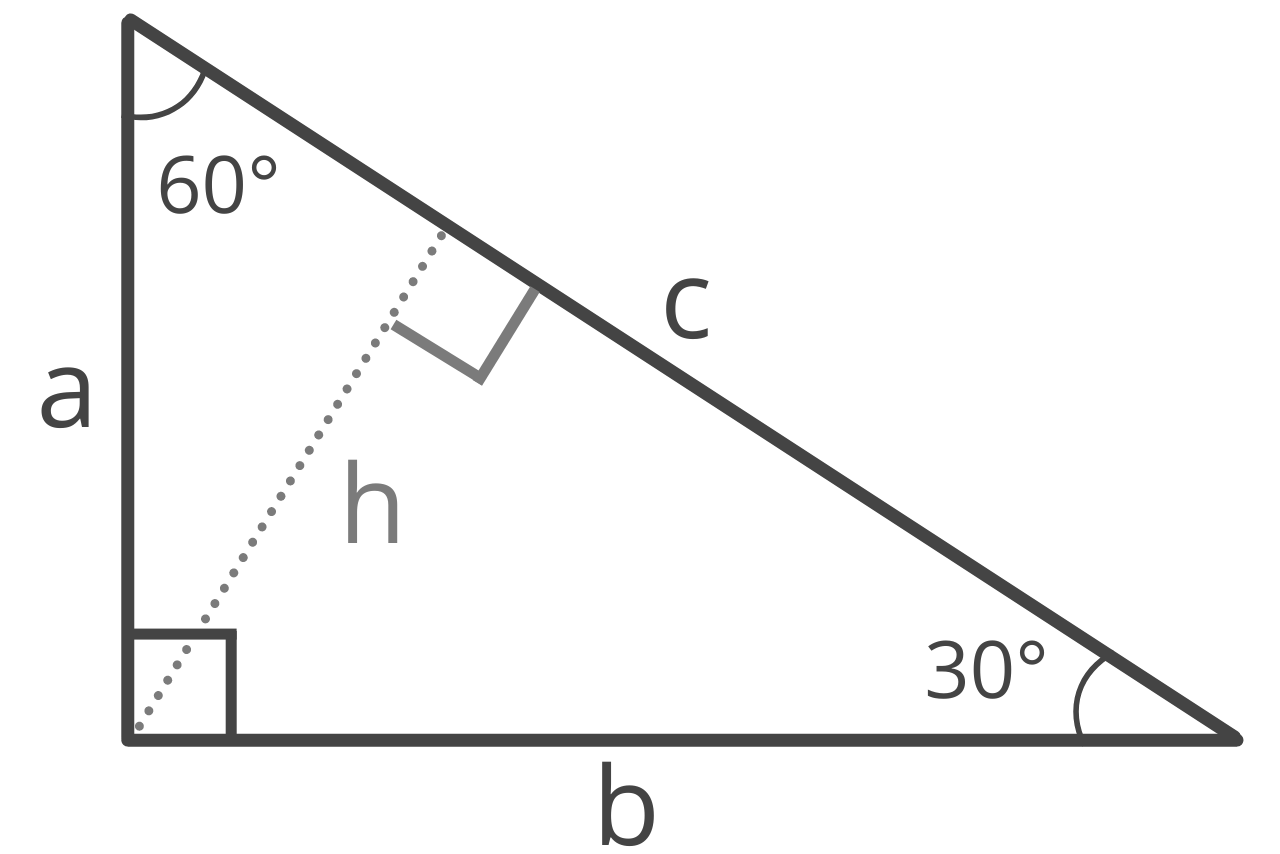
Leg a
Given the length of leg b (the side opposite the 60° angle), the formula to find the length of a is:
a = b × √3 / 3
The length of leg a is equal to b times the square root of 3, divided by 3.
Leg b
Given the length of leg a (the side opposite the 30° angle), the formula to find the length of b is:
b = a√3
The length of leg b is equal to a times the square root of 3.
Hypotenuse c
In the case of a 30 60 90 right triangle, the length of the hypotenuse is always equal to two times the length of the shortest leg. So, given the length of the short leg a, the formula to find the hypotenuse is:
c = 2a
The length of c is equal to 2 times a.
Formulas for 45 45 90 Right Triangles
A 45 45 90 triangle is a special right isosceles triangle with 45° interior angles adjacent to the 90° right angle.
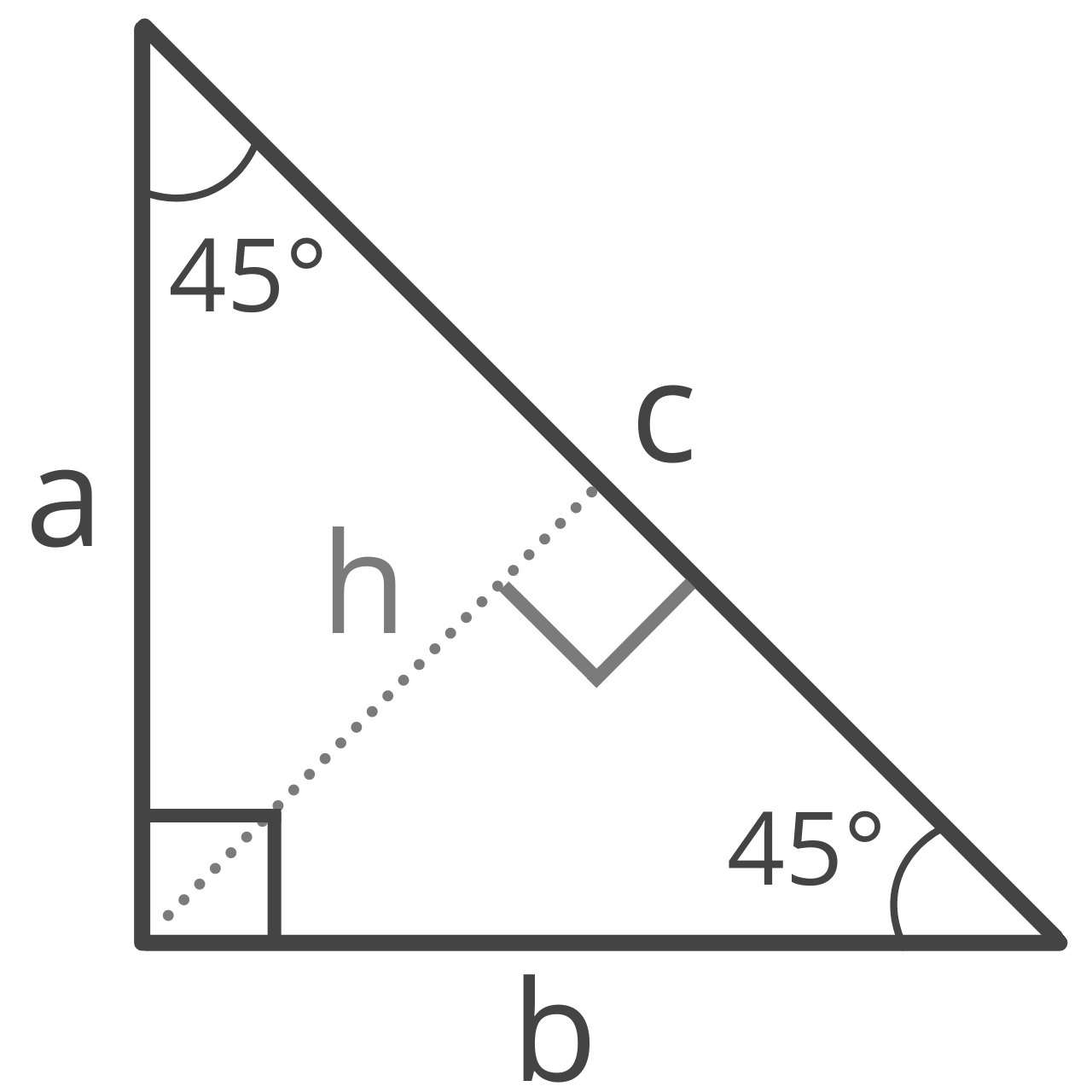
Legs a & b
Given the hypotenuse, you can find the length of the legs a and b in a 45 45 90 triangle using the formula:
a = b = c√2 / 2
The length of legs a and b are equal to hypotenuse c times the square root of 2, divided by 2.
Hypotenuse c
Since it is an isosceles triangle, both legs are the same length, so there is a special formula to find the length of the hypotenuse.
c = a√2
The length of side c is equal to the length of side a times the square root of 2.
Area
There is also a special formula to find the area of a 45 45 90 right triangle:
A = a² / 2
The area A of the right triangle is equal to the length of leg a squared, divided by 2.