Isosceles Triangle Calculator
Enter any two known values for an isosceles triangle to calculate the edge lengths, altitude, angles, area, perimeter, inradius, and circumradius.
Solution:
| side a: | 3
|
| base b: | 5
|
| angle α: | 33.557° | 0.5857 rad
|
| angle β: | 112.89° | 1.97 rad
|
| height h: | 1.658
|
| area: | 4.146
|
| perimeter: | 11
|
| inradius: | 0.7538
|
| circumradius: | 2.714
|
Type of Triangle:
On this page:
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
Zach is a former math teacher with a Master's degree in education and a Bachelor's degree in mathematics, and is currently pursuing his PhD.
What is an Isosceles Triangle?
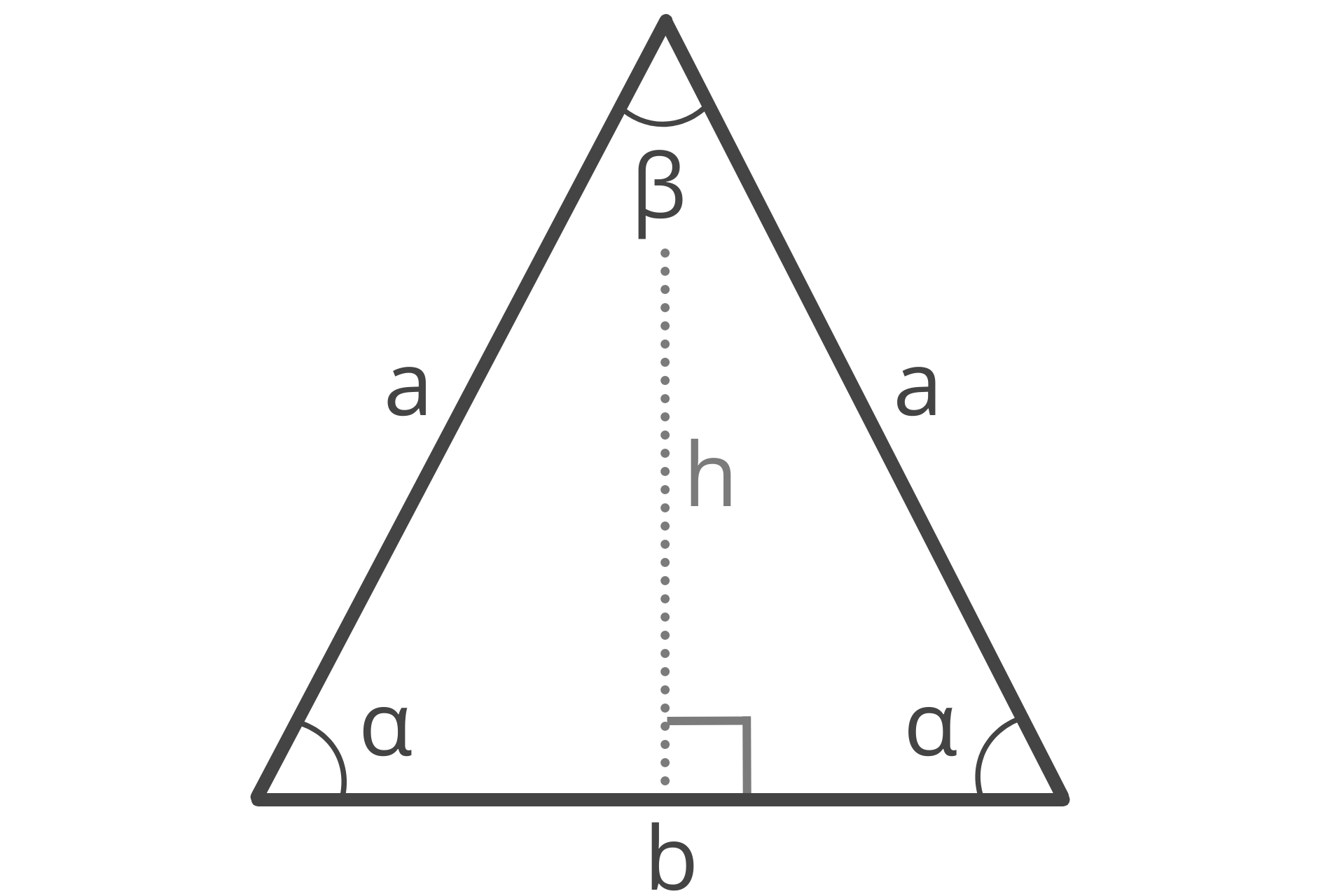
An isosceles triangle is a triangle that has two sides of equal length. The third side is often referred to as the base. Isosceles triangles are typically considered to have exactly two sides of equal length.
However, sometimes they are referred to as having at least two sides of equal length. The equilateral triangle, for example, is considered a special case of the isosceles triangle.
The two interior angles adjacent to the base are called the base angles, while the interior angle opposite the base is called the vertex angle. When references are made to the angles of a triangle, they are most commonly referring to the interior angles.
Because the side lengths opposite the base angles are of equal length, the base angles are also identical. Note, this means that any reference made to side length a applies to either of the identical side lengths as they are equal, and any reference made to base angle α applies to either of the base angles as they are also identical.
Types of Isosceles Triangles
There are four types of isosceles triangles: acute, obtuse, equilateral, and right.
An acute isosceles triangle is an isosceles triangle with a vertex angle less than 90°, but not equal to 60°.
An obtuse isosceles triangle is an isosceles triangle with a vertex angle greater than 90°.
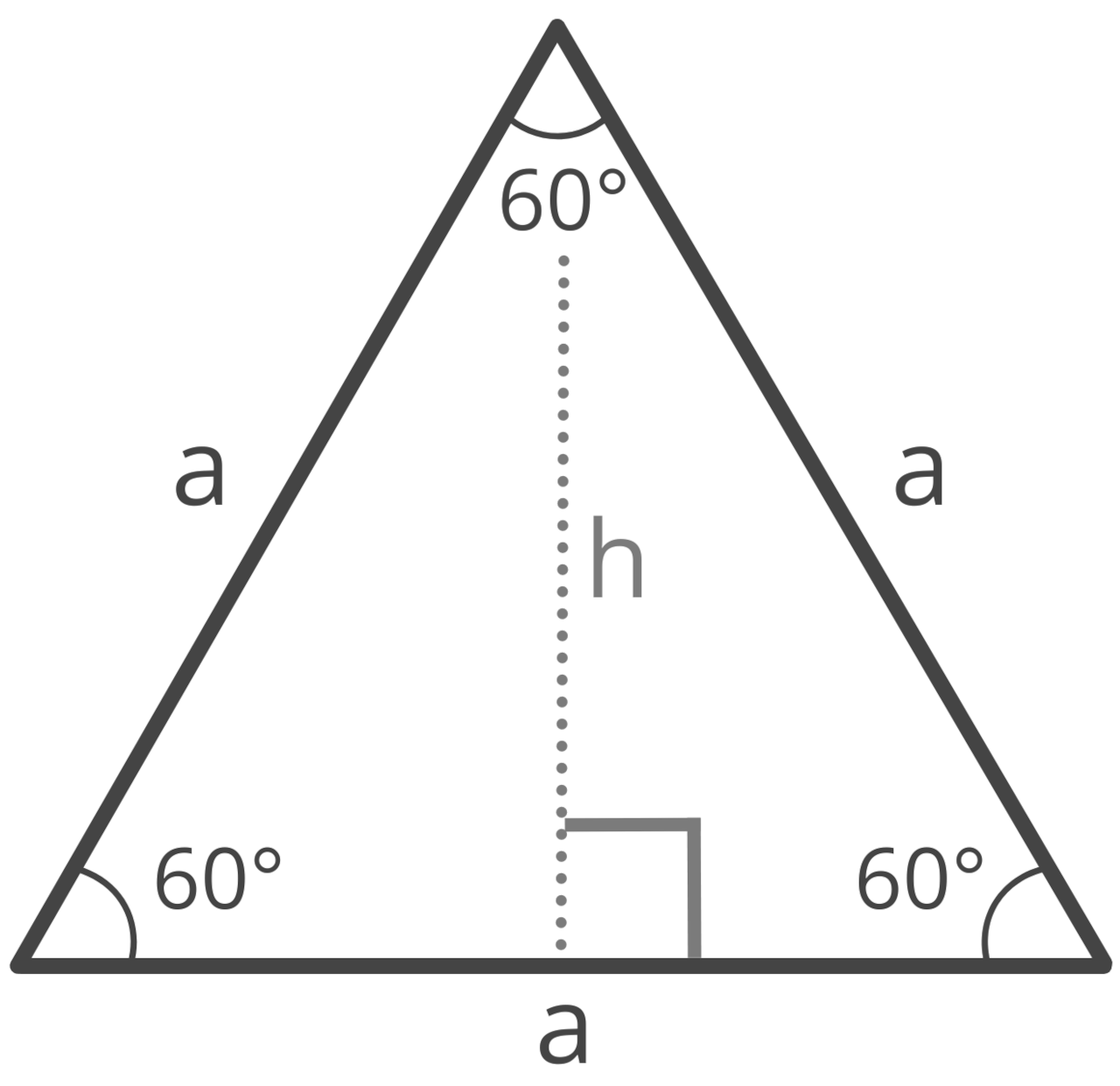
An equilateral triangle is a special case of isosceles triangles. Note, in an equilateral triangle, all three interior angles are identical to one another, and all three side lengths are equal to one another.
Thus, the vertex angle of an equilateral triangle is equal to 60°, as are the base angles. Try our equilateral triangle calculator.
A right isosceles triangle is an isosceles triangle with a vertex angle equal to 90°, and base angles equal to 45°. This is also referred to as a 45 45 90 special right triangle.
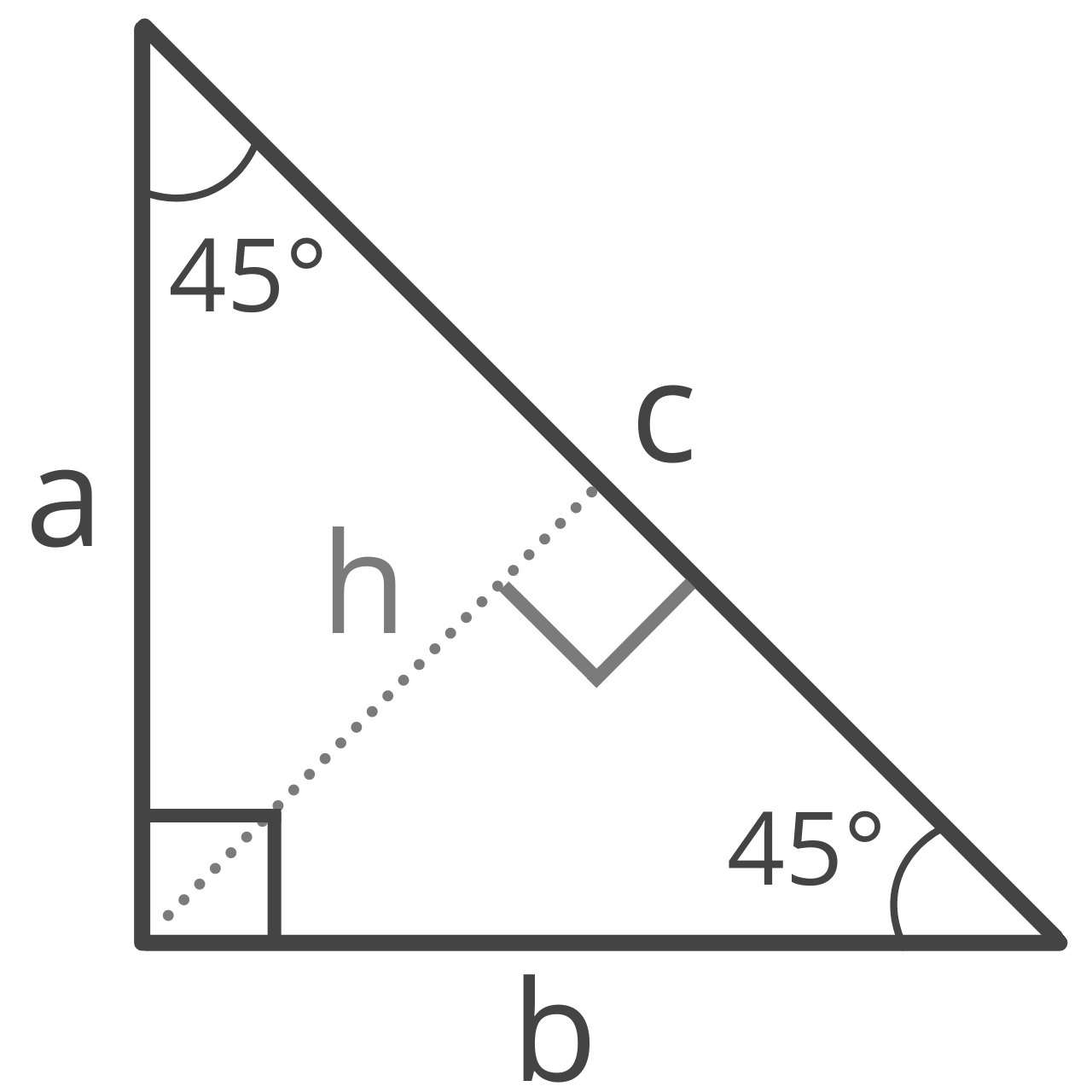
We have a special right triangle calculator to calculate this type of triangle.
How to Calculate Edge Lengths of an Isosceles Triangle
Given the height, or altitude, of an isosceles triangle and the length of one of the sides or the base, it’s possible to calculate the length of the other sides.
Find the Base Length
Use the following formula derived from the Pythagorean theorem to solve the length of the base side:
b = 2a² – h²
The base length b is equal to 2 times the square root of quantity leg a squared minus the height h squared.
Find the Leg Length
Use the following formula also derived from the Pythagorean theorem to solve the length of side a:
a = h² + (b ÷ 2)²
The side length a is equal to the square root of the quantity height h squared plus one-half of base b squared.
How to Calculate the Angles of an Isosceles Triangle
Given any angle in an isosceles triangle, it is possible to solve the other angles.
Find the Base Angle
Use the following formula to solve either of the base angles:
α = 180° – β / 2
The base angle α is equal to quantity 180° minus vertex angle β, divided by 2.
Find the Vertex Angle
Use the following formula to solve the vertex angle:
β = 180° – 2α
The vertex angle β is equal to 180° minus 2 times the base angle α.
How to Calculate Area and Perimeter
Given the side lengths of an isosceles triangle, it is possible to solve the perimeter and area using a few simple formulas.
Find the Perimeter
You can find the perimeter of an isosceles triangle using the following formula:
p = 2a + b
Thus, the perimeter p is equal to 2 times side a plus base b.
Find the Semiperimeter
Given the perimeter, you can find the semiperimeter. The semiperimeter s is equal to half the perimeter.
s = p / 2
Find the Area
You can find the area of an isosceles triangle using the formula:
A = s(s – a)(s – a)(s – b)
The area A is equal to the square root of the semiperimeter s times semiperimeter s minus side a times semiperimeter s minus a times semiperimeter s minus base b.
This is known as Heron’s formula.