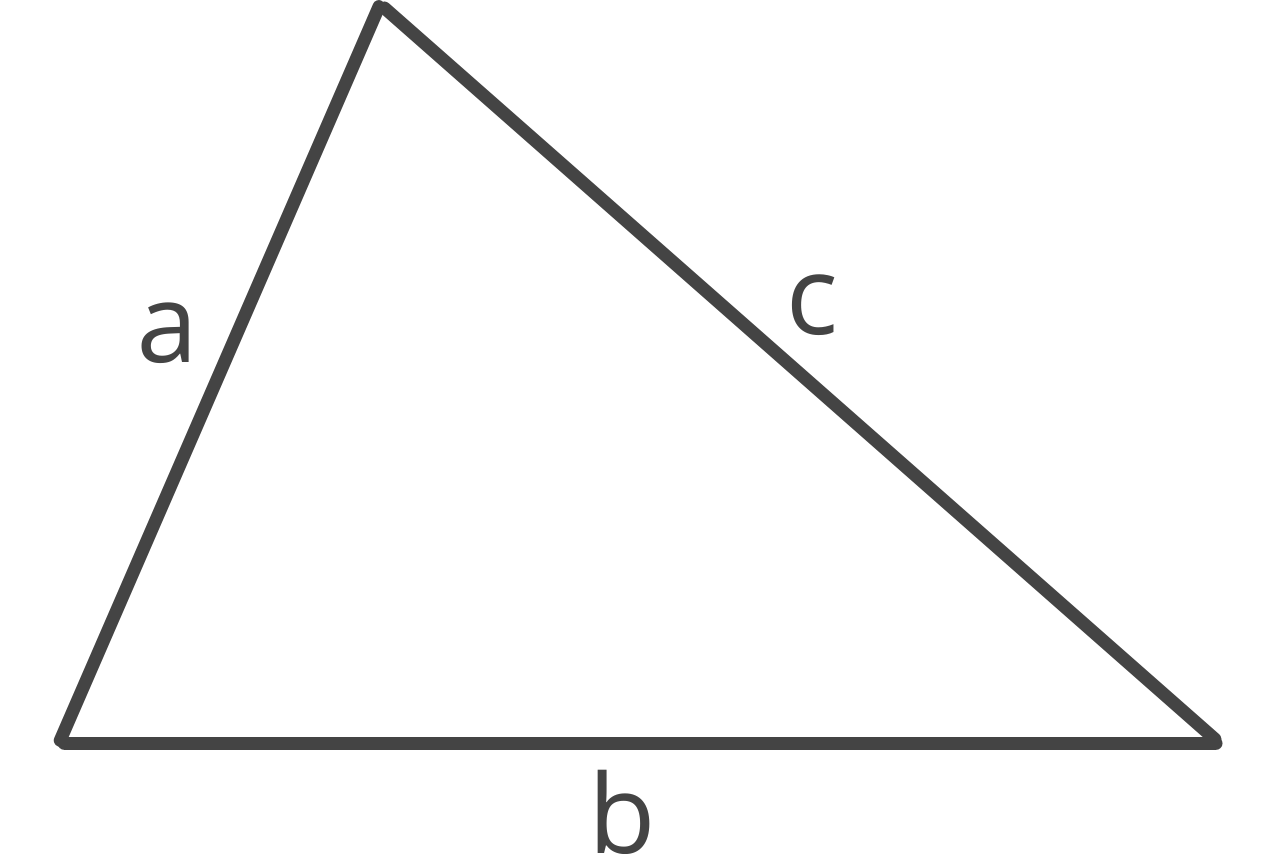
Triangle Perimeter Calculator
Solve the perimeter of a triangle using three sides, two sides & one angle, or one side & two angles with the calculator below.
Solution:
On this page:
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
How to Find the Perimeter of a Triangle
The perimeter of a triangle is the distance, or length, of the boundary around the shape. The perimeter of a triangle is the sum of its sides.
Unlike area, the perimeter is the distance around the shape, not the amount of space the shape consumes.
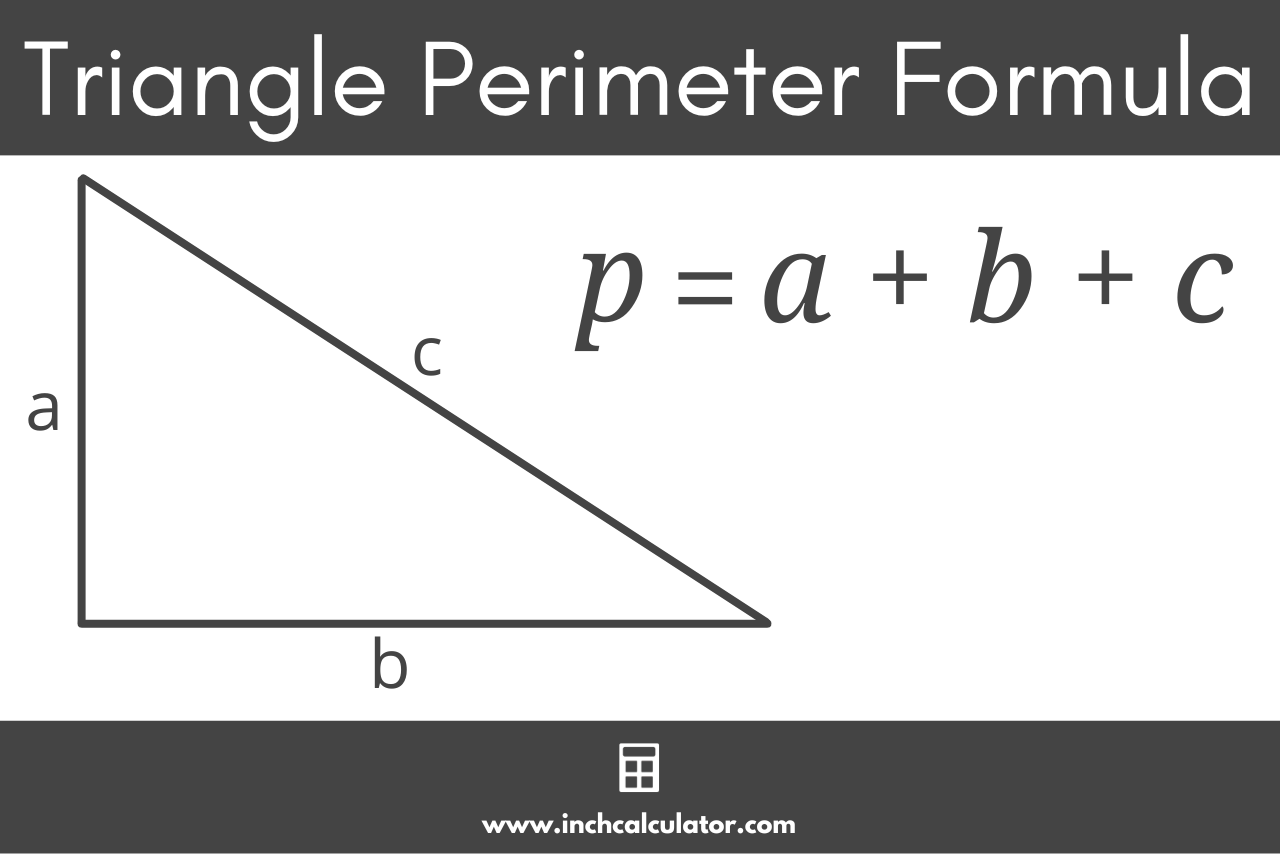
The formula to solve the perimeter of a triangle given all three sides is:
p = a + b + c
Thus, the perimeter p is equal to side a plus side b plus side c. This is referred to as the SSS method.
How to Solve Triangle Perimeter Without Three Sides
Solving the perimeter of a triangle requires knowing the length of all three sides. If the length of the sides is unknown, then it will be necessary to find the length of the sides first.
You can find the length of the sides of a triangle a few different ways, depending on what parts of the triangle are known.
How Solve Perimeter using Two Sides and One Angle
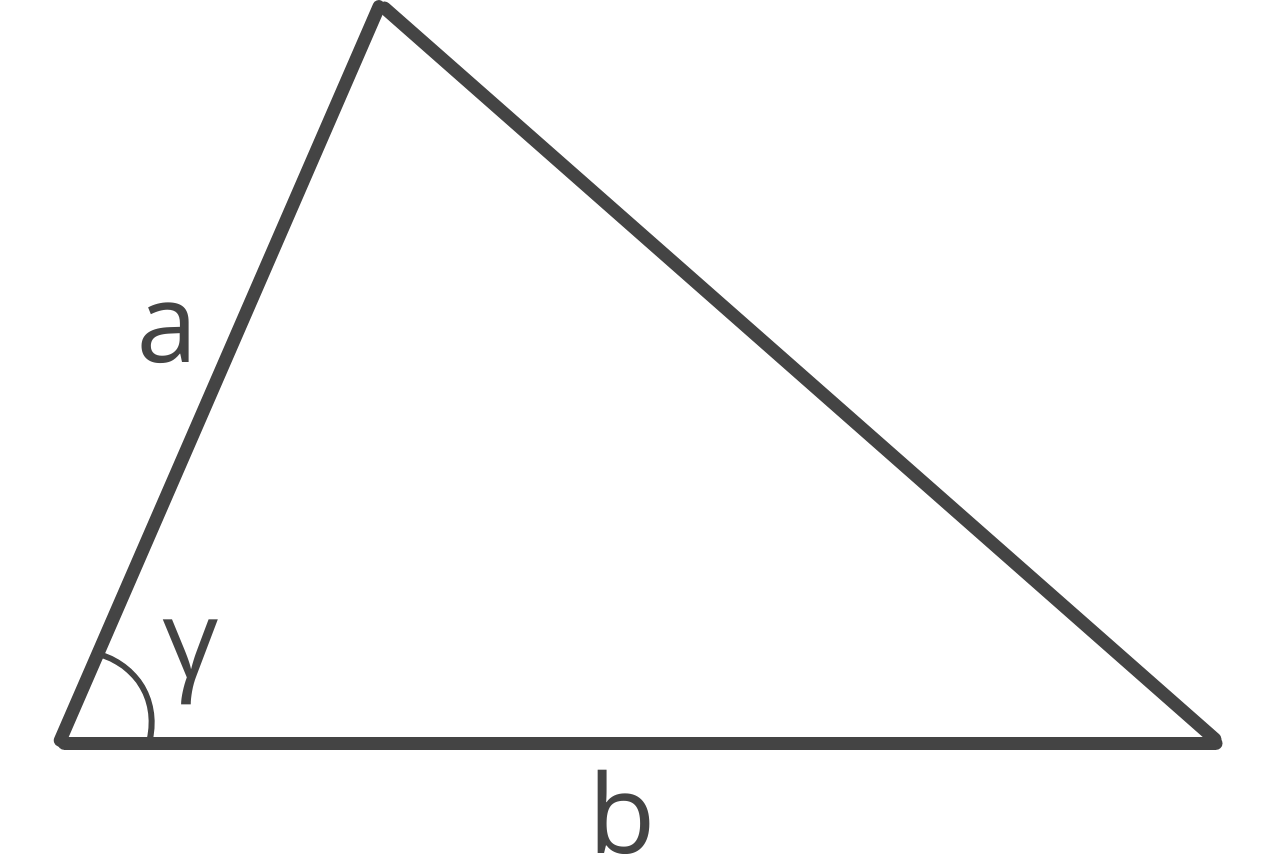
If two sides and the adjacent angle are known, then the perimeter of the triangle can be found using the Law of Cosines with the formula:
p = a + b + (a² + b² – 2 × a × b × cos(γ))
Using the SAS method, the perimeter p is equal to side a plus side b plus the square root of side a squared plus side b squared minus 2 times side a times side b times the cosine of angle γ.
How Solve Perimeter using One Side and Two Angles
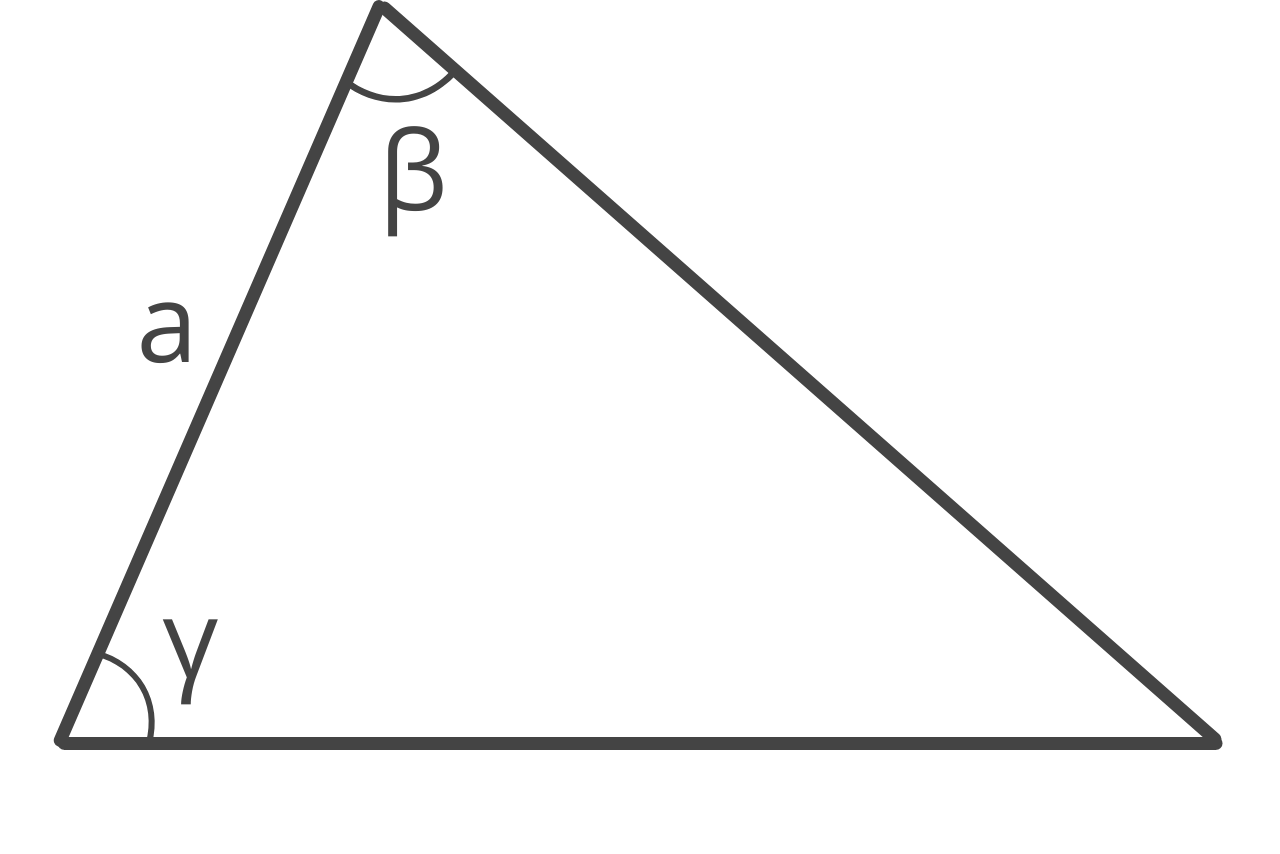
If one side and the two adjacent angles are known, then the perimeter of the triangle can be found using the Law of Sines with the formula:
p = a + (a ÷ sin(β + γ)) × (sin(β) + sin(γ))
Using the ASA method, the perimeter p is equal to side a plus side a divided by the sine of angle β plus angle γ times the sine of angle β plus the sine of angle γ.