Law of Sines Calculator
Use our Law of Sines calculator to find any angle or side of a triangle given other known properties.
Result:
Sides
| a = | 29.5775
|
|---|---|
| b = | 25
|
| c = | 29.5775
|
Angles
| α = | |
|---|---|
| β = | |
| γ = |
Steps to Solve
a / sin(α) = b / sin(β)
a = b · sin(α) / sin(β)
a = 25 · sin(65°) / sin(50°)
a = 29.5775
On this page:
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
Dr. Connor Smith is a professor of electrical and computer engineering with expertise in electromagnetics, microsystems, and magnetic materials and devices.
How to Solve Parts of a Triangle Using the Law of Sines
The Law of Sines, also called the Sine Rule, allows you to determine unknown angles or side lengths in non-right triangles by utilizing the relationships between their sides and angles. The Law of Sines states that in any oblique (scalene) triangle, the ratio of a side length to the sine of its opposite angle is constant.
This relationship can be expressed as follows:[1]
a / sin(α) = b / sin(β) = c / sin(γ)
Where:
a, b, and c are the lengths of the triangle’s sides
α, β, and γ are the angles opposite to sides a, b, and c.
There are special formulas to solve for the sides and angles of a right triangle, but for other triangles, the Law of Sines can be used to solve them.
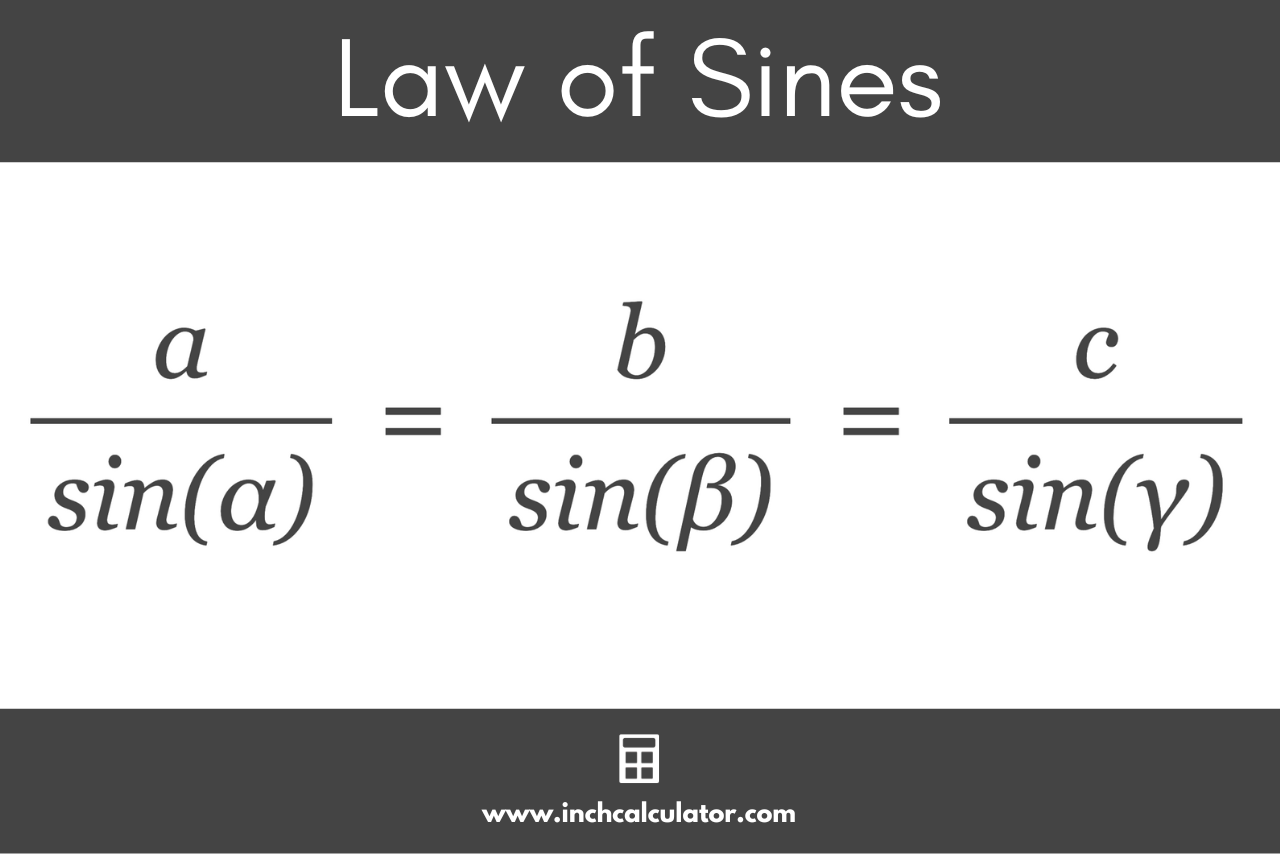
If you know other properties of the triangle, you can solve the remaining sides and angles using the Law of Cosines.
How to Use the Law of Sines
The Law of Sines is particularly useful when you know either:
Two angles and one side (aka AAS): If you know two angles and the length of the side between them or opposite one of those angles.
Two sides and one angle (aka SSA): If you know the lengths of two sides and the value of the angle opposite one of those sides.
To use the Law of Sines, fill in the parts of the equation that you know about the triangle, then rearrange the equation and solve for the remaining portion of the ratio.
It’s important to note that when using the Law of Sines, you may encounter multiple solutions or no solution at all due to its ambiguous nature.
For example, let’s find the missing angle β for a triangle with sides a = 8 and b = 10, and angle α = 40°.
Start by substituting the known values into the Law of Sines.
8 / sin(40°) = 10 / sin(β)
Rearrange the equation and solve.
sin(β) = 10 · sin(40°) / 8
You’ll need to use the inverse sine to solve the remaining equation.
β = sin-1[10 · sin(40°) / 8]
β = 53.46°
Frequently Asked Questions
Does the Law of Sines apply to right triangles?
Yes! You can use the Law of Sines ratios to solve the properties for all types of triangles, including right triangles, equilateral triangles, and isosceles triangles.
When can you use the Law of Sines?
You can use the Law of Sines to solve the properties of a triangle when you know two angles and one side or when you know two sides and an angle opposite to one of them.
How do you identify the sides and angles for the Law of Sines?
When working with triangles, the Law of Sines defines a constant ratio of the sides in the triangle to the angle opposite them. So, given any side, the angle to use in the ratio should be the angle opposite the known side.
References
- Michael Corral, Elementary Trigonometry - 2.1: The Law of Sines, LibreTexts: Mathematics, https://math.libretexts.org/Bookshelves/Precalculus/Elementary_Trigonometry_(Corral)/02%3A_General_Triangles/2.01%3A_The_Law_of_Sines