Equilateral Triangle Calculator
Enter any known value for an equilateral triangle to calculate the edge lengths, altitude, area, perimeter, inradius, and circumradius.
Solution:
| sides a: | 3
|
| height h: | 2.598
|
| area: | 3.897
|
| perimeter: | 9
|
| inradius: | 0.866
|
| circumradius: | 1.732
|
On this page:
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
Zach is a former math teacher with a Master's degree in education and a Bachelor's degree in mathematics, and is currently pursuing his PhD.
What is an Equilateral Triangle?
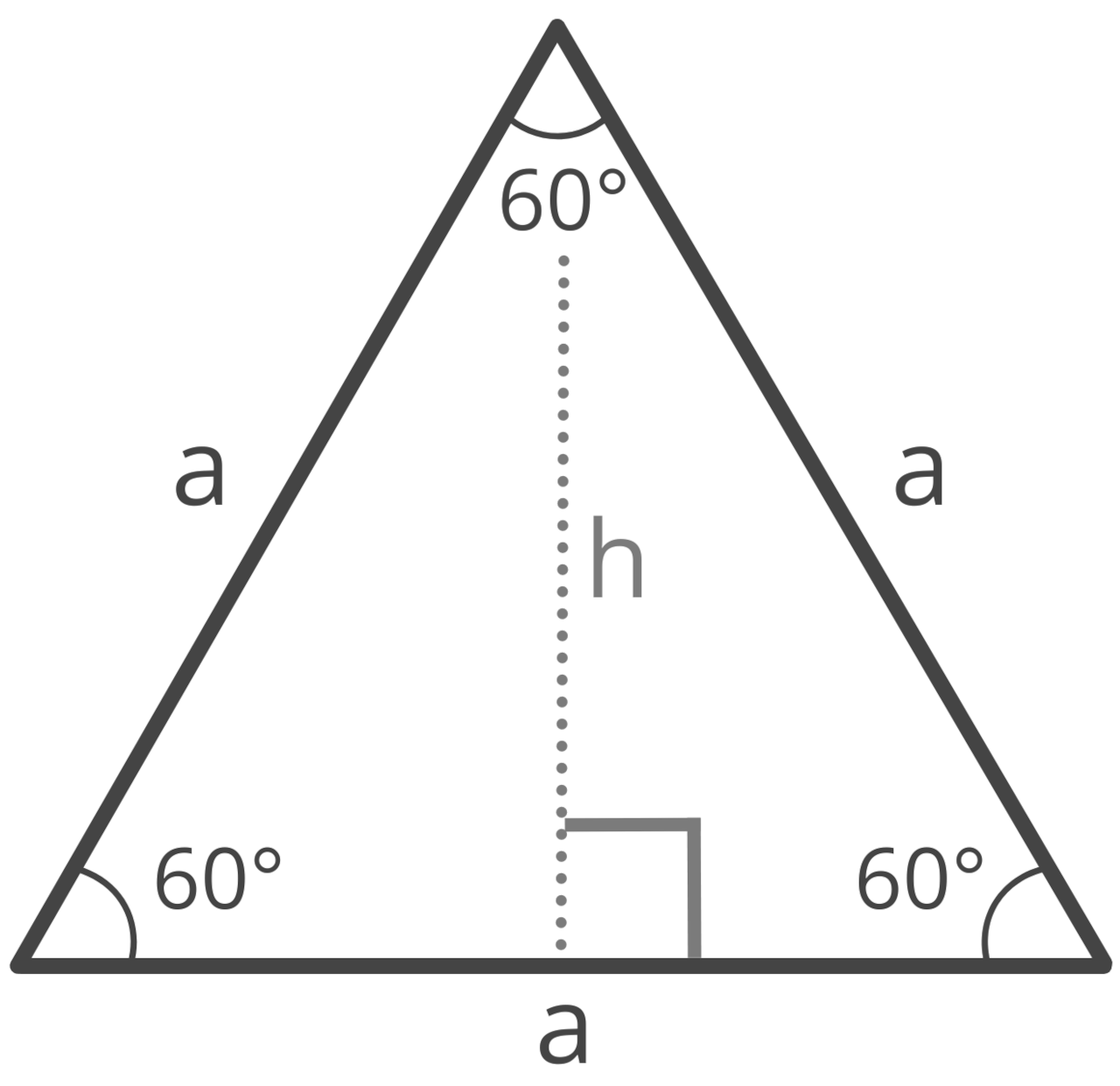
An equilateral triangle, also called a regular triangle, is a triangle with sides of equal length. An equilateral triangle is a special kind of isosceles triangle.
While isosceles triangles are often considered as having exactly two sides of equal length, an equilateral triangle can be labeled as having at least two sides of equal length, since all three side lengths are equal. This is why equilateral triangles are considered a special kind of isosceles triangle.
Since all side lengths are equal, all three interior angles in an equilateral triangle are also equal. Each angle is 60°.
In an equilateral triangle, the height (altitude) is both a median and a perpendicular bisector.
How to Find the Side Lengths of an Equilateral Triangle
You can find the length of an equilateral triangle’s sides if you know the area or perimeter.
Find Sides using Area
Given the area of an equilateral triangle, the side lengths can be found using this formula:
a = (4A) ÷ √3
Thus, the length of side a is equal to the square root of 4 times the area A divided by the square root of 3.
Find Sides using Perimeter
Given the perimeter of an equilateral triangle, the side lengths can be found using this formula:
a = p / 3
Because each side is equal in length, the length of side a is equal to the perimeter p divided by three.
How to Find the Height of an Equilateral Triangle
If you know the side length of an equilateral triangle, you can also solve for the height. Use the formulas above to find the side length, if needed.
h = a * √ 3 / 2
Thus, the height h is equal to the side length a times the square root of 3, divided by 2.
How to Find the Area and Perimeter
Given the side length of an equilateral triangle, the area and perimeter can also be determined.
Area
You can find the area of an equilateral triangle using this formula:
A = √3 / 4a²
The area A of an equilateral triangle is equal to side a squared times the square root of 3, divided by 4.
Perimeter
You can find the perimeter using this formula:
p = 3a
Because each side in an equilateral triangle is equal in length, the perimeter p is equal to 3 times side length a.
How to Find the Inradius and Circumradius
There are also some easy formulas to solve the inradius and circumradius for an equilateral triangle. The center of both the inscribed and circumscribed circle in an equilateral triangle is the point where the angle bisectors and perpendicular bisectors intersect.
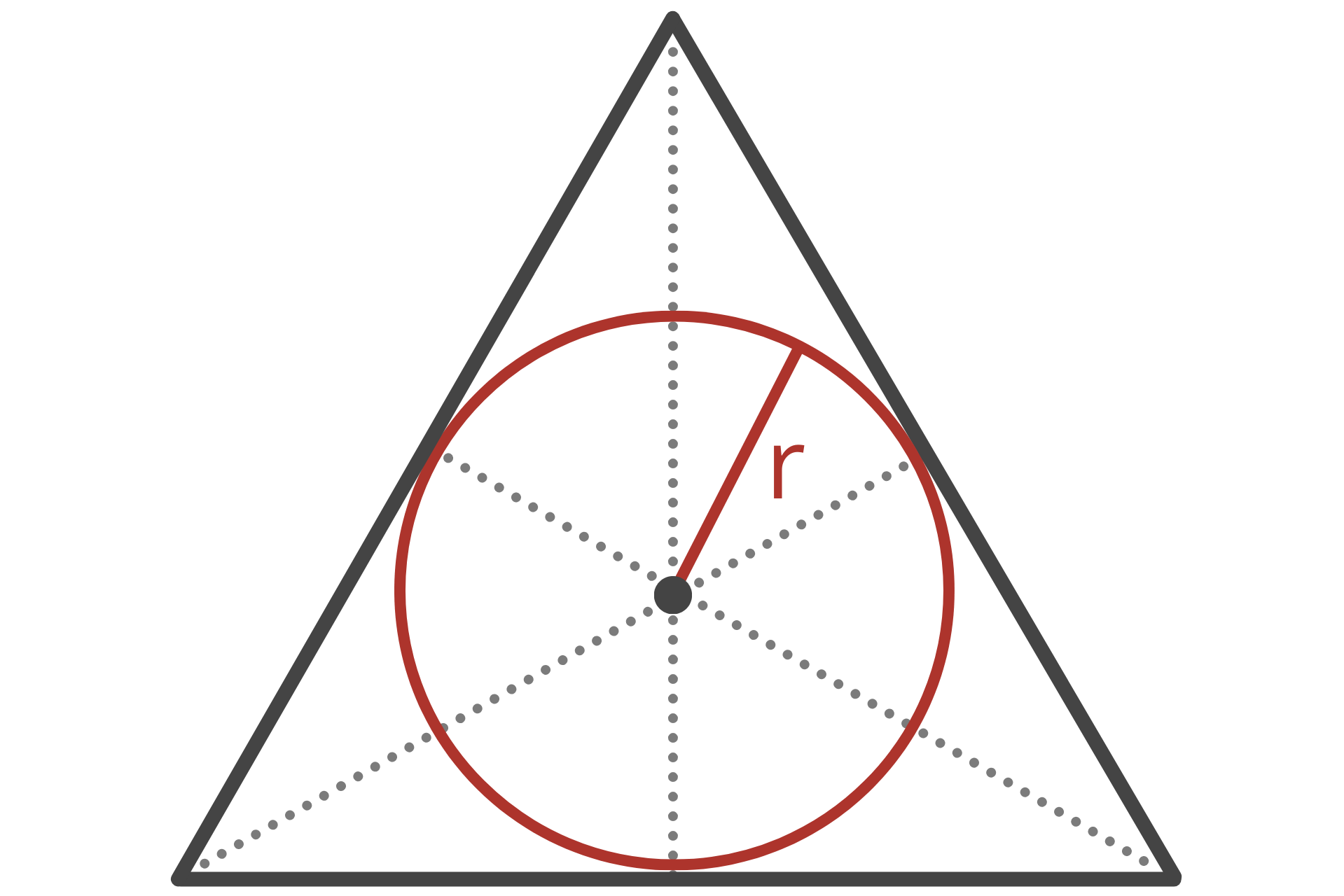
Inradius
The inradius is the radius of the inscribed circle, which is a circle that is tangent to all three sides of the triangle. In other words, it is the largest circle that can fit inside the triangle.
The inradius is equal to 1/2 of the circumradius or 1/3 of the triangle’s height. If the length of a side is known, then the following formula can also be used to determine the inradius.
r = a × √3 / 6
The inradius r of the equilateral triangle is equal to side a times the square root of 3, divided by 6.
Circumradius
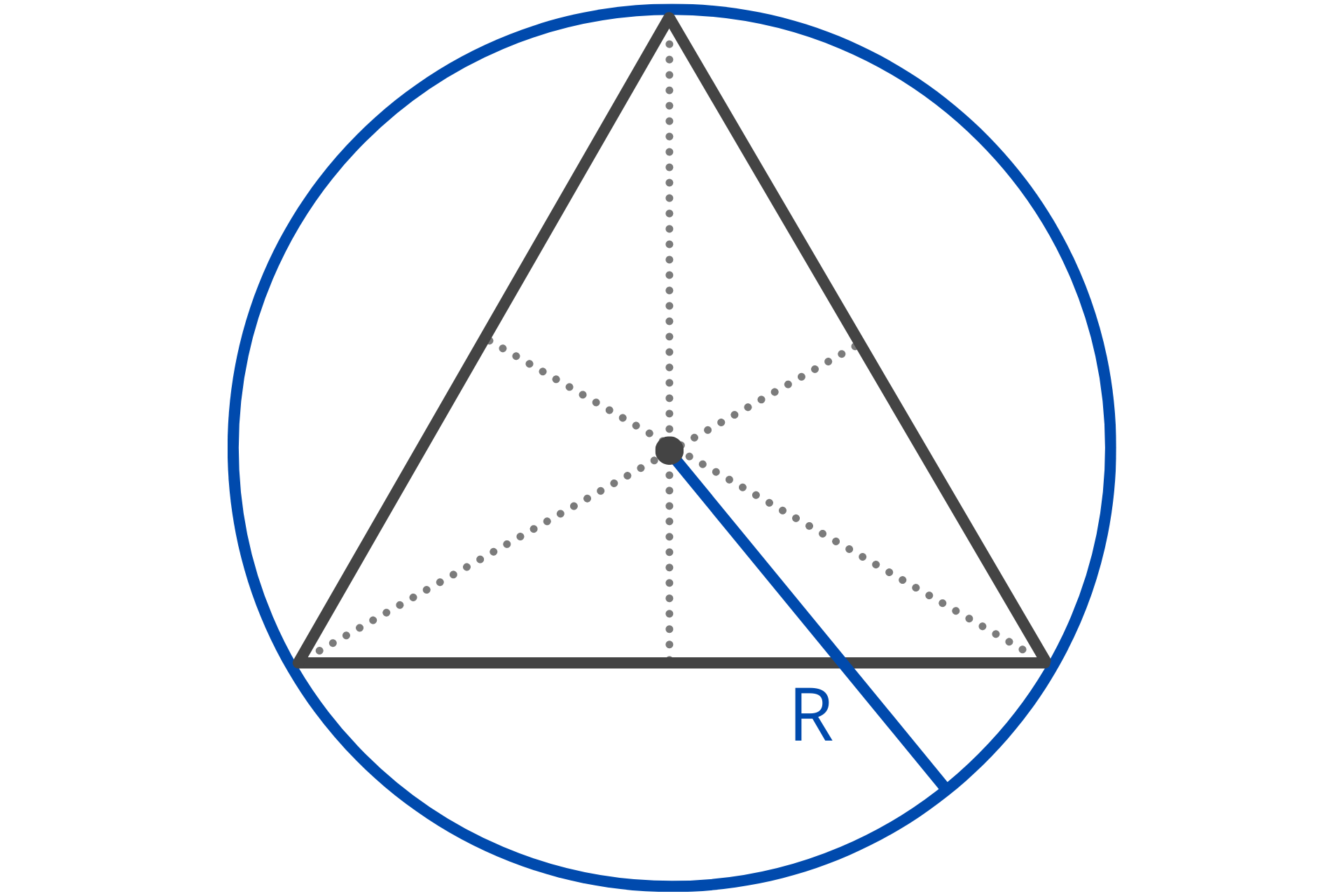
The circumradius is the radius of the circumscribed circle, which is the circle that passes through all three vertices of the triangle.
In other words, it is the smallest circle that the triangle can fit inside of. It’s equal to 2/3 the height, or twice the value of the inradius.
R = 2r
The circumradius R is equal to 2 times the inradius r
You might also be interested in our right triangle calculator.