Triangle Area Calculator
Find the area of a triangle using the base and height, three sides, two sides & one angle, or two angles & one side with the triangle area calculator.
Triangle Area:
On this page:
- Triangle Area Calculator
- How to Find the Area of a Triangle
- Base and Height Method
- Three Sides Method
- Side-Angle-Side Method
- Side-Side-Angle Method
- Angle-Side-Angle Method
- Angle-Angle-Side Method
- Equilateral Triangle Area
- Right Triangle Area
- Law of Sines and Law of Cosines
- Law of Sines
- Law of Cosines
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
Zach is a former math teacher with a Master's degree in education and a Bachelor's degree in mathematics, and is currently pursuing his PhD.
How to Find the Area of a Triangle
A triangle is a two-dimensional shape with three straight sides and three interior angles created by the intersection of any two of the sides. You can find the area of a triangle using a few formulas and a little trigonometry, depending on which parts of the triangle you know.
The most common ways are using the base and height, SSS, SAS, SSA, ASA, or AAS methods. The method you choose depends on which side lengths or angles you know.
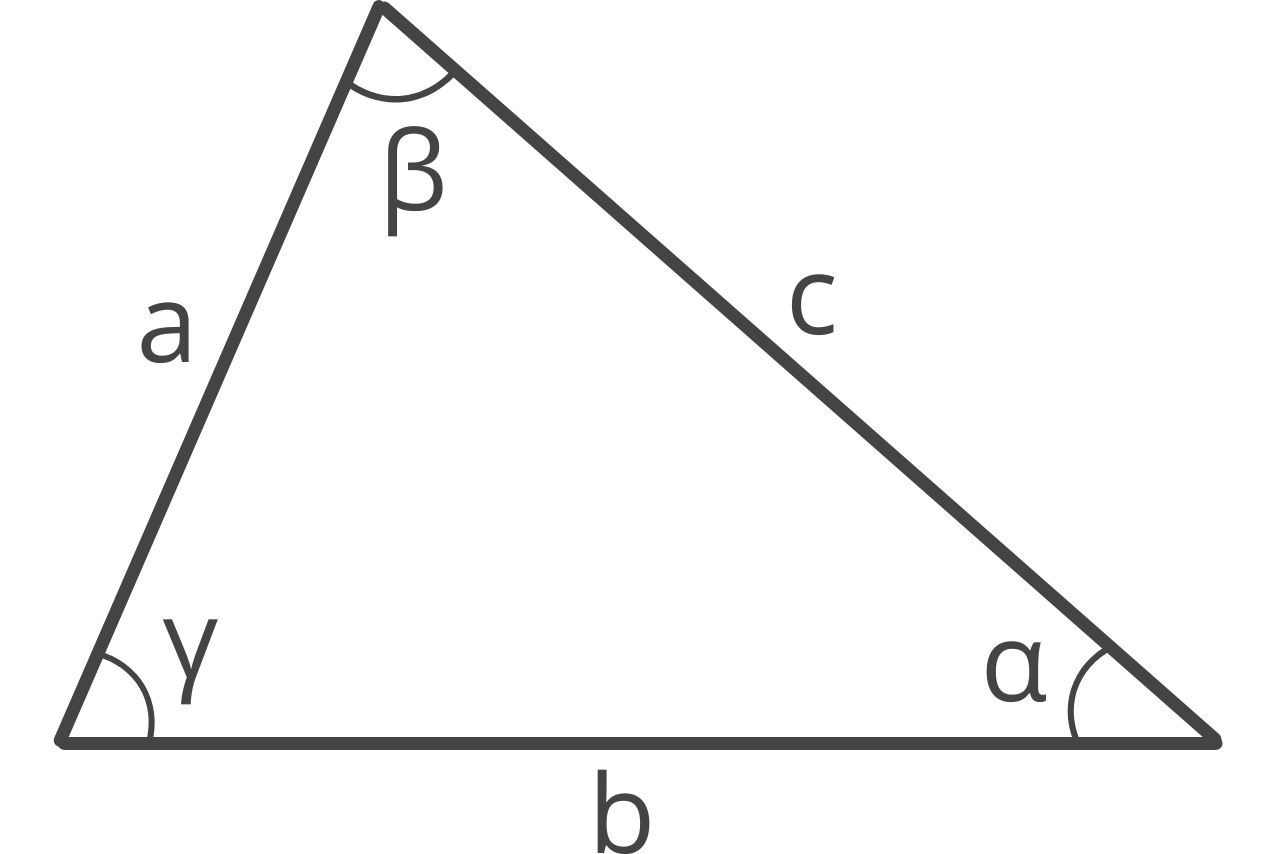
You can find the area of a triangle using a formula. The one you choose will vary depending on what you know about the triangle, but we’ll cover the most commonly used formulas below.
There are several types of triangles (six in fact!), and some of them also have special formulas to find their area.
Base and Height Method
The base and height method is the most commonly used and taught method to find the area of a triangle. Any side can be the base of the triangle, and the height, or altitude, is the perpendicular length from the base to its opposing vertex.
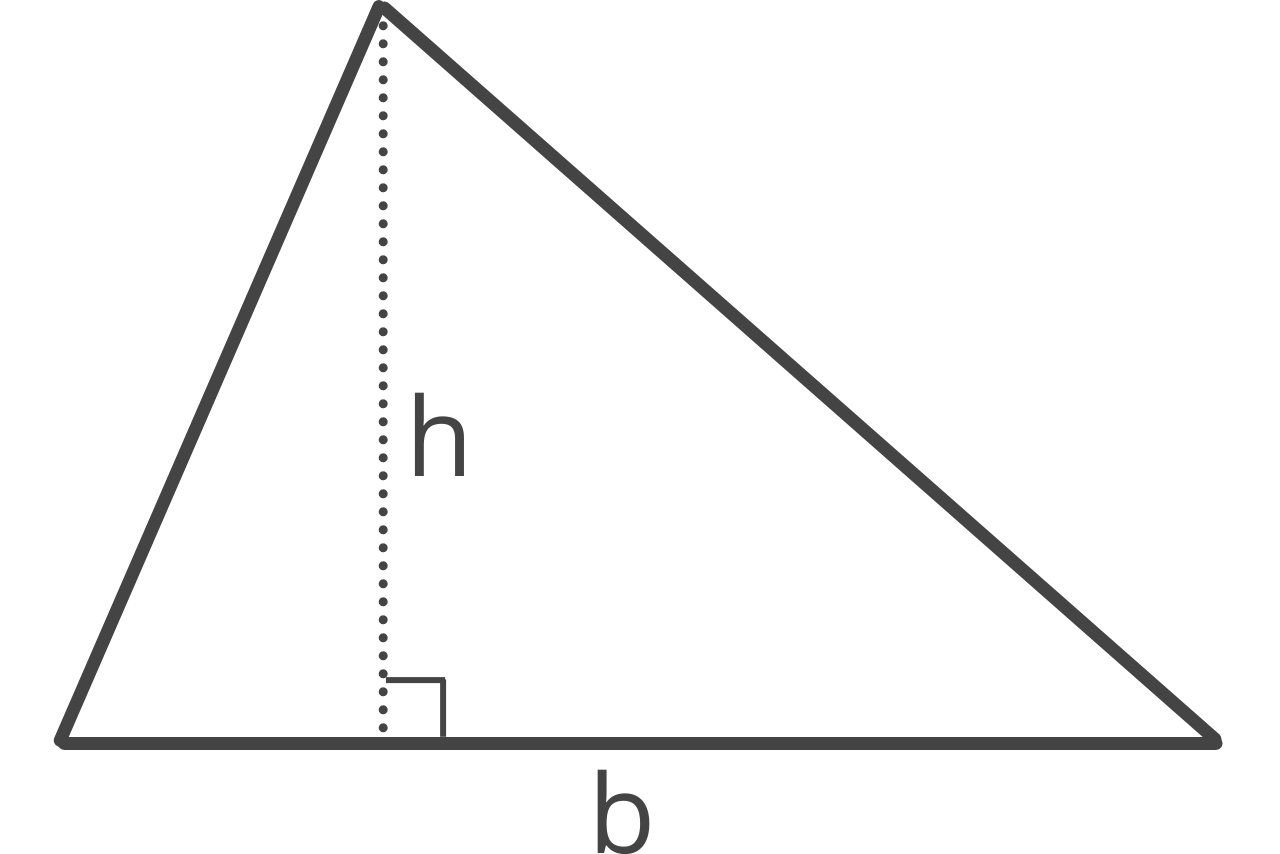
Given the base and height, the formula to find the area of the triangle is:
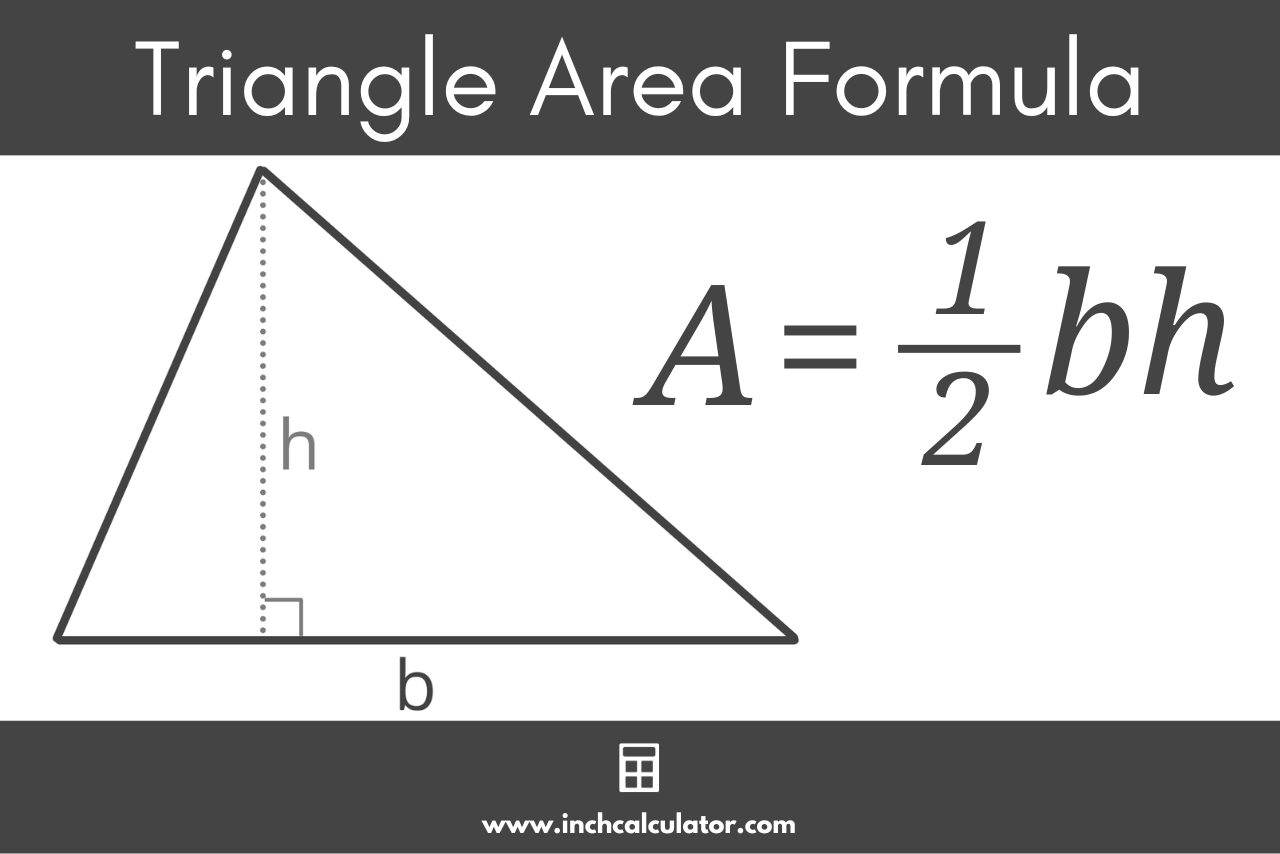
area = 1 / 2bh
The triangle area is equal to 1/2 times base b times height h.
Three Sides Method
The three sides method (SSS or side-side-side) is a method of finding a triangle’s area using the length of all three sides. This method is also known as Heron’s formula.
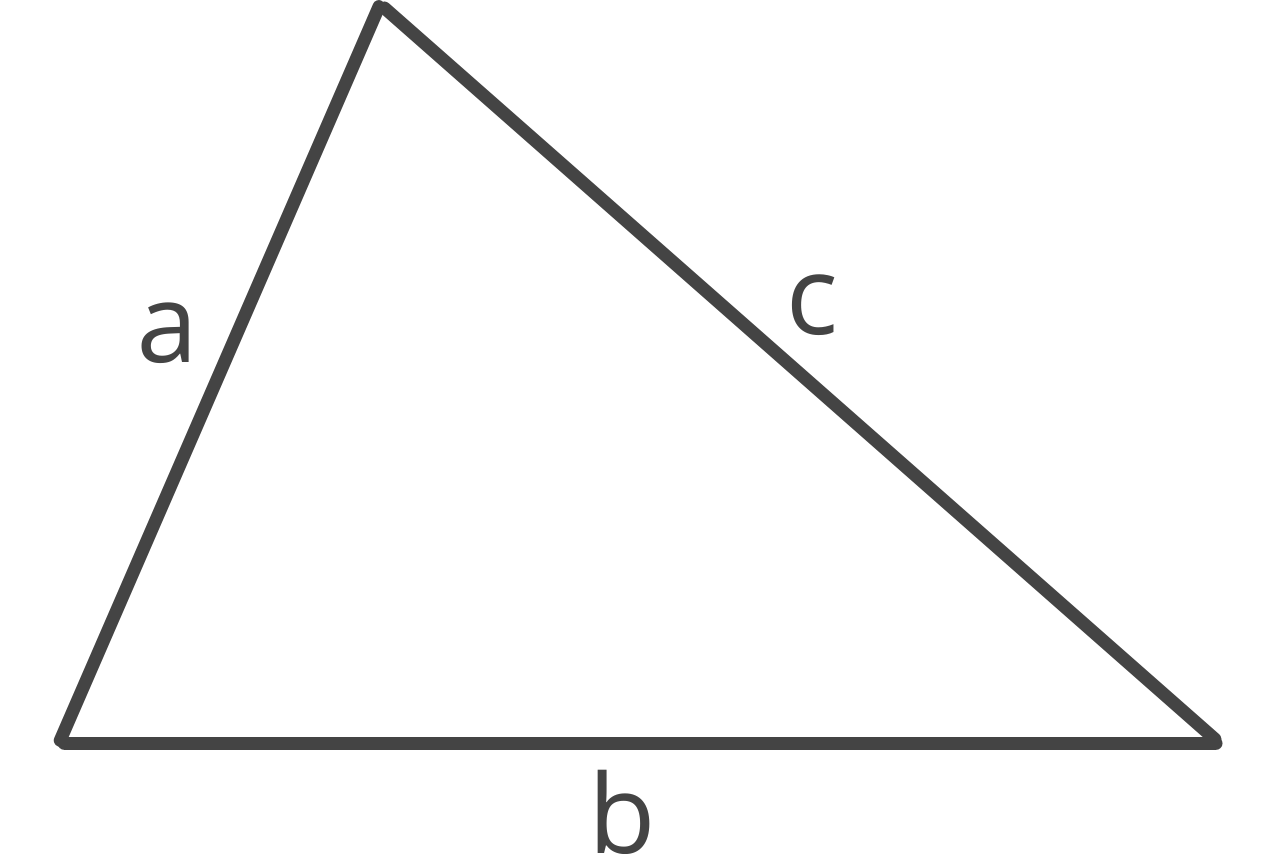
Given the length of all three sides of a triangle, the steps to find its area are to find the semiperimeter, then apply Heron’s formula.
The semiperimeter is half of the perimeter. The formula to find the semiperimeter of the triangle is:
s = a + b + c / 2
The semiperimeter s is equal to side a plus side b plus side c, divided by 2. Put more simply, the semiperimeter is half the perimeter. You can also use our perimeter calculator to find this.
Heron’s formula to find the area is:
area = s(s – a)(s – b)(s – c)
Heron’s formula states that the area of a triangle is equal to the square root of the semiperimeter s times s minus side a times s minus side b times s minus side c.
Side-Angle-Side Method
The side-angle-side (SAS) method allows you to find the area of a triangle if you know the length of two sides and the angle between them.
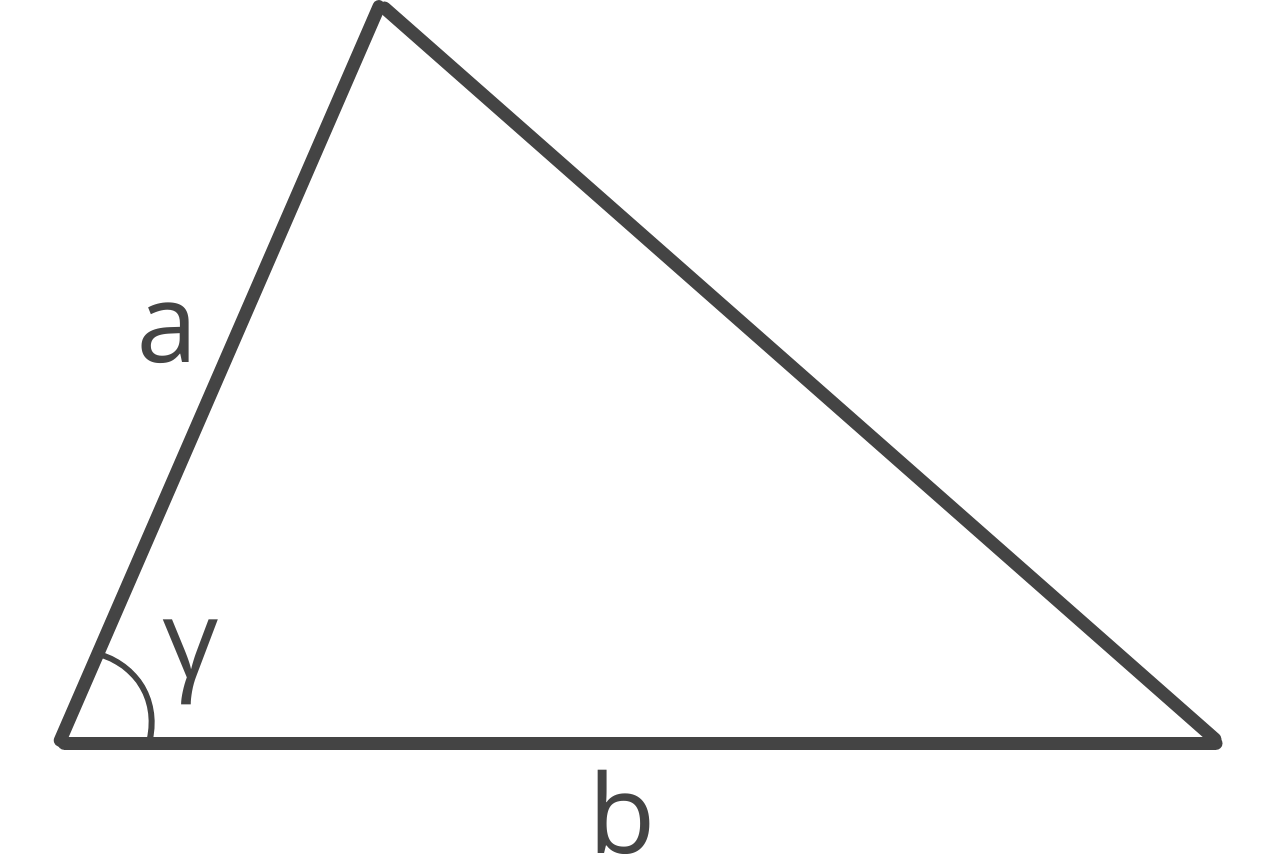
Given the length of two sides and the angle between them, the SAS formula to find the area is:
area = 1 / 2ab × sin(γ)
The area is equal to 1/2 the length of side a times side b, times the sine of the adjoining angle γ.
Side-Side-Angle Method
The side-side-angle (SSA) method is similar to the SAS method, but it allows you to find the area of a triangle if you know the length of two sides and an angle that is not between them.
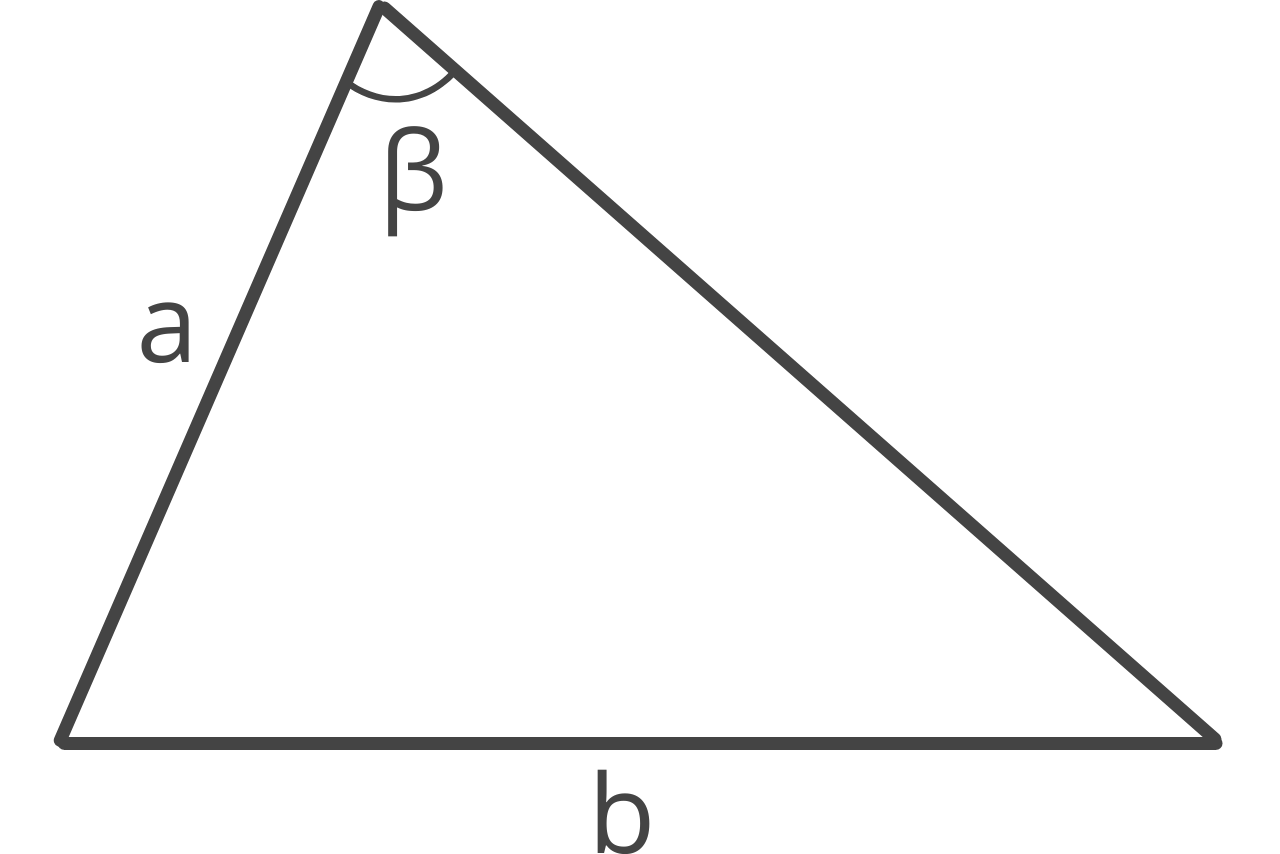
The steps to find the area using the SSA method are to first find the remaining angles using a formula derived from the Law of Sines, then use the SAS method above.
Note, angle α represents the angle opposite of side a and angle β represents the third interior angle between a and b.
α = arcsin(a × sin(β) ÷ b)
γ = 180 – α – β
area = 1 / 2ab × sin(γ)
This method takes advantage of a special rule where the interior angles of a triangle must equal 180°. So to find the third angle, the known angles are subtracted from 180°.
Angle-Side-Angle Method
The angle-side-angle (ASA) method can be used to find area if you know the length of one side and the two adjacent angles.
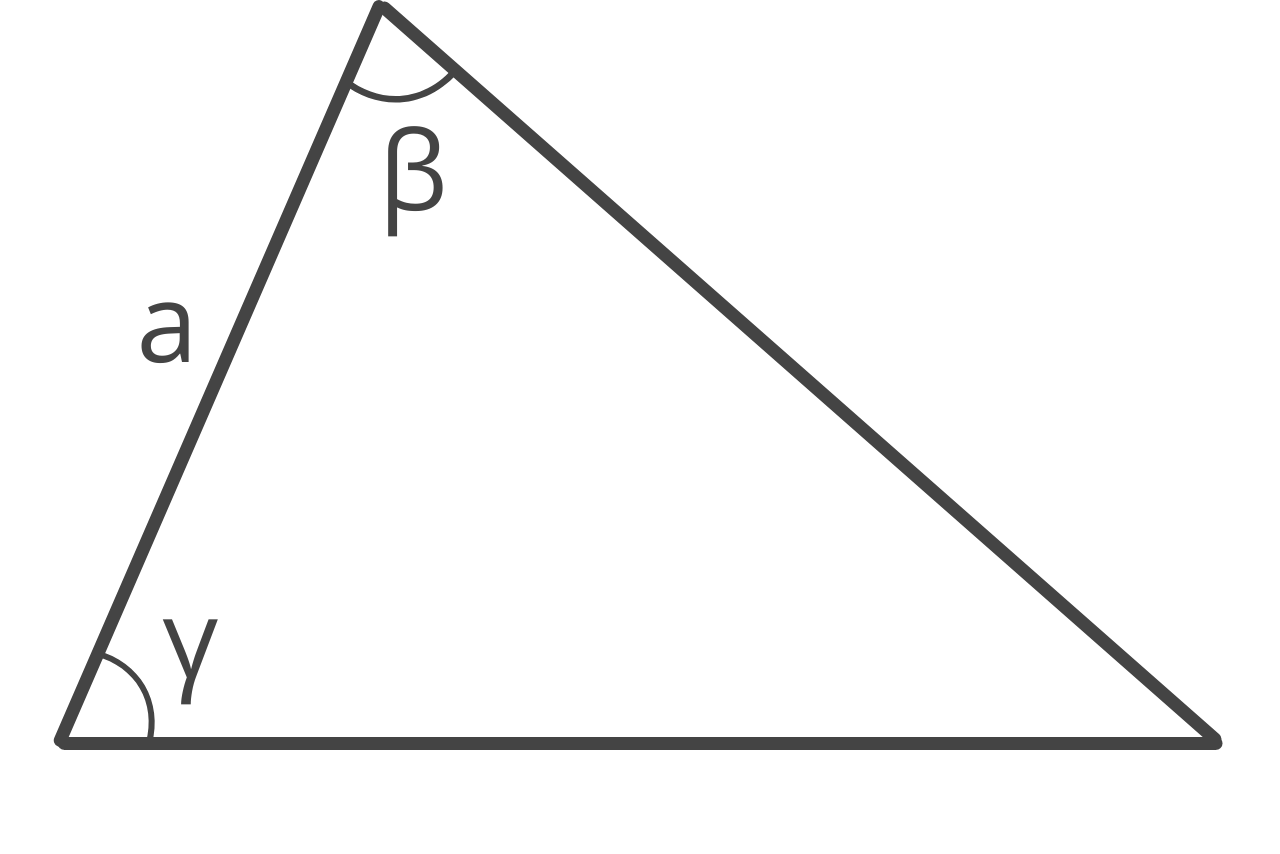
Given the length of one side and the adjacent angles, the steps to find the area are to first find the remaining angle, then use one of the angles to find the height h, then use the Law of Sines to find the base b, and finally use the base and height formula.
Note, angle α represents the angle opposite of side a, and b represents the side opposite angle β.
α = 180 – β – γ
h = a × sin(γ)
b = a × sin(β) ÷ sin(α)
area = 1 / 2bh
Angle-Angle-Side Method
The angle-angle-side (AAS) method can be used to find the area if you know the length of one side, the opposing angle, and one adjacent angle.
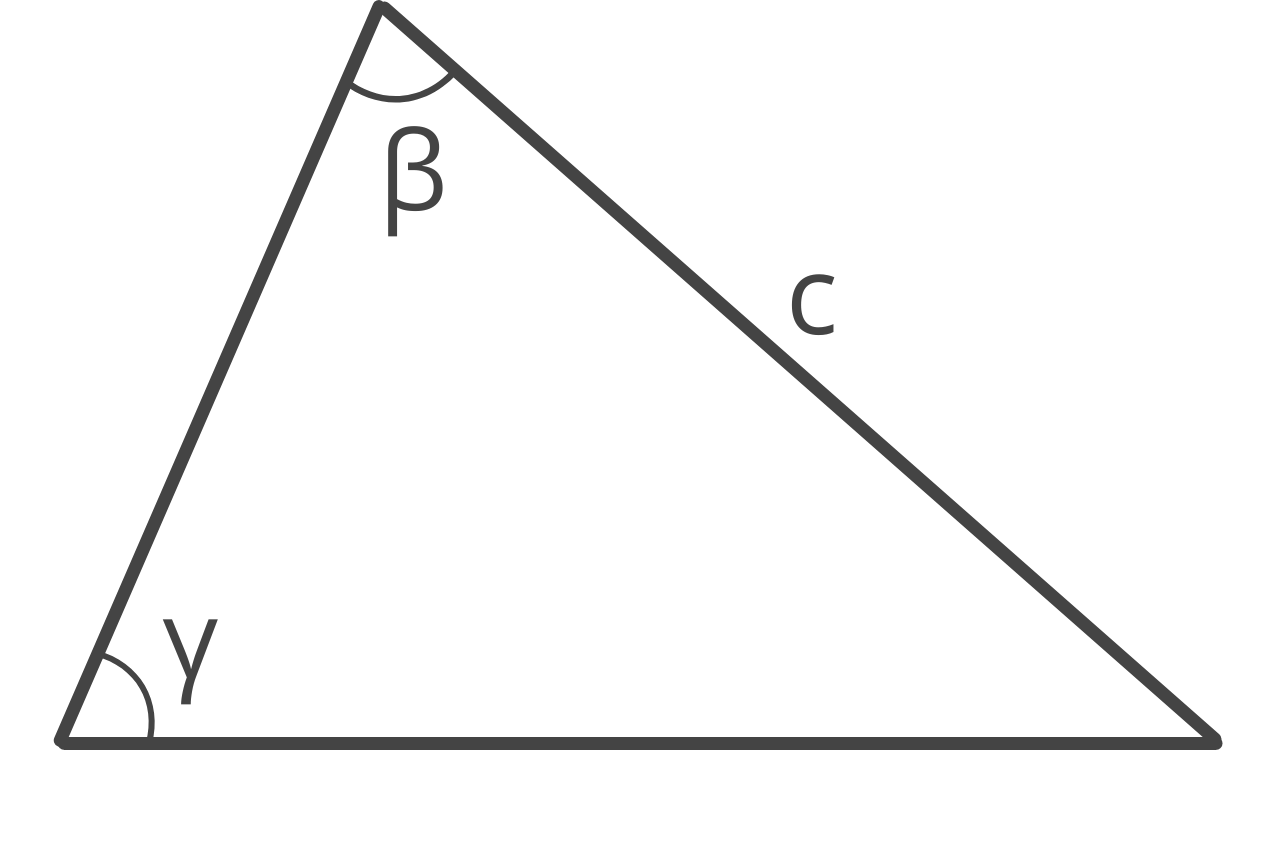
The steps to find the area using the AAS method are to first find the remaining angle, then use the Law of Sines to find the length of the remaining two sides, then find the height h, and finally, use the base and height formula.
Note, angle α represents the third interior angle adjacent to side c, and a represents the side opposite angle α.
α = 180 – β – γ
b = c × sin(β) ÷ sin(γ)
a = c × sin(α) ÷ sin(γ)
h = a × sin(γ)
area = 1 / 2bh
Equilateral Triangle Area
An equilateral triangle is one where all three sides are equal in length, and all three angles are 60°. Given an equilateral triangle, you can find the area using the length of one of the sides.
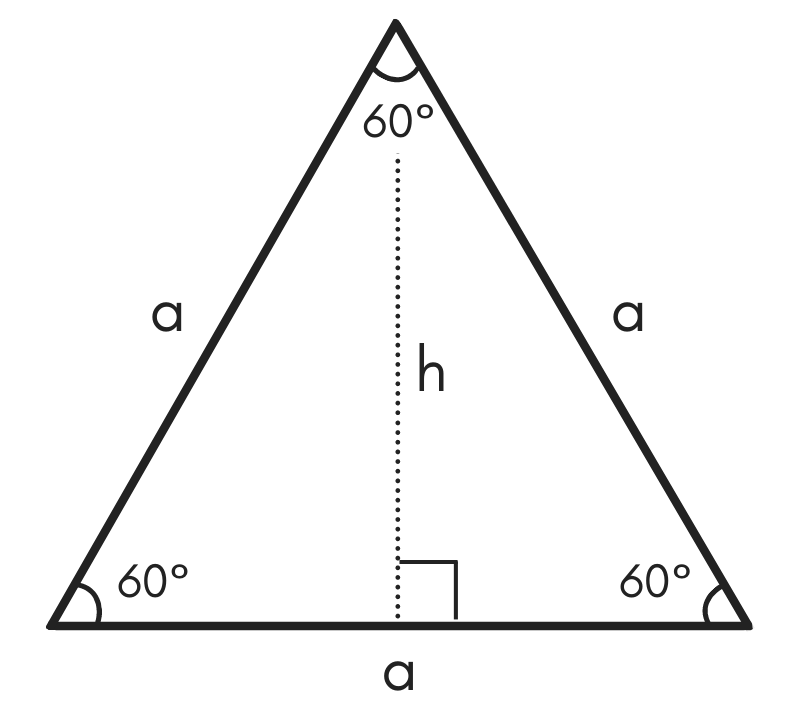
The formula to find the area for an equilateral triangle is:
area = √3 / 4a²
The area of an equilateral triangle is equal to the square root of 3 divided by 4, times the length of side a squared.
Right Triangle Area
A right triangle is a triangle that has one 90° angle. Given a right triangle, you can find the area using a few special methods.
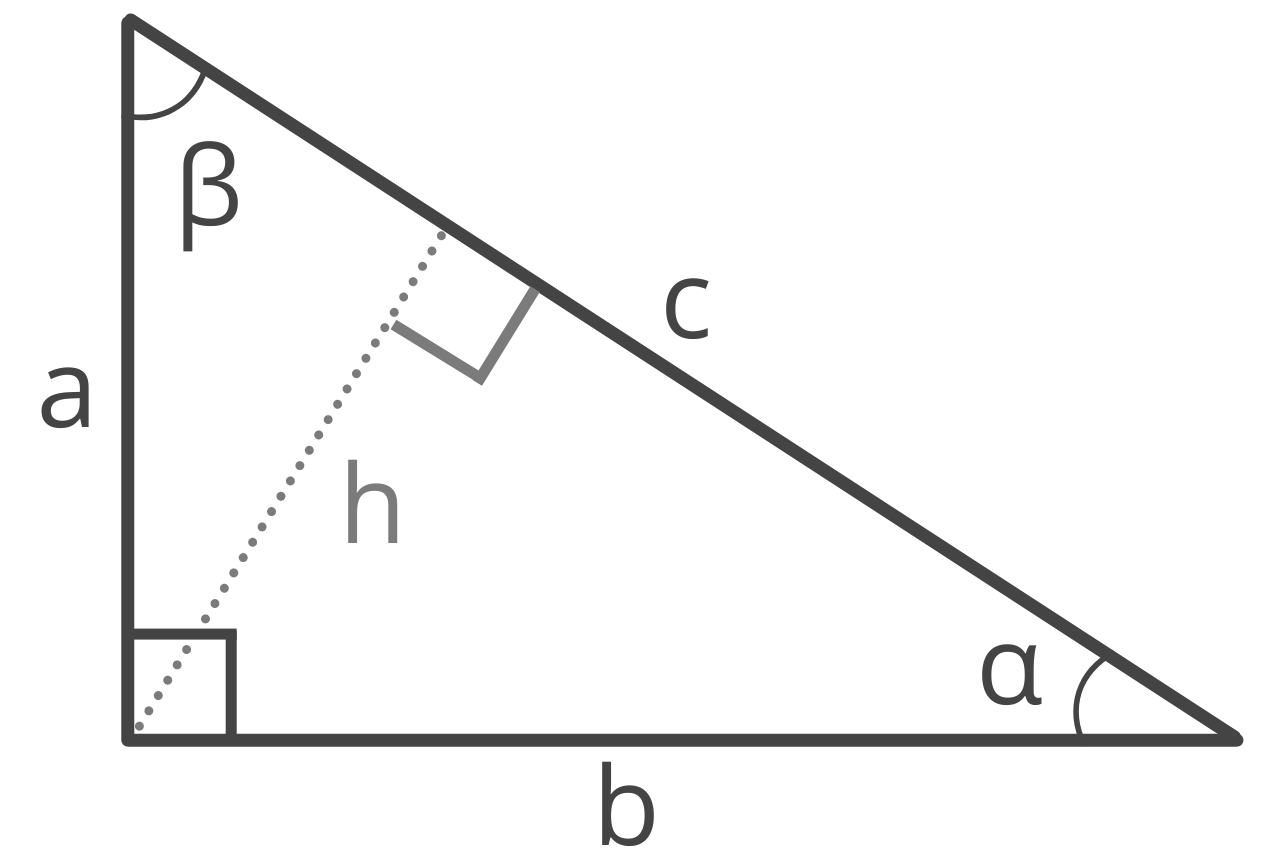
Method One: Given Two Legs
The first method is to use the length of the two sides adjacent to the right angle using this formula:
area = 1 / 2ab
The area of a right triangle is equal to 1/2 times side a times side b. Since a right angle is essentially a rectangle divided in half diagonally, think of this method as calculating the area of a rectangle, then dividing it in half.
Method Two: Given Leg & Hypotenuse
The second method to find the area of a right triangle is to use the hypotenuse and the length of one of the other sides with a variation of the Pythagorean theorem formula:
area = a × 1 / 2c² – a²
The area of a right triangle is equal to the length of side a times 1/2 times the square root of the length of the hypotenuse c squared minus side a squared.
Method Three: Given Leg and Angle
If you know the length of one leg and the value of an adjacent angle in a right triangle, then you can find the area using the tangent function.
Given leg a and angle β, find the area with the formula:
area = a² × tan(β) / 2
The area of a right triangle is equal to side a squared times the tangent of angle β, divided by 2.
Law of Sines and Law of Cosines
Many of the formulas used to find the area of a triangle make use of the Law of Sines and the Law of Cosines in some way.
Law of Sines
The Law of Sines, also called the Sine Rule, defines the relationship between the side lengths of a triangle and their opposing angles. The Law of Sines is defined by the following formula:
a / sin α = b / sin β = c / sin γ
The Law of Sines states that side a divided by the sine of its opposing angle α is equal to side b divided by the sine of its opposing angle β, which and also equal to side c divided by the sine of its opposing angle γ.
Law of Cosines
The Law of Cosines, also called the Cosine Rule, defines the relationship between the side lengths of a triangle to the cosine of one of the angles. The Law of Cosines is a generalization of the Pythagorean theorem.
The Law of Cosines is defined by the following formula:
c² = a² + b² – 2ab cos γ
a² = b² + c² – 2bc cos α
b² = a² + c² – 2ac cos β
The Law of Cosines states that side c squared is equal to side a squared plus side b squared, minus 2 times side a times side b times the cosine of the opposing angle γ.
Find the area of many other shapes using our area calculator.