Heron’s Formula Calculator
Enter the three sides of a triangle to calculate the area using Heron’s formula.
Solution:
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
Zach is a former math teacher with a Master's degree in education and a Bachelor's degree in mathematics, and is currently pursuing his PhD.
How to use Heron’s Formula
Using Heron’s formula is an easy way to calculate the area of a triangle given the length of the sides. The most commonly used formula for the area of a triangle requires knowing the height of the triangle, which often requires knowing the interior angles to determine.
However, Heron’s formula does not require knowing the height of the triangle. Thus, the interior angles of the triangle are not needed to find area using this formula.
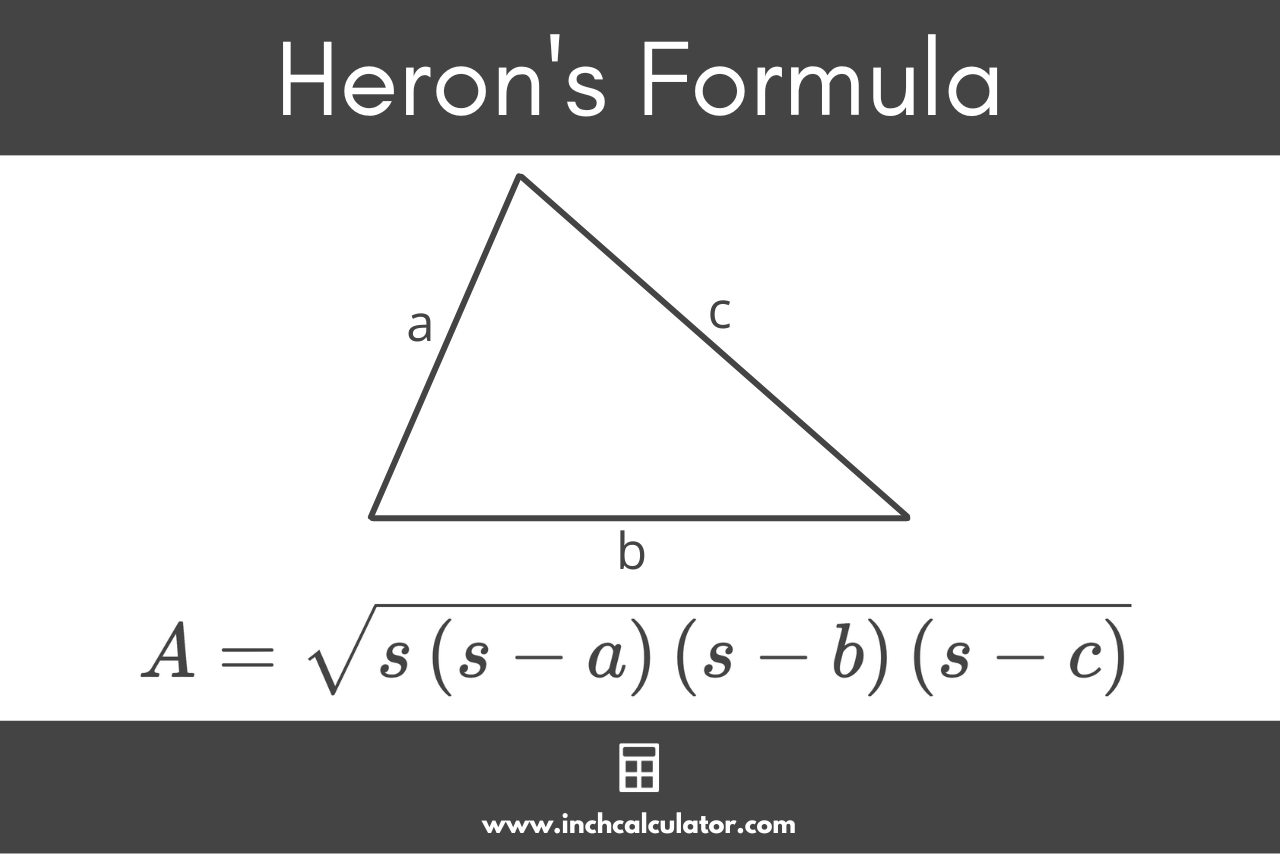
For a triangle with three side lengths a, b, and c, and the semiperimeter s, Heron’s formula can be used to find the area.
A = s(s – a)(s – b)(s – c)
Thus, the area A of a triangle is equal to the square root of the semiperimeter s times s minus side a times s minus side b times s minus side c .
The semiperimeter s in Heron’s formula is half the perimeter, so the equation to find s is:
s = a + b + c / 2
The semiperimeter s is equal to the quantity side a plus side b plus side c, divided by 2.
After solving the semiperimeter, substitute s in Heron’s formula above, along with side lengths a, b, and c, to solve for the area.
Alternate Heron’s Formula Equations
Heron’s formula can be simplified or rewritten in a few different ways to solve for area. The following formulas are all derived from Heron’s formula with respect to side lengths a, b, and c.
A = 1 / 4(a + b + c)(-a + b + c)(a – b + c)(a + b – c)
A = 1 / 42(a²b² + a²c² + b²c²) – (a⁴ + b⁴ + c⁴)
A = 1 / 4(a² + b² + c²)² – 2(a⁴ + b⁴ + c⁴)
A = 1 / 44(a²b² + a²c² + b²c²) – (a² + b² + c²)²
A = 1 / 44a²b² – (a² + b² – c²)²