Triangle Height Calculator
Calculate the height of a triangle by entering the base and area dimensions below.
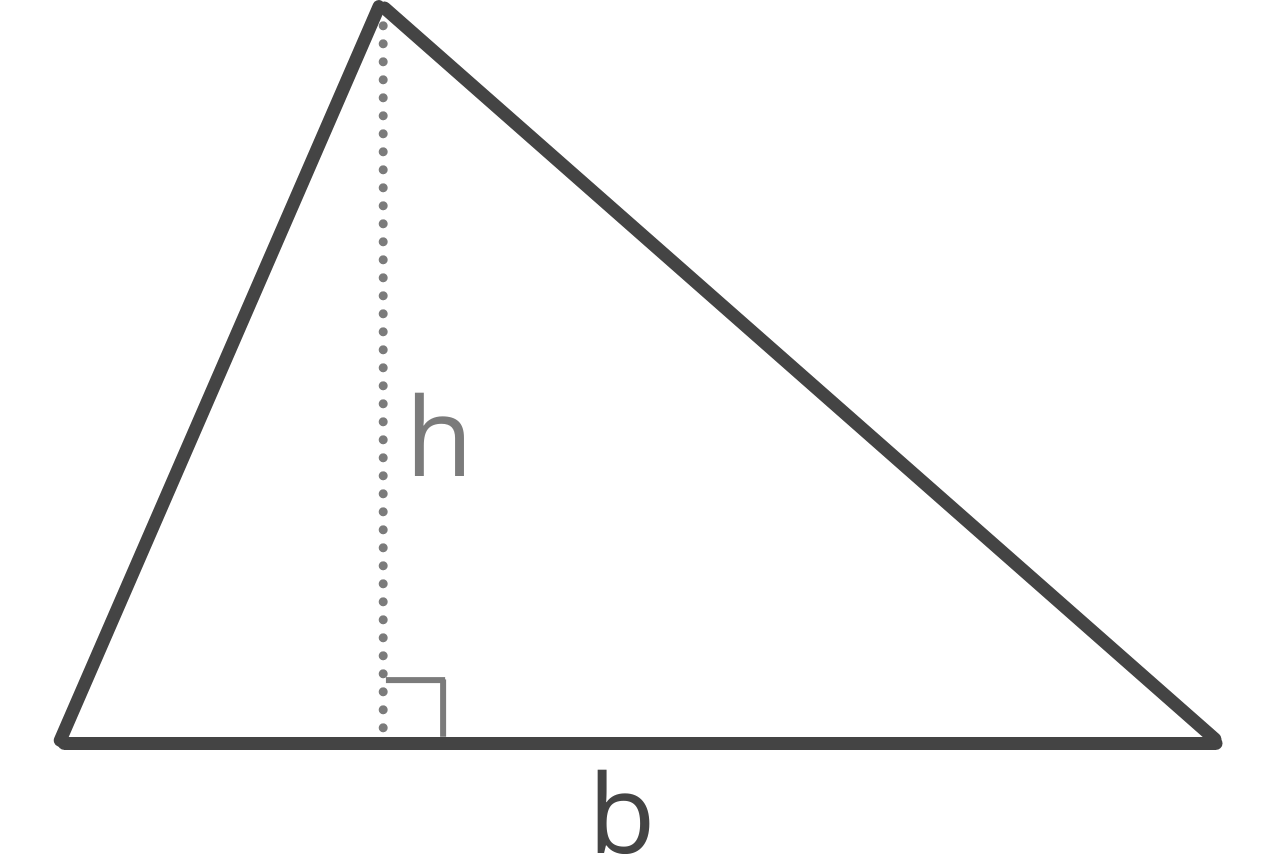
Triangle Height:
On this page:
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
Zach is a former math teacher with a Master's degree in education and a Bachelor's degree in mathematics, and is currently pursuing his PhD.
How to Calculate the Height of a Triangle
Triangle height, also referred to as its altitude, can be solved using a simple formula using the length of the base and the area.
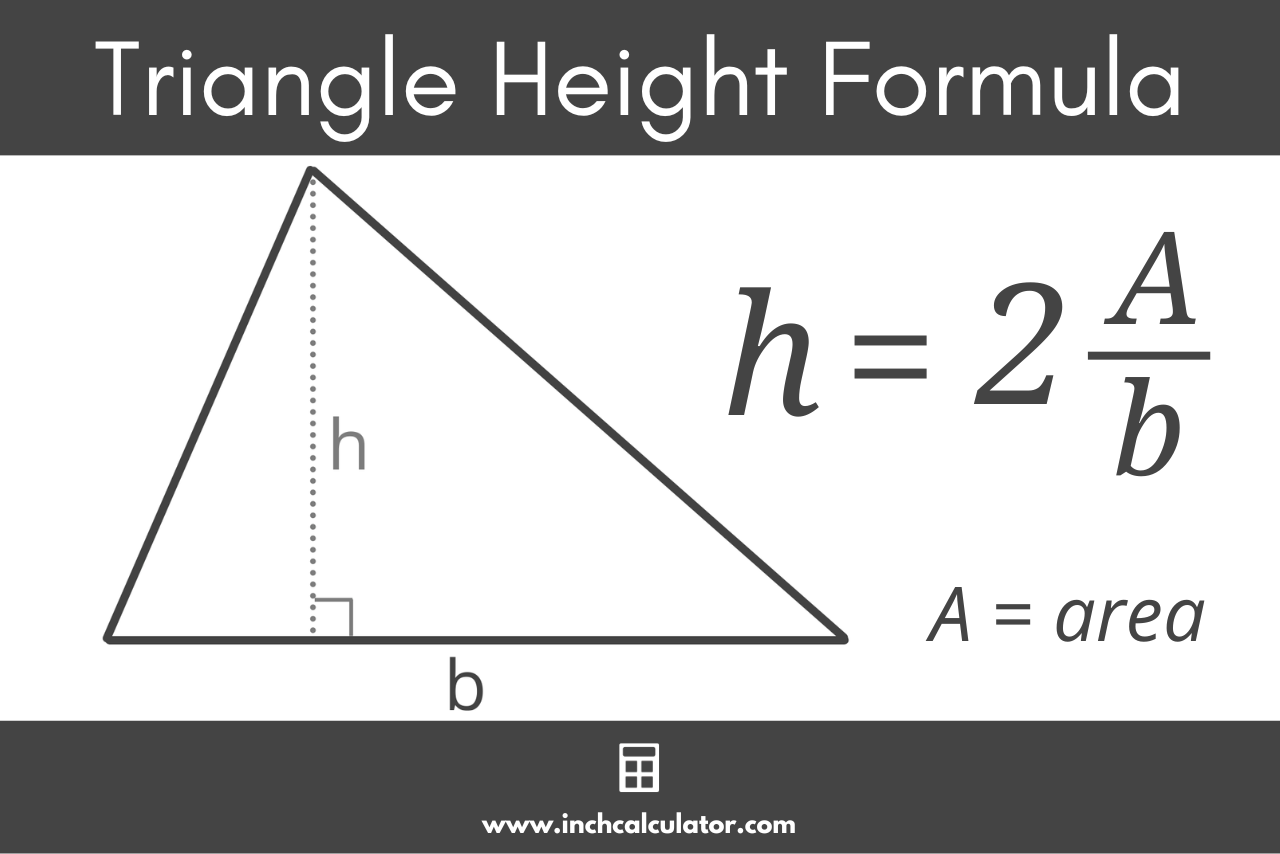
h = 2A / b
Thus, the height or altitude of a triangle h is equal to 2 times the area A divided by the length of base b.
How to Find Triangle Height Without the Area
Given the length of the triangle’s three sides, it is possible to calculate the height by finding the area first. The area of a triangle can be found using Heron’s formula.
The first step is to find the perimeter of the triangle p, which can be found by adding all three side lengths.
p = a + b + c
Then, using the perimeter, solve for the semiperimeter s, which is equal to half the perimeter.
s = p / 2
Finally, use the semiperimeter s and the length of the three sides a, b, and c with Heron’s formula to solve the area of a triangle.
A = s(s – a)(s – b)(s – c)
Thus, the area A of a triangle is equal to the square root of s times s minus a times s minus b times s minus c.
Then, to solve for height, use the area and the base with the formula above. Note, a triangle has three different heights, or altitudes. The height you solve for with the steps above would be the height from the base b to the vertex opposite of base b.
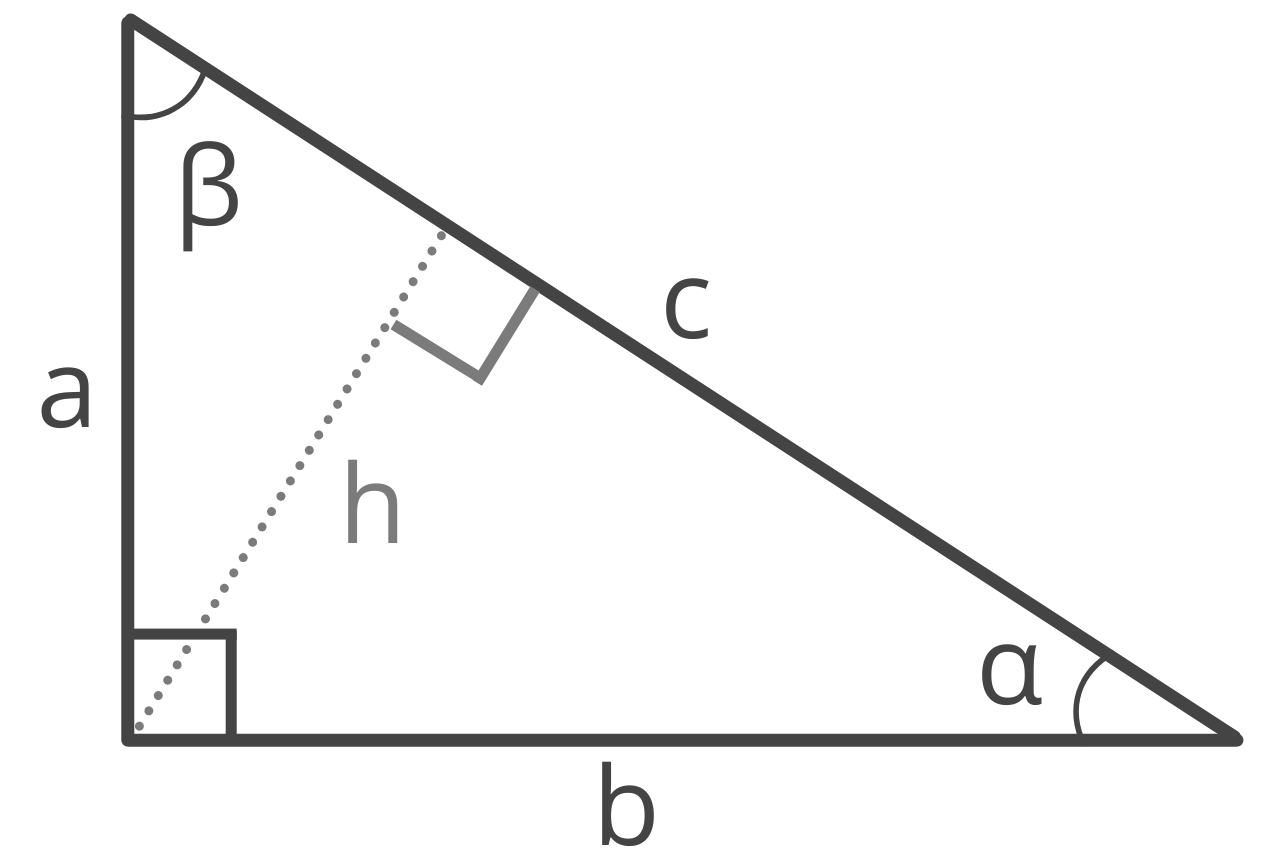
How to Find the Height of a Right Triangle
For a right triangle, there is a simple formula to solve the height, which is derived from the AA theorem and triangle similarity.
h = ab / c
The altitude h of a right triangle is equal to a times b, divided by c.
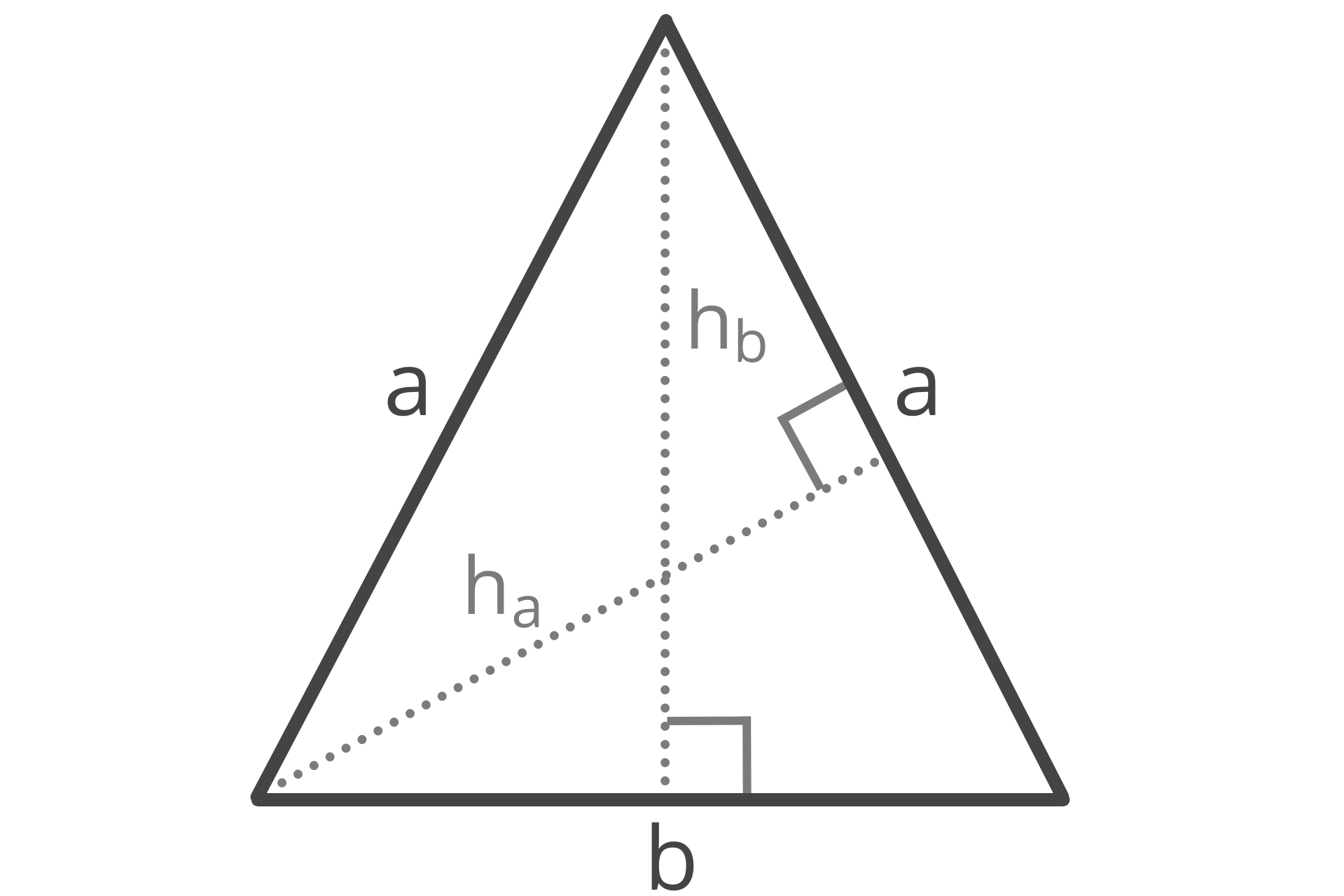
How to Find the Height of an Isosceles Triangle
An isosceles triangle has two distinct heights, the height from base a to the opposite vertex and the height from base b to the opposite vertex. Use the following formulas to solve the heights of each.
ha = √(a² – (0.5 × b)²) × b / a
The altitude ha from base a to the opposite vertex is equal to the square root of a squared minus 0.5 times b, squared, times b, divided by a.
hb = a² – (0.5 × b)²
The altitude hb from base b to the opposite vertex is equal to the square root of a squared minus 0.5 times b, squared.
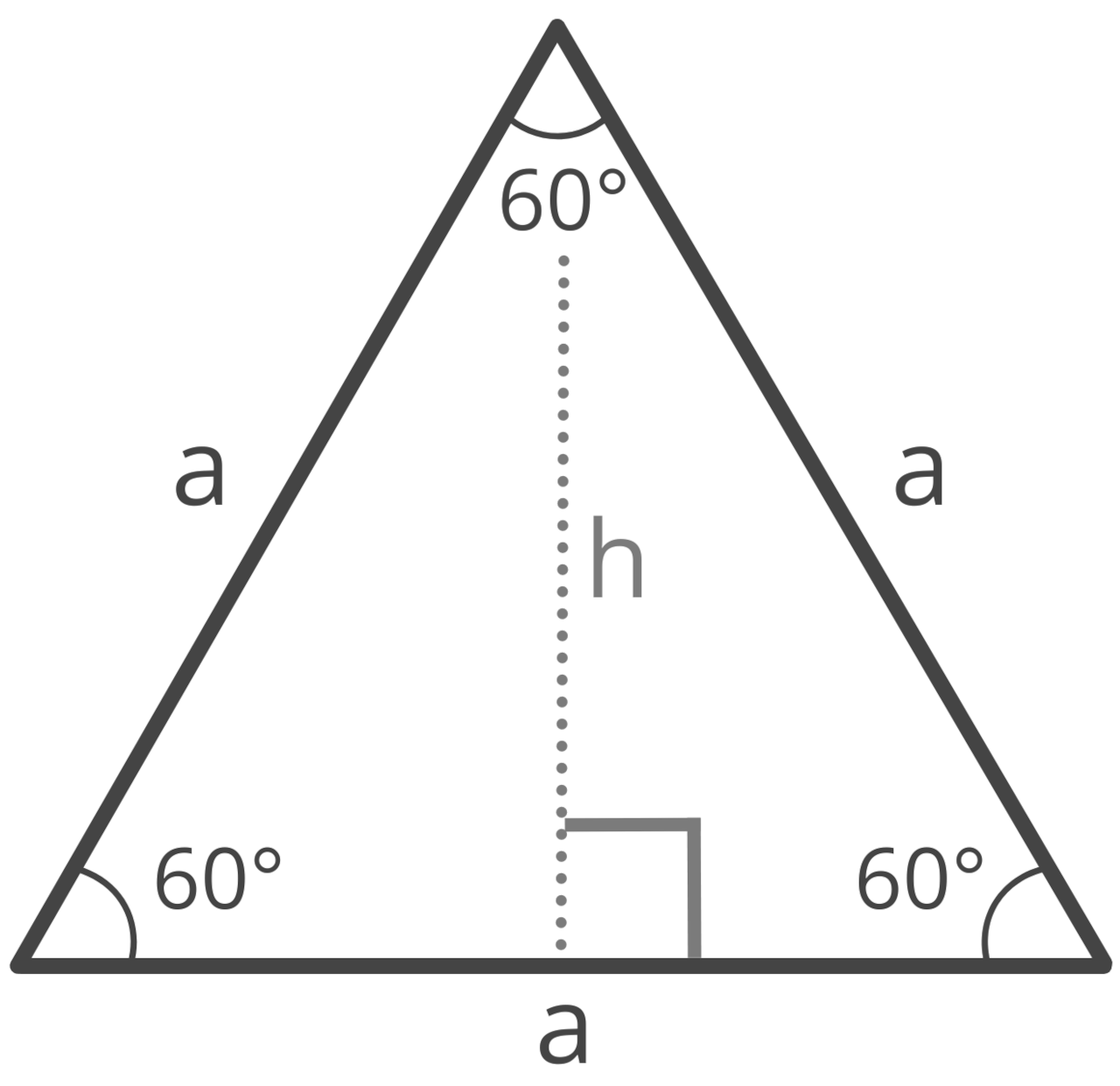
How to Find the Height of an Equilateral Triangle
Since an equilateral triangle has three equal sides and three equal angles, it also has three equal heights. The formula to find the height of an equilateral triangle is:
h = a × √3 / 2
The altitude h is equal to a times the square root of 3, divided by 2.
How to Use the Pythagorean Theorem to Find the Height
You can also find the height of an equilateral triangle using the Pythagorean theorem. Recall that the Pythagorean theorem states that a² + b² = c² for a right triangle.
An equilateral triangle can be divided into two equal right triangles like this:
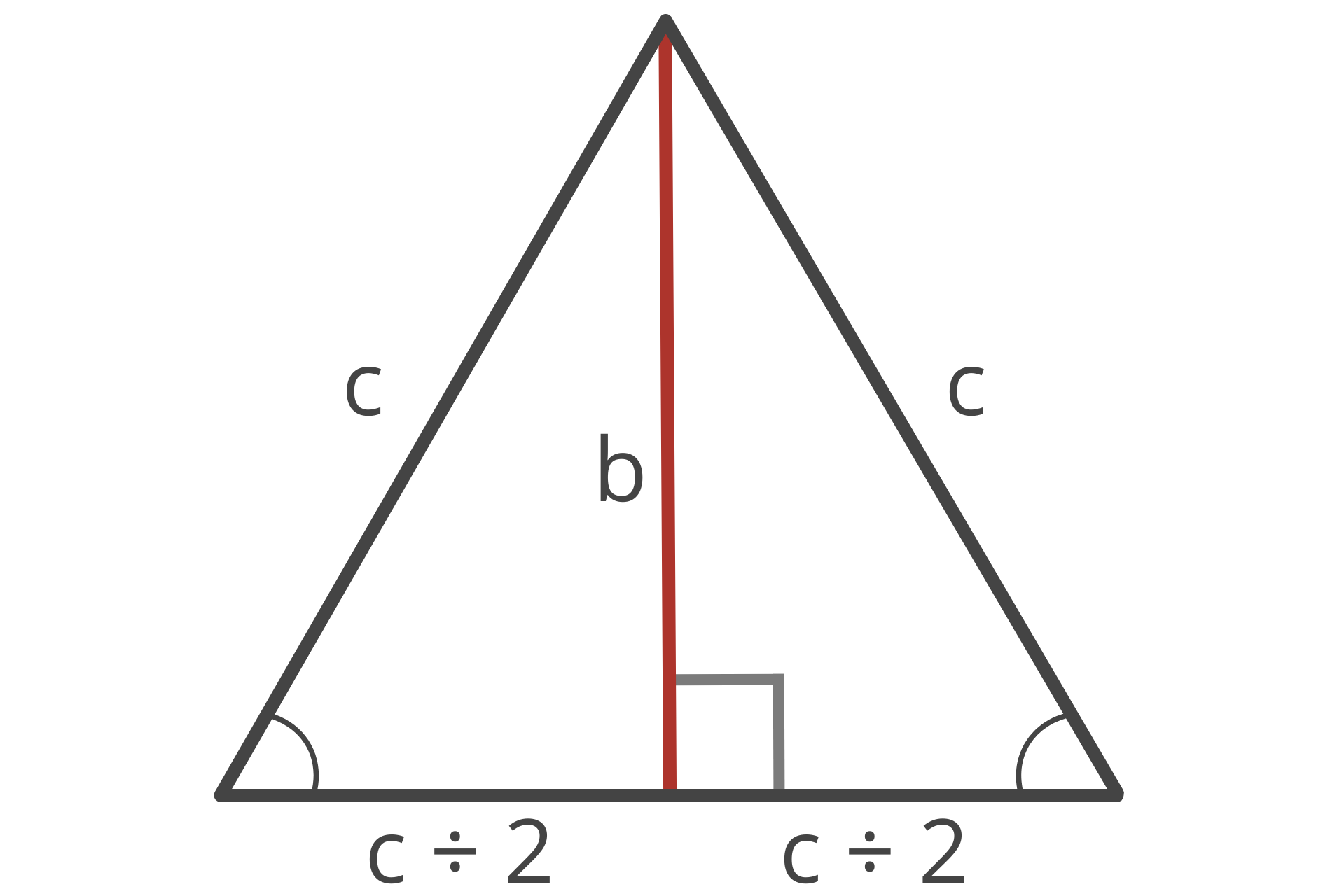
In the right triangles, the hypotenuse c is equal to the length of the equilateral triangle’s sides, side a is then equal to one-half of the hypotenuse, and side b is equal to the equilateral triangle’s height.
So, to solve the height of the equilateral triangle, you can solve for the length of side b in the newly created right triangles using the Pythagorean theorem. The formula looks like this:
(c ÷ 2)² + b² = c²
By rearranging the equation, we can solve for the length of b:
b² = c² – (c ÷ 2)²
b = c² – (c ÷ 2)²
So, the length of b (and the height h of the equilateral triangle) is equal to the square root of the square of the hypotenuse c divided by 2 plus the square of the hypotenuse.