Pythagorean Theorem Calculator
Use the Pythagorean theorem to solve the length of any side of a right triangle or its area by entering known leg or hypotenuse values.
Solution and Steps:
Steps to Solve
Steps to Solve
Steps to Solve
Steps to Solve
On this page:
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
Zach is a former math teacher with a Master's degree in education and a Bachelor's degree in mathematics, and is currently pursuing his PhD.
What is the Pythagorean Theorem?
The Pythagorean theorem, sometimes called Pythagoras’ theorem, is an equation that relates the three sides of a right triangle, the two shorter sides (often called legs), and the longest side, called the hypotenuse.
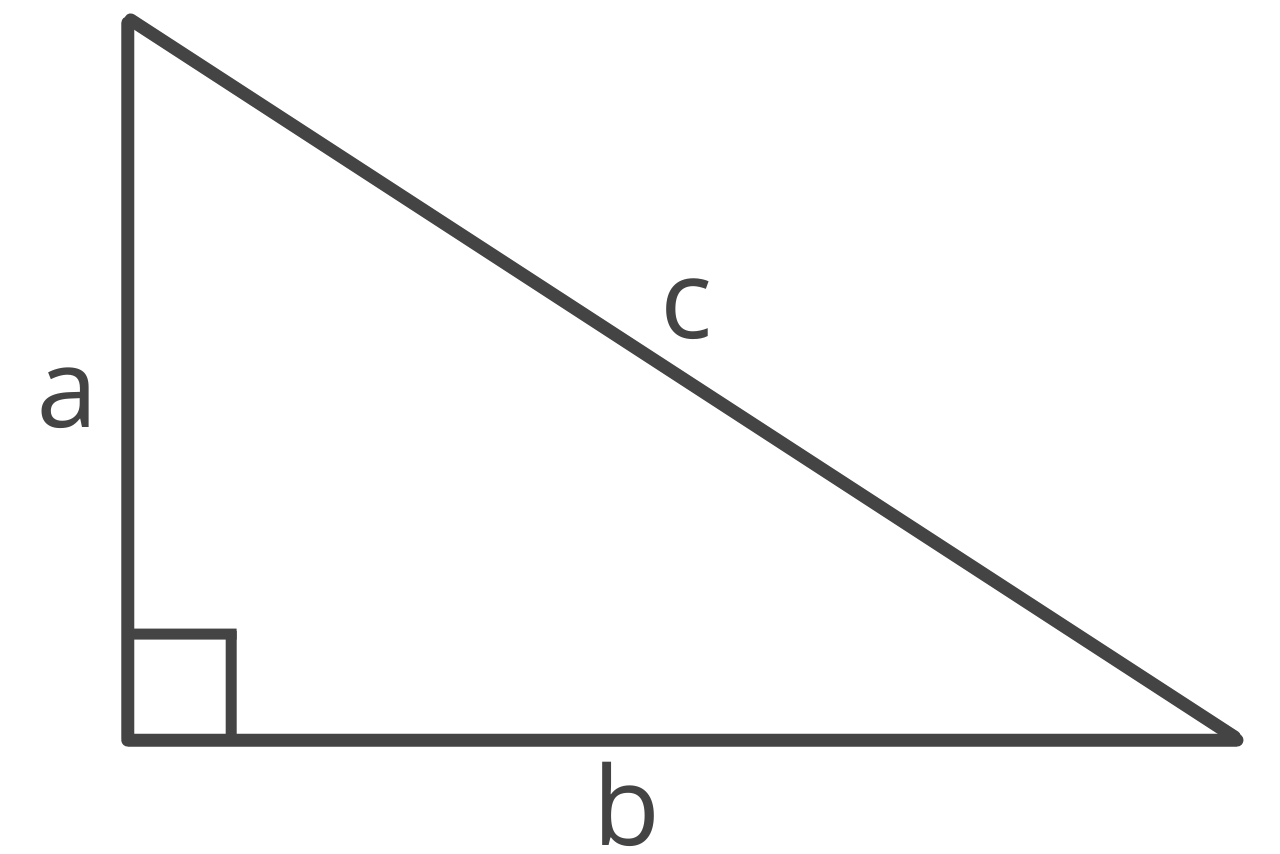
The Pythagorean theorem can be used to solve any side if the length of the other two sides is known.
The Pythagorean theorem states that the length of the hypotenuse squared is equal to the sum of the squares of each leg.
Pythagorean Theorem Formula
The Pythagorean theorem is expressed using the following equation, where a and b are the side lengths of the two legs, and c is the length of the hypotenuse:
a² + b² = c²
Thus, side a squared plus side b squared is equal to the square of the hypotenuse c.
How to use the Pythagorean Theorem for Right Triangles
Given the length of any two sides of a right triangle, the Pythagorean theorem is used to solve the length of the third side. To solve, replace the values of a, b, or c in the formula with the two known values and solve the equation.
The following formulas are derived from the Pythagorean theorem to solve for any side of a right triangle.
Find the Length of Leg a
The length of leg a can be found using the following formula:
a = c² – b²
The length of leg a is equal to the square root of c squared minus b squared.
Find the Length of Leg b
The length of leg b can be found using the following formula:
b = c² – a²
The length of leg b is equal to the square root of c squared minus a squared.
Find the Length of Hypotenuse c
The length of hypotenuse c can be found using the following formula:
c = a² + b²
The hypotenuse c is equal to the square root of a squared plus b squared.
Inverse Pythagorean Theorem
While the Pythagorean theorem relates the lengths of each side, the Inverse Pythagorean Theorem (sometimes called the Reciprocal Pythagorean Theorem) relates the side lengths to the height, or altitude, to the hypotenuse of a right triangle.
Since sides a and b are equal to the heights of the other side, the inverse Pythagorean theorem defines the relationship between the short sides and the height perpendicular to the hypotenuse.
The Inverse Pythagorean theorem states that if a right triangle with vertices A, B, and C is divided into two triangles by its height h at point D along side c, then the area of △ABC is equal to the area of △ACD plus the area of △BCD.
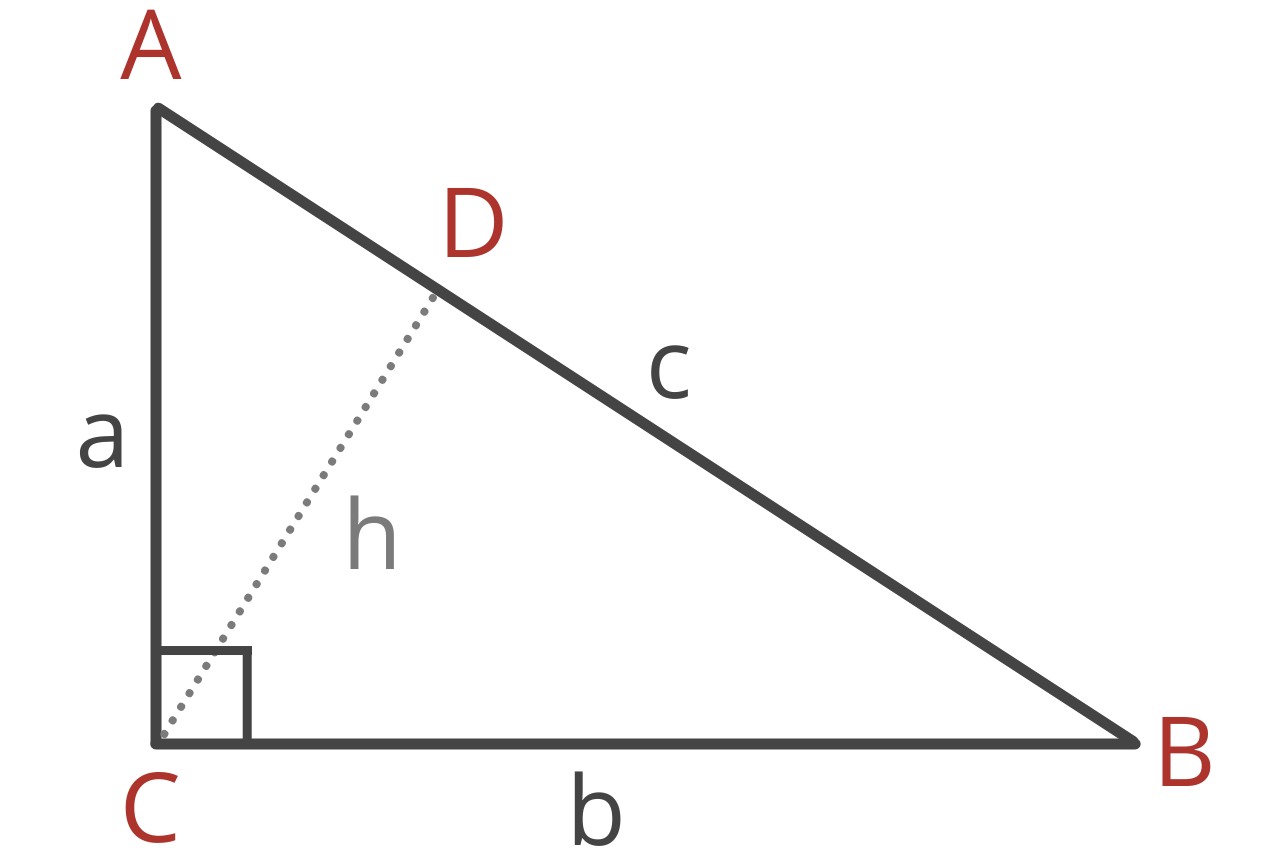
The length of the sides of these new triangles can be defined using the Pythagorean Theorem as follows:
1 / AC² + 1 / BC² = 1 / CD²
Note, AC, BC, and CD represent the length of the line segments connecting the respective vertices. This can be rewritten to more simply express the height of a right triangle:
1 / a² + 1 / b² = 1 / h²
Thus, the Inverse Pythagorean theorem says that the reciprocal of side a squared plus the reciprocal of side b squared is equal to the reciprocal of height h squared.
This can be further reduced to solve for the height given sides a, b, and c.
hc = ab
c = ab / h
You can also use our right triangle calculator to calculate the angles, area, or perimeter.
Pythagorean Triangles
A Pythagorean triangle is a special right triangle where each side length is a whole number. This is also called a Pythagorean triple.
The smallest Pythagorean triple is one with sides of lengths 3, 4, & 5. A primitive Pythagorean triple is a Pythagorean triple where the largest common divisor between them is 1.
For instance, the Pythagorean triple (3, 4, 5) is considered primitive since the largest common divisor is 1. On the other hand, the triple (9, 12, 15) is not primitive since the largest common divisor is 3.
Interestingly, both the area and inradius of a Pythagorean triple will also be whole numbers.
Some other examples of special right triangles are the 30 60 90 right triangle and the 45 45 90 right triangle.