30 60 90 Triangle Calculator
Enter any known value for a 30 60 90 triangle to calculate the edge lengths, altitude, area, perimeter, inradius, and circumradius.
Triangle Properties:
| leg a: | 3
|
| leg b: | 5.196
|
| hypotenuse c: | 6
|
| height h: | 2.598
|
| area: | 7.794
|
| perimeter: | 14.196
|
| inradius: | 1.098
|
| circumradius: | 3
|
On this page:
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
Zach is a former math teacher with a Master's degree in education and a Bachelor's degree in mathematics, and is currently pursuing his PhD.
What is a 30 60 90 Triangle?
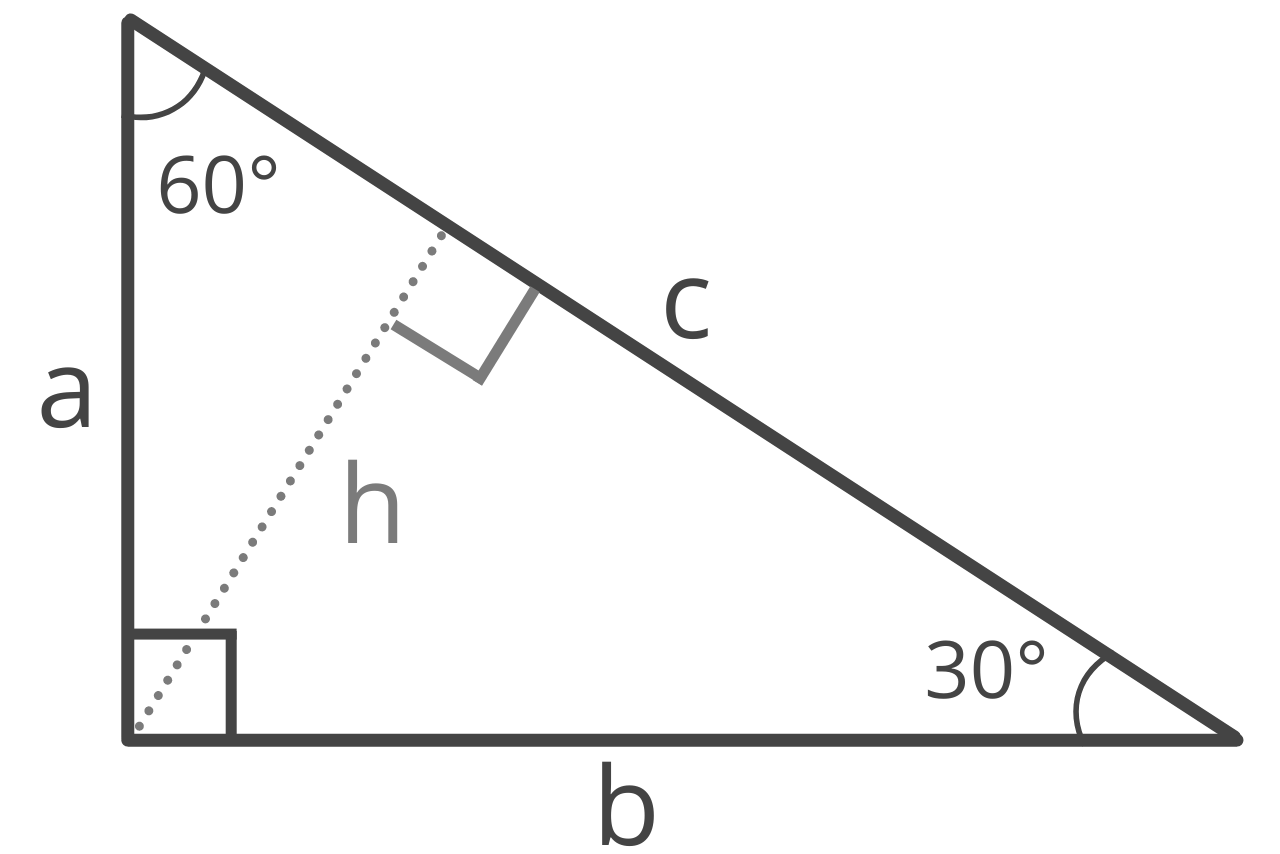
A 30 60 90 triangle is a special right triangle that has interior angles measuring 30°, 60°, and 90°.
You can think of a 30 60 90 triangle as half of an equilateral triangle divided from any vertex to the midpoint of the opposite side.
Like all triangles, the side lengths of a 30 60 90 triangle correspond with the size of the angle opposite the side. The shortest side length will therefore be opposite the 30° angle, and the longest side length, also called the hypotenuse for all right triangles, will be opposite the 90° angle.
Formulas to Solve a 30 60 90 Triangle
Because a 30 60 90 triangle is a right triangle, you can use formulas such as the Pythagorean theorem on them. However, there are also a few simplified formulas that can be used on a 30 60 90 triangle as well, which allow you to solve for unknown side lengths given only one side.
The phrase “solving a triangle” typically refers to using given information to find unknown side lengths and angles.
The sides of a 30 60 90 right triangle will always have a ratio of 1 : √3 : 2. Keep in mind this ratio is structured as a : b : c, where a is the shortest side length (often called a leg), b is the second shortest side length (also often called a leg), and c is the longest side length (called the hypotenuse).
Using this ratio, you can solve for any side length if you know just one of the other side lengths.
Using these ratios is a shortcut to using the known angles and the sine or cosine functions to solve the length of the sides.
Find Leg A
Leg a is the shortest side opposite the 30° angle. Given the length of leg b or the hypotenuse c, the formulas to solve the length of leg a are:
a = b × √3 / 3
a = c / 2
Find Leg B
Leg b is the second-longest side opposite the 60° angle. Given the length of leg a or the hypotenuse c, the formulas to solve the length of leg b are:
b = a√3
b = c × √3 / 2
Find the Hypotenuse
In a 30 60 90 special right triangle, the hypotenuse is the longest side opposite the right angle, and it is always equal to twice the length of the shortest leg. Thus, the formula to calculate the hypotenuse c is simply c = 2a.
Given the length of leg a or b, the formulas to solve c are:
c = 2a
c = 2b × √3 / 3
Find the Area
Given the side lengths of a 30 60 90 triangle, you can find the area using the formula:
A = ab / 2
The area A is equal to leg a times leg b, divided by 2.
Find Perimeter
Like any triangle, the perimeter is equal to the sum of the side lengths.
P = a + b + c
So, perimeter P is simply leg a plus leg b plus hypotenuse c.
There is a special formula to find the perimeter of a 30 60 90 triangle if you know the length of leg a:
P = a × (√3 + 3)
The perimeter P is equal to the length of leg a times the quantity square root of 3 plus 3.
Like special right triangles? You might also like our 45 45 90 calculator.