Tangent Calculator – Calculate tan(x)
Find the tangent of an angle using the tan calculator below. Start by entering the angle in degrees or radians.
On this page:
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
Bailey is an experienced educator and specializes in K-12 math and science. She holds a Master's degree in professional education and holds several teaching certifications.
How to Find the Tangent of an Angle
In a right triangle, the tangent of angle α, or tan(α), is the ratio between the opposite side of an angle and the adjacent side.
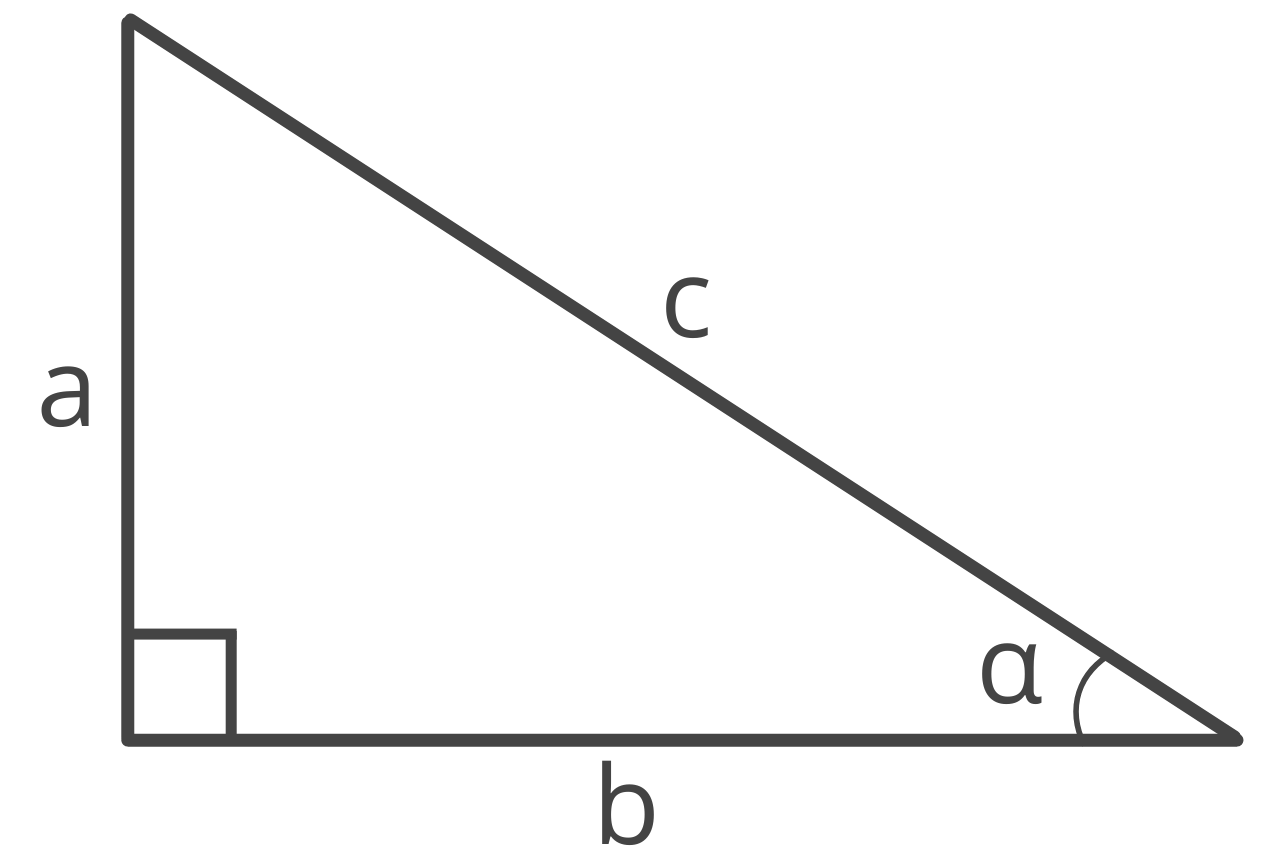
Tangent is one of the three primary trigonometric functions and is abbreviated tan.
You might be curious how to find the tangent of an angle. Use the formula below to calculate tan.
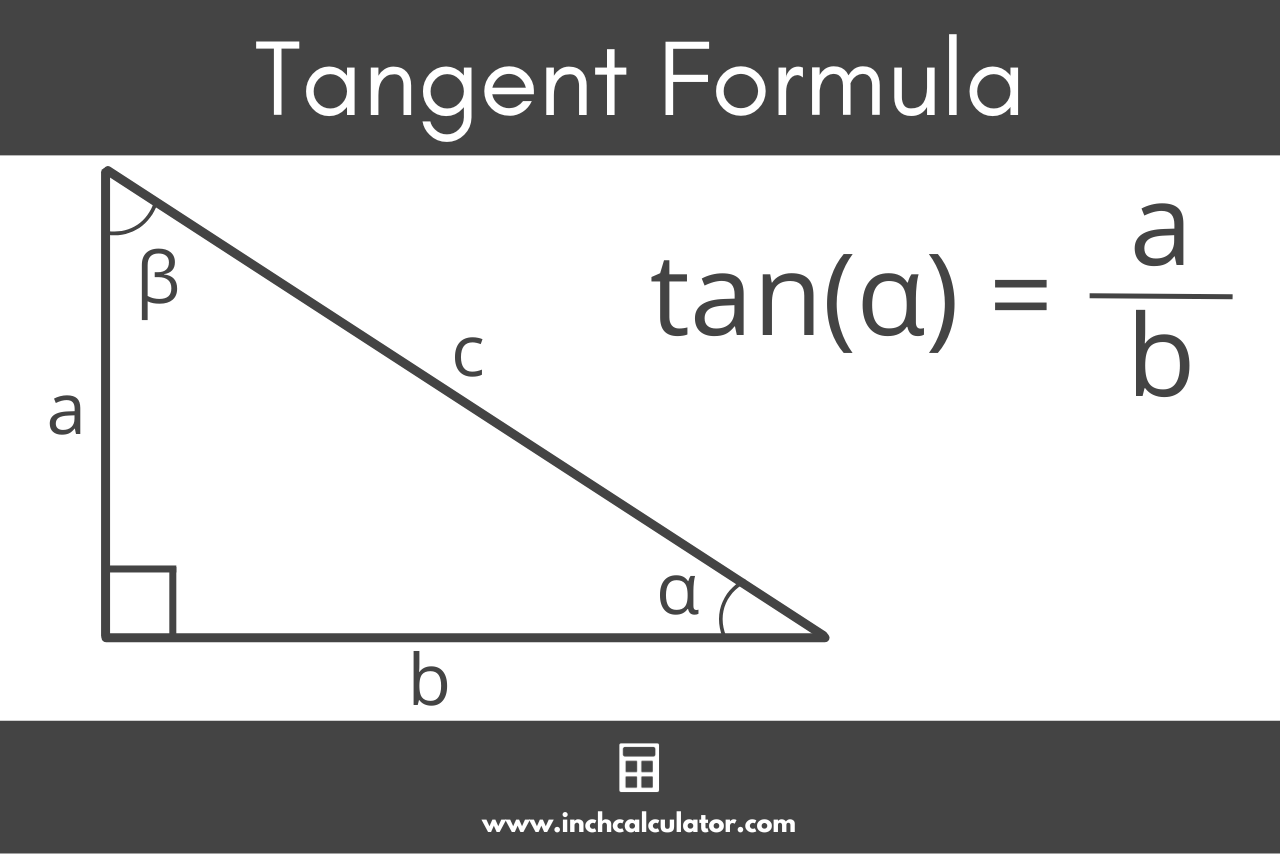
Tangent Formula
The tangent formula is:
tan(α) = opposite / adjacent = a / b
Thus, the tangent of angle α in a right triangle is equal to the opposite side’s length divided by the adjacent side’s length.
To find the ratio of tangent, simply enter the length of the opposite and adjacent and simplify.
For example, let’s calculate the tangent of angle α in a triangle with the length of the opposite side equal to 4 and the adjacent side equal to 8.
tan(α) = 4 / 8
tan(α) = 1 / 2
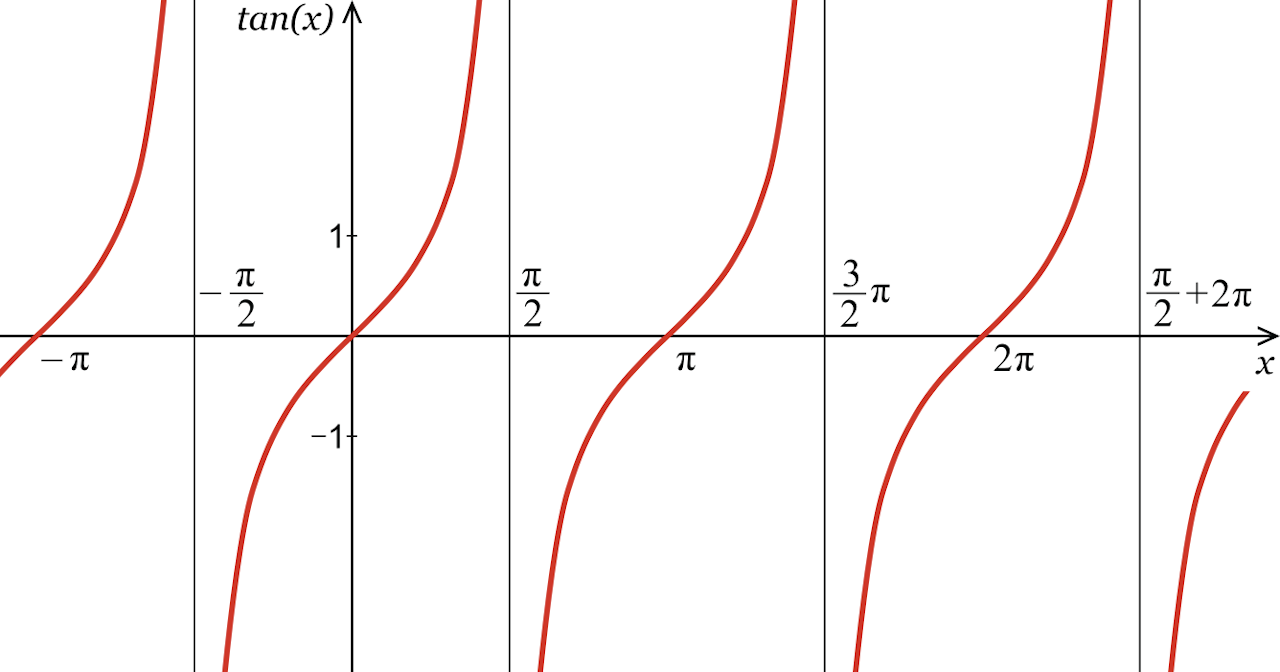
Tangent Graph
If you graph the tangent function for every possible angle, it forms multiple increasing curves with an asymptote at π/2 and repeating every π radians, or 180°. See values in the table below.
Tangent Table
The table below shows common angles and the tan value for each of them.
| Angle (degrees) | Angle (radians) | Tangent |
|---|---|---|
| 0° | 0 | 0 |
| 30° | π / 6 | 1 / √3 = √3 / 3 |
| 45° | π / 4 | 1 |
| 60° | π / 3 | √3 |
| 90° | π / 2 | undefined |
| 120° | 2π / 3 | -√3 |
| 135° | 3π / 4 | -1 |
| 150° | 5π / 6 | –1 / √3 = –√3 / 3 |
| 180° | π | 0 |
| 210° | 7π / 6 | 1 / √3 = √3 / 3 |
| 225° | 5π / 4 | 1 |
| 240° | 4π / 3 | √3 |
| 270° | 3π / 2 | undefined |
| 300° | 5π / 3 | -√3 |
| 315° | 7π / 4 | -1 |
| 330° | 11π / 6 | –1 / √3 = –√3 / 3 |
| 360° | 2π | 0 |
Inverse Tangent
The inverse of the tangent function is the arctan function. Thus, if you know the tan of an angle, you can use arctan to find the measurement of the angle.
Arctan can also be expressed as tan-1(x).
Cotangent
Cotangent, on the other hand, is a separate trigonometric function that is the reciprocal of the tangent value. The following formulas show the relationship between tangent and cotangent.
tan(α) = opposite / adjacent = a / b
cot(α) = adjacent / opposite = b / a = 1 / tan(α)
Note that the cotangent is not the same as arctan.
You might also be interested in our sine and cosine calculators.
Law of Tangents
The law of Tangents is a fundamental principle in trigonometry that relates the tangent of two angles and the sides of a triangle. It states that the ratio of the difference between the lengths of two sides to the tangent of the difference between the corresponding angles in a triangle is equal to the ratio of the sum of the lengths of the sides to the tangent of the sum of the corresponding angles.
You can use the law of tangents in trigonometry to find the lengths of sides or angles of a triangle when only given some information.
Frequently Asked Questions
Do you use degrees or radians with a tangent?
You can use both degrees and radians with tangents, but it is important to know which one you are using since each produces different results. Radians are more commonly used in trigonometry, therefore, to use degrees, you must convert them to radians using the formula:
radians = (degrees × π) / 180
You can also use our degrees to radians calculator to for this conversion. When working with the law of tangents, it’s important to use the same unit of angle measurement consistently.
Can you find a tangent without a calculator?
To find the tangent of an angle without a calculator, you can draw a right triangle and label the sides as opposite, adjacent, and hypotenuse.
Then, use the Pythagorean theorem to find the length of the hypotenuse and use the definition of the tangent function to find the tangent of the given angle by dividing the length of the opposite side by the length of the adjacent side.
Finally, simplify the expression for the tangent, if necessary.
How do you convert tangent to an angle?
To convert a tangent value to an angle, use the inverse tangent function, also known as arctan or tan-1. This function takes the tangent value as input and returns the angle in radians. To convert to degrees, multiply the angle in radians by 180/π, use the degree mode on your calculator, or use our radians to degrees calculator.
Does tangent repeat?
The tangent function repeats after certain intervals due to the fact that it is periodic. The period of the tangent function is π, or approximately 3.14159. Therefore, the tangent function has the same values for every x + kπ, where k is an integer.