Inverse Tangent Calculator – Calculate arctan(x)
Find the angle in degrees or radians using the inverse tangent with the arctan calculator below.
On this page:
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
Bailey is an experienced educator and specializes in K-12 math and science. She holds a Master's degree in professional education and holds several teaching certifications.
How to Find Arctan
Arctan is a trigonometric function to calculate the inverse tangent. Arctan can also be expressed as tan-1(x).
Arctan is used to undo or reverse the tangent function. If you know the tangent of an angle, you can use arctan to calculate the measurement of an angle.
Since arctan is the inverse of the tangent function, and many angles share the same tangent value, arctan is a periodic function. Each arctan value can result in multiple angle values, which is why the range is restricted to [-π/2, π/2].
To calculate arctan, use a scientific calculator and the atan or tan-1 function, or just use the calculator above. Most scientific calculators require the angle value in radians to solve for tan.
Inverse Tangent Formula
The inverse tangent formula is:
y = tan(x) | x = arctan(y)
Thus, if y is equal to the tangent of x, then x is equal to the arctan of y.
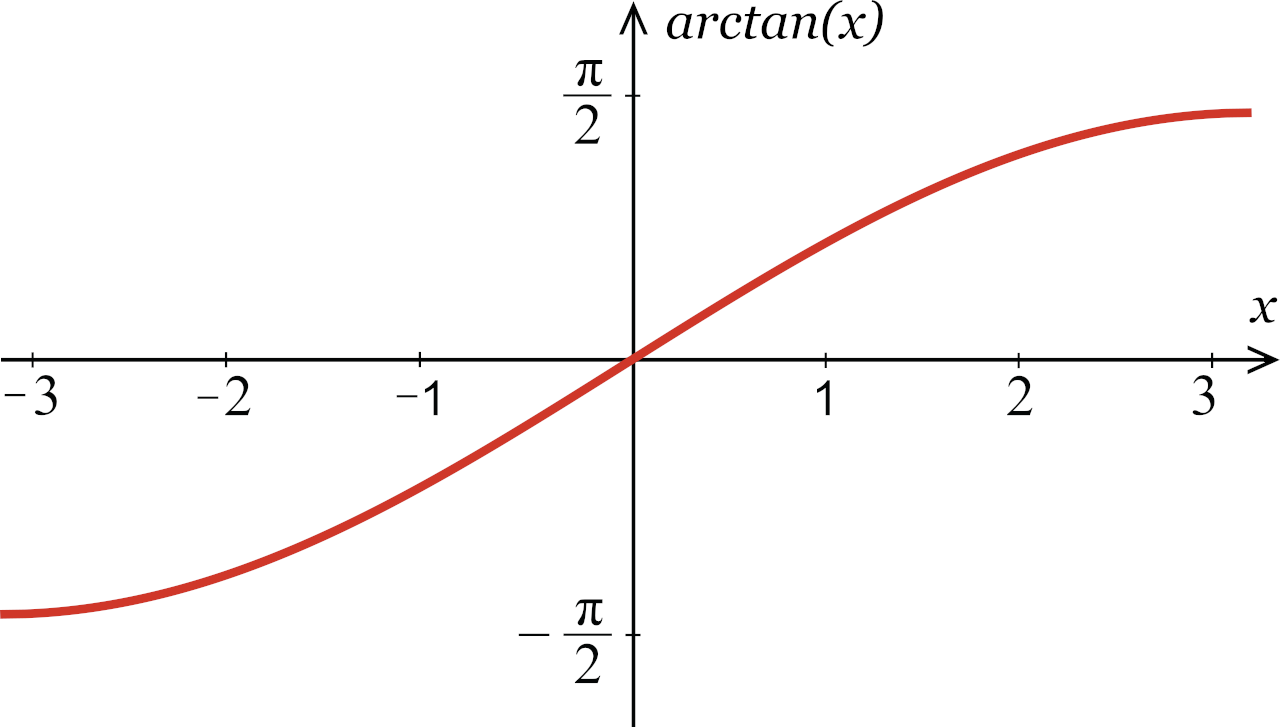
Inverse Tangent Graph
If you graph the arctan function for every possible value of tangent, it forms an increasing curve over all real numbers from (-∞, –π / 2) to (∞, π / 2). Horizontal asymptotes occur at y = –π/2 and y = π/2, which coincide with the values of the vertical asymptotes of the tangent function.
Inverse Tangent Table
The table below shows common tangent values and the arctan, or angle for each of them.
| Tangent | Angle (degrees) | Angle (radians) |
|---|---|---|
| -∞ | -90° | –π / 2 |
| -√3 | -60° | –π / 3 |
| -1 | -45° | –π / 4 |
| –√3 / 3 | -30° | –π / 6 |
| 0 | 0° | 0 |
| √3 / 3 | 30° | π / 6 |
| 1 | 45° | π / 4 |
| √3 | 60° | π / 3 |
| ∞ | 90° | π / 2 |
You might also be interested in our inverse sine and inverse cosine calculators.
How to use inverse tangent to find an angle in a right triangle
You can find the angle in a right triangle by finding the arctangent.
Begin by identifying and labeling the hypotenuse, opposite side, and adjacent side in regards to the angle you want to find.
Use the equation y = arctan(opposite/adjacent) and evaluate to find the angle in radians.
If the opposite and adjacent sides are known, you can find the value of y directly and round the answer to the nearest degree or decimal place.
If the opposite side and adjacent are not known, you can use the Pythagorean theorem to find the missing side lengths before using the above formula.
How to convert an inverse tangent to an inverse sine
To convert an inverse tangent (tan-1) to an inverse sine (sin-1), use the identity tan-1(x) = sin-1(x/√(1+x2)). We can understand this formula by looking at a right triangle with an angle theta and the opposite side x and adjacent side 1.
By using the Pythagorean theorem, we can solve for the hypotenuse as √(1+x2). Then, we can use the definition of the inverse sine function to find the angle whose sine is x/√(1+x2), which is equal to the inverse tangent of x.
Frequently Asked Questions
What is tangent to the power of -1?
Tangent-1 refers to the inverse tangent function or arctangent. This function takes a value between negative infinity and positive infinity as the input and returns an angle in radians as the output.
For example, if tangent(x) = -1, then tangent-1(-1) = -0.785 radians. This is approximately -45 degrees, which means that the angle whose tangent is -1 is -45 degrees or -0.785 radians.
Can you find the inverse tangent without a calculator?
Yes, you can find the inverse tangent, or arctangent, without a calculator by identifying the value that you want to find the inverse tangent for. Then write down the equation tan(y) = x and solve for y by taking the arctangent of both sides of the equation.
You can then evaluate the expression using algebraic methods for simple fractions or geometric methods for more complex values. Some values, however, may require you to use the table of trigonometric values.
For example, if you want to find the arctangent of 1, you can write tan(y) = 1 and solve for y to get y = π/4 or 45 degrees.
Can you find the inverse tangent for an angle in degrees?
Yes, once you find arctangent for an angle in radians, you can convert the value to degrees with the formula degrees = radians × (180 / π). You can also use our radians to degrees converter to get the angle in degrees.
Is the inverse tangent the same as 1 over tangent?
Although this is a common mistake, inverse tangent is not the same as 1/arctangent. Arctangent is the inverse of the cotangent function where 1/cotangent is the reciprocal of the tangent.