Rectangle Calculator
Use our rectangle calculator to find the area, perimeter, and diagonals of your shape.
Enter any two properties of a rectaingle to calculate the remaining properties.
Solution:
| Length (l): | 3
|
| Width (w): | 4
|
| Area (A): | 12
|
| Perimeter (P): | 14
|
| Diagonal (d): | 5
|
| Circumradius (R): | 2.5
|
| Inradius (r): | 1.5
|
On this page:
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
Pateakia has worked in education for 15 years and has three degrees, including a PhD, Master's degree, and Bachelor's degree. She specializes in mathematics.
How to Calculate the Properties of a Rectangle
A rectangle is a four-sided polygon (quadrilateral) with opposite sides that are equal in length and four right angles. Due to its symmetry, a rectangle has properties that distinguish it from other quadrilaterals, such as the parallelogram or the trapezoid.
A rectangle is defined by the length of its length and width, but also has other properties such as its area, perimeter, length of its diagonal bisection, circumradius, and inradius.
How to Calculate the Area of a Rectangle
The area of a rectangle is given by the product of its length and width. Thus, the formula to calculate a rectangle area is:
The area A is equal to the length l multiplied by the width w.
How to Calculate the Perimeter of a Rectangle
The perimeter of a rectangle is the sum of all its sides. Given its symmetrical nature, the perimeter can be expressed as:
The perimeter P is equal to twice the length l plus twice the width w.
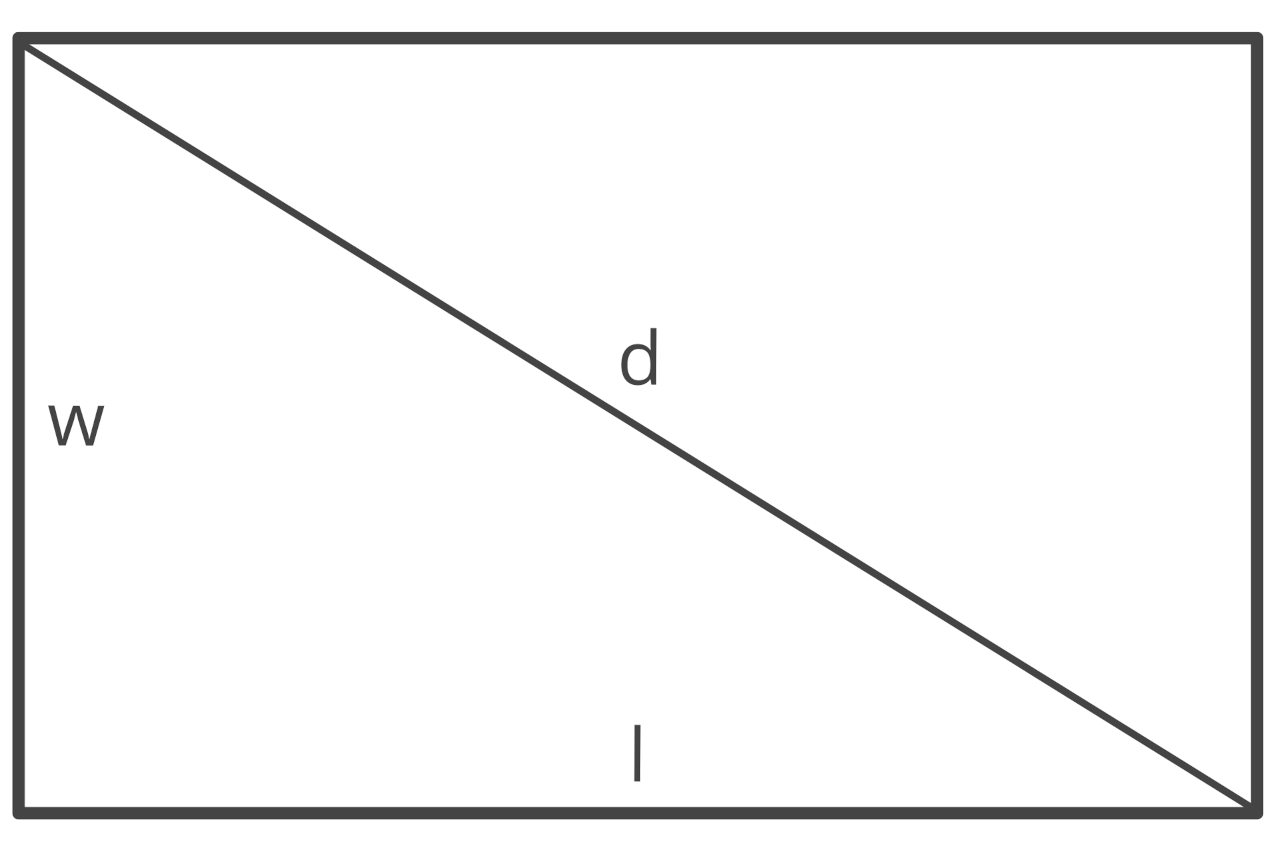
How to Calculate the Diagonals of a Rectangle
When you draw a diagonal across a rectangle, you effectively divide the rectangle into two congruent right triangles. The diagonal forms the hypotenuse of these triangles, and the rectangle’s length and width form the remaining two sides of the triangle.
Because the diagonal forms a right triangle, you can use the Pythagorean theorem to calculate the length of the diagonal. The Pythagorean theorem states:
The formula to calculate the length of a diagonal that bisects a rectangle is:
This can be simplified to:
The diagonal d of a rectangle is equal to the square root of the length l squared plus the width w squared.
How to Calculate the Circumradius and Inradius
The circumradius R of a rectangle is the radius of the circle that circumscribes the rectangle, passing through all its vertices. Given the symmetry of the rectangle, this is equivalent to half the length of its diagonal.
The inradius r of a rectangle is the radius of the inscribed circle that touches all four sides of the rectangle. It is equal to half the shorter side of the rectangle (or the width, if we assume the width is the shorter side):
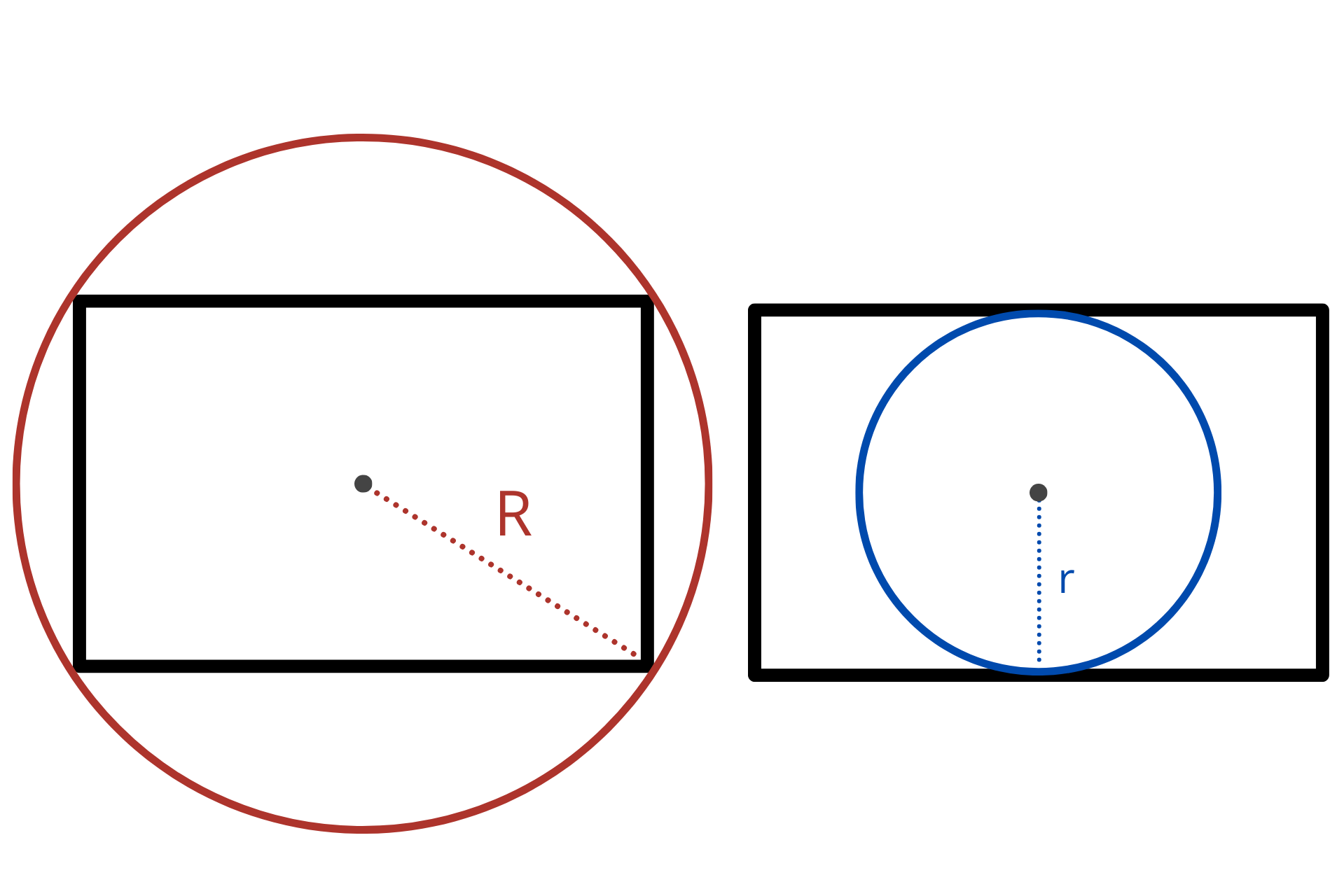
The formulas to calculate the circumradius and inradius are:
Practical Application of Rectangles
Understanding the properties of a rectangle is practical in many scenarios, including:
- Flooring and Tiling: To determine how many tiles you need for a room or how much carpet is required.
- Painting: To figure out how much paint will cover a rectangular wall.
- Building and Construction: For builders to figure out the square footage of a building or how much concrete is needed for a pad or footing.
- Agriculture and Landscaping: For farmers and landscapers to figure out the acreage of a rectangular plot of land and, subsequently, how many crops can be planted or how much sod/grass is needed.
- Design: For architects, artists, and designers to know the space they have to work within.