Slope Calculator
Use the slope calculator to find the slope of a line that passes through 2 points or solve a coordinate given m. Plus, the calculator will also solve the slope-intercept form of a line.
Find the Slope of a Line
Find Points on a Line at a Distance From Another Point
Find a Point on a Line Given it's x or y Value
Slope:
Line Graph:
Slope Intercept Form:
Point Slope Form:
Standard Form:
Angle, Distance, & Intercepts:
| Angle (θ): | 63.435°
|
|---|---|
| Distance: | 2.236
|
| Δx: | 1
|
| Δy: | 2
|
| x-Intercept: | -0.5
|
| y-Intercept: | 1
|
Steps to Find Slope
Start with the slope formula
Step One: Substitute point values in the formula
Step Two: Simplify the fraction
Step Three: Solve for slope (m)
| Right: | (x2, y2)
|
|---|---|
| Left: | (x2, y2)
|
Line Graph:
Slope Intercept Form:
Point Slope Form:
Standard Form:
Slope, Angle, and Intercepts:
| Slope (m): | |
|---|---|
| Angle (θ): | |
| x-Intercept: | |
| y-Intercept: |
Steps to Find Coordinates at a Distance From a Point
Step One: Solve for the right x2:
Step Two: Solve for the right y2:
Step Three: Solve for the left x2:
Step Four: Solve for the left y2:
Line Graph:
Slope Intercept Form:
Point Slope Form:
Standard Form:
Angle, Distance, & Intercepts:
| x2: | |
|---|---|
| y2: | |
| Slope (m): | |
| Angle (θ): | |
| Distance: | |
| Δx: | |
| Δy: | |
| x-Intercept: | |
| y-Intercept: |
Steps to Find the Missing Coordinate
Start with the slope formula
Step One: Substitute point values in the formula:
Step Two: Simplify the equation:
Step Three: Cross-multiply the fraction and solve:
On this page:
- Slope Calculator
- How to Find the Slope of a Line
- Slope Formula
- Steps to Find Slope Using the Formula
- How to Interpret Slope
- How to Find the Equation of a Line Using the Slope
- How to Find Slope-Intercept Form
- How to Find Point-Slope Form
- How to Find Standard Form
- How to Find the x and y Intercepts of a Line
- How to Find a Point Given 1 Point, Slope, and Distance
- How to Find the Distance Between 2 Points
- Frequently Asked Questions
- References
How to Find the Slope of a Line
Slope is a measure of the rate of incline or steepness of a line on a graph. You can find the slope of a line by comparing any 2 points on the line. A point is an x and y value of a cartesian coordinate on a grid.
Slope, expressed as m, is equal to the rise between two coordinates on a line over the run, or rather, it’s the ratio of rise to run.
Rise is the vertical change of the line, or the change in altitude or elevation, and the run is the horizontal change, or the change in distance.[1] In mathematical terms, on a cartesian coordinate grid, rise is the change in y and run is the change in x.
Slope Formula
You can find the slope m of a line using the following formula:[2]
m = y2 – y1 / x2 – x1
Thus, the slope m is equal to y2 minus y1, divided by x2 minus x1. This is often referred to as the rise over run formula.

Steps to Find Slope Using the Formula
To find the slope of a line using this formula, you’ll need to take any two points along a line and use their x and y values. The value of x is the horizontal distance of the point from the vertical y-axis, and y is the vertical distance of the point from the horizontal x-axis.
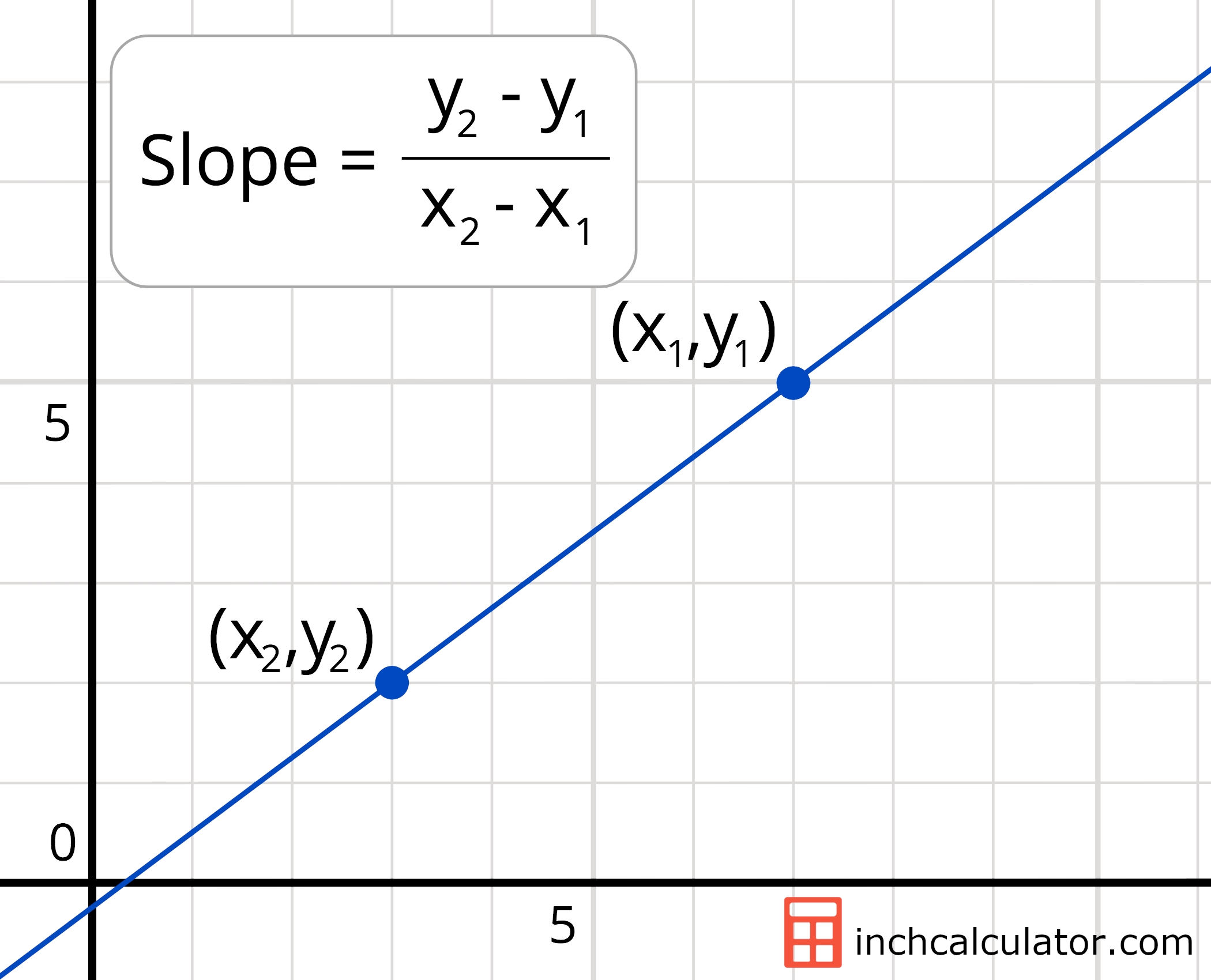
Then, follow three easy steps to calculate the slope.
Step One: Substitute Points in the Slope Formula
Start by replacing the y1, y2, x1, and x2 values in the formula with the coordinates for the two points on the line.
Step Two: Find the Difference in x and y Coordinates
Next, evaluate the numerator and denominator of the slope formula using these values. The absolute value of the numerator will be the vertical distance between the two points, and the absolute value of the denominator will be the horizontal distance between the two points.
The numerator represents the change in the value of y, which is known as the delta of y, or just Δy. You can find the delta of y using the formula:
Δy = y2 – y1
The denominator represents the change in the value of x, which is known as the delta of x, or Δx. You can find the delta of x using the formula:
Δx = x2 – x1
Step Three: Divide the Delta of y by the Delta of x
The final step is to divide the delta of y by the delta of x to find the slope. You can do this by dividing the numerator in the slope formula by the denominator, or more simply, by using a fraction to decimal calculator.
In some cases, you may want to represent the slope as a fraction or ratio. In this case, you can simplify the fraction to reduce it to its simplest form rather than converting it to a decimal.
For example, let’s find the slope of a line that passes through points (3,2) and (11,8).
Start with the slope formula:
m = (y2 – y1) / (x2 – x1)
Replace the x and y values with the x and y coordinates values.
m = 8 – 2 / 11 – 3
Evaluate the numerator and denominator to find the delta of x and y.
m = 8 – 2 / 11 – 3 = 6 / 8
Then, reduce the fraction to its simplest form.
m = 6 / 8 = 3 / 4
So, the slope m is equal to 3 / 4
The slope formula is useful for points along a line, but when working with non-linear functions, you might need to use an average rate of change calculator.
How to Interpret Slope
While the slope of a line doesn’t tell us where the line is located on the graph, it does tell us the angle of the line.
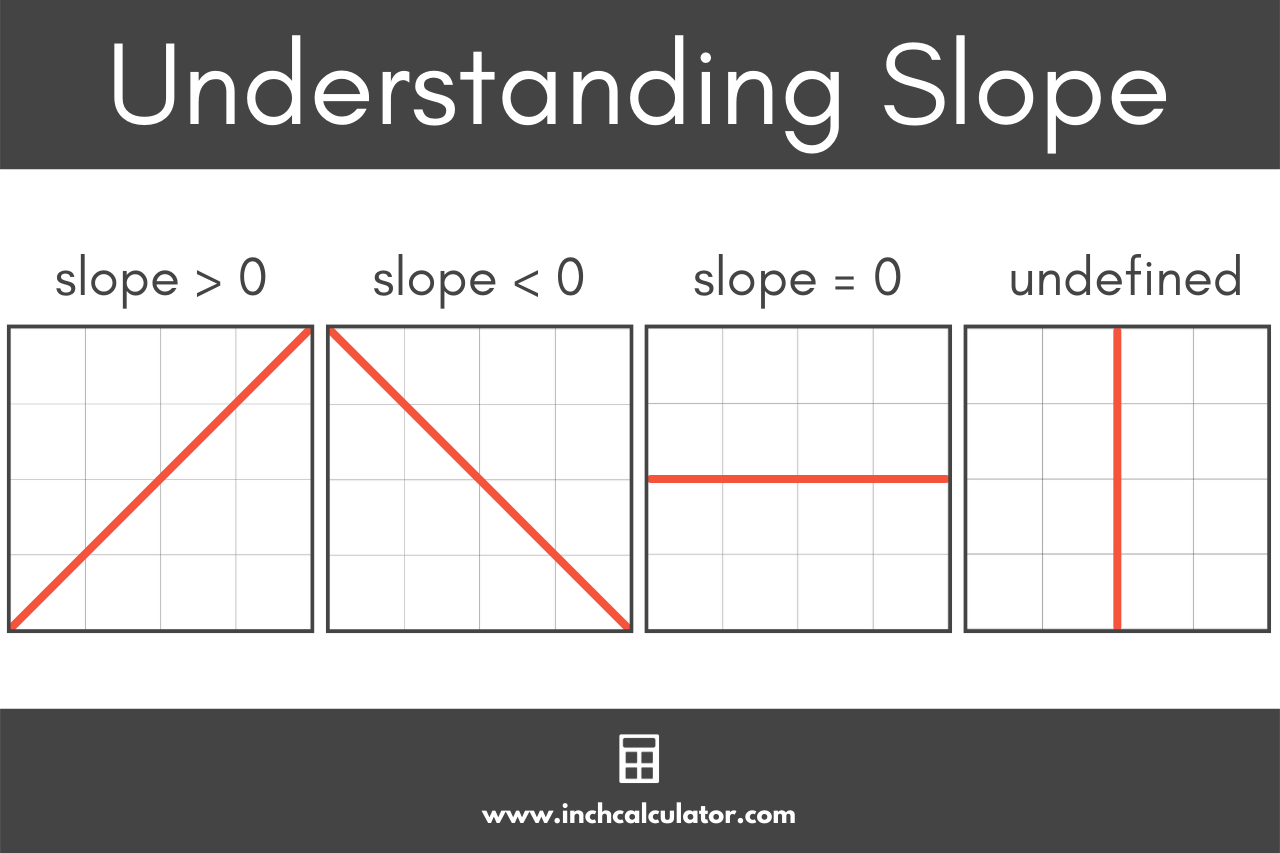
If the slope is positive, then the line is slanted up and rises from left to right on the graph.
If the slope is negative, then the line is slanted down and drops from left to right on the graph.
If the slope is equal to zero, the line is horizontal and does not slant up or down. This is known as a line with no slope.
In the special case of a vertical line, the slope is undefined. This is because any two points on the line have the same x value, so delta x would equal zero. Therefore, when calculating the slope, one would be dividing by zero, thereby making the slope infinite or undefined.
How to Find the Equation of a Line Using the Slope
Now that you found the slope, you can mathematically express a linear line using one of several equations. The most common equations for a line are slope-intercept form, point-slope form, and standard form.
How to Find Slope-Intercept Form
Slope-intercept form is one of the most commonly used equations to represent a line. You can find the equation of a line using slope-intercept form given the slope m and one point on the line.
Slope-Intercept Form Equation
The slope-intercept form equation is:[3]
y = mx + b
The slope-intercept form equation states that the y value of a coordinate on the line is equal to the x value of the coordinate times the slope m, plus the y-intercept b.
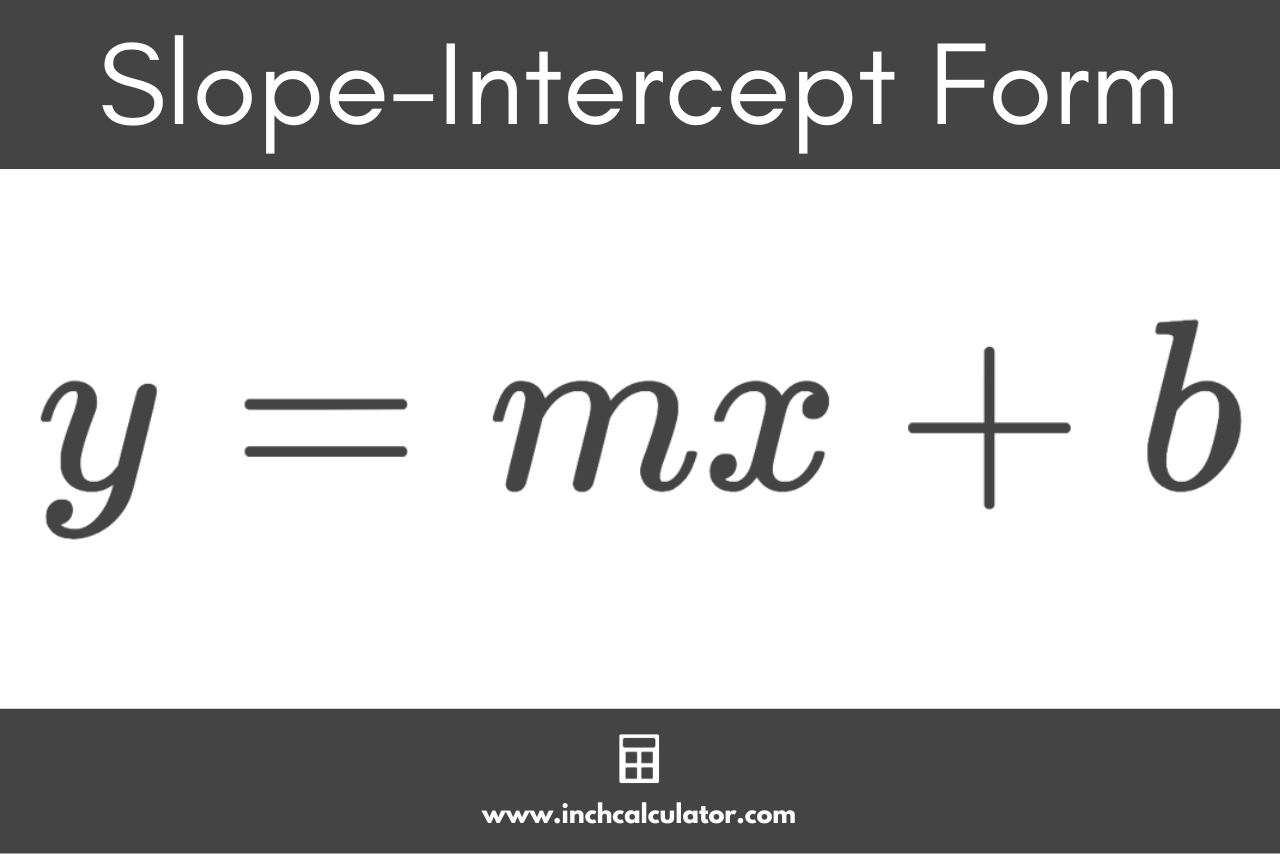
For example, let’s solve for b, given a slope of 1/2 and a point (5,4). We’ll express the equation for this line in slope-intercept form.
Substitute for m:
y = 1/2x + b
Substitute the point values for x and y:
4 = 1/2 × 5 + b
Solve for b:
4 = 2.5 + b
4 – 2.5 = b
1.5 = 3/2 = b
Substitute b in the equation to find the slope-intercept form:
y = 1/2x + 3/2
How to Find Point-Slope Form
Point-slope form is another commonly used equation to represent a line. You can find the equation of a line using point-slope form given the slope m and one point on the line.
Point-Slope Form Equation
The point-slope form equation is:[4]
y – y1 = m(x – x1)
The point-slope form equation states that y minus the y1 coordinate is equal to the slope m times x minus the x1 coordinate.
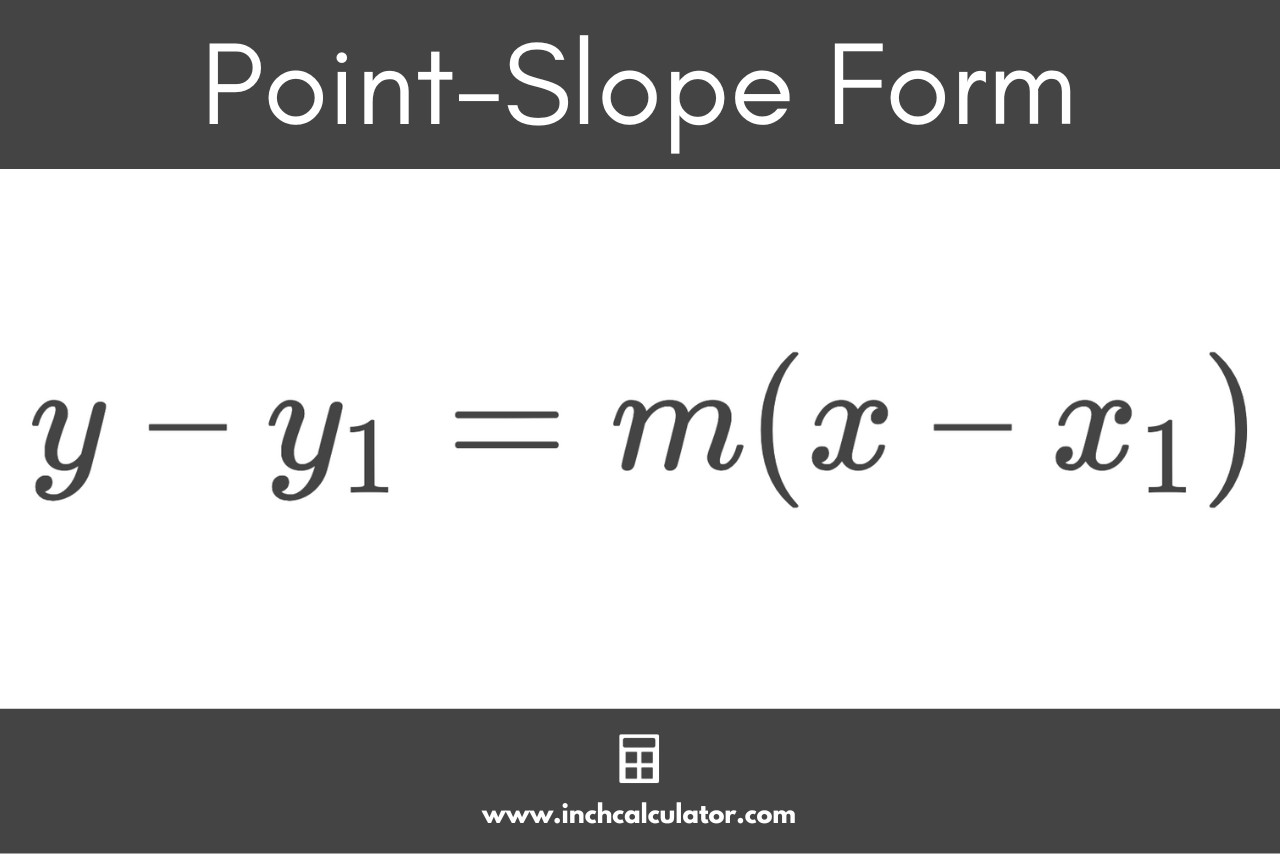
For example, let’s express the same line from the previous example using point-slope form. Recall the line has a slope of 1/2 and a point (5,4).
Substitute for m:
y – y1 = 1 / 2(x – x1)
Substitute the point values for x and y:
y – 4 = 1 / 2(x – 5)
So, the point-slope form for this line is y – 4 = 1 / 2(x – 5).
How to Find Standard Form
Standard form is a standardized format for linear equations. To use standard form, the slope and coordinates should be whole numbers; decimal values are generally not used in standard form.
Standard Form Equation
The standard form equation is:
Ax + By = C
Given either of the linear equations above, you can convert to standard form by simply rearranging the equations to isolate the constant C on one half of the equation. If there are any fractions, then multiply both sides of the equation by the denominator of the fractions to remove them.

This formula represents the standard form for linear equations. (Numbers can also be expressed in standard form as well!)
How to Find the x and y Intercepts of a Line
Given the slope of a line and one point on it, you can find the x and y intercepts using one of the linear equations above. The x-intercept is where the line crosses the x-axis, and the y-intercept is where the line crosses the y-axis.
To find these values, start by finding the equation’s slope-intercept form.
Then, given slope-intercept form, you can find the y-intercept by setting x in the equation to 0 and solving for y.
Similarly, to find the x-intercept, set y in the equation to 0 and solve for x.
For example, let’s find the x and y intercepts of the line y = 1/2x + 8.
To find the y-intercept, start by setting x to 0.
y = (1/2 × 0) + 8
Then solve for y.
y = 8
When x is equal to zero, y is equal to 8, so 8 is the y-intercept.
Next, to find the x-intercept, set y equal to 0.
0 = 1 / 2x + 8
Then solve for x.
0 = 1/2x + 8
0 – 8 = 1/2x + 8 – 8
-8 = 1/2x
-8 × 2 = 1/2x × 2
-16 = x
When y is equal to zero, x is equal to -16, so the x-intercept is -16.
How to Find a Point Given 1 Point, Slope, and Distance
Points on a line can be found given the slope of the line m and the distance from another point d. Say we have point 1 with the coordinates (x1, y1), and we’re trying to find the coordinates (x2, y2) of point 2.
The formulas to find x2 and y2 if point 2 is to the right of point 1 are:
x2 = x1 + d / (1 + m2)
y2 = y1 + m × d / (1 + m2)
The formulas to find x2 and y2 if point 2 is to the left of point 1 are:
x2 = x1 – d / (1 + m2)
y2 = y1 – m × d / (1 + m2)
How to Find the Distance Between 2 Points
The formula to find the distance d between two points on a line is:
d = √((x2 – x1)2 + (y2 – y1)2)
You might also be interested in finding the midpoint or endpoints of a line using one of our calculators.
Frequently Asked Questions
How is finding slope used in real life?
Slope is commonly used in various different jobs. Some real-world applications of finding slope are calculating roof pitch, grade for roadwork or landscaping, ramps for wheelchairs, steps & stairs, and designing vehicles to be more aerodynamic.
Whenever we want to find the steepness or incline of a line, we ultimately need to find its slope.
How do you calculate percent slope?
Percent slope, sometimes referred to as grade, is a representation of the slope in percent form. You can calculate percent slope by dividing the vertical change by the horizontal change (or rise/run), then converting the result to a percentage.
percent slope = rise / run × 100%
For example, if a hill has a rise of 200′ over a horizontal distance of 400′, then the grade is 50%.
200′ / 400′ × 100% = 50%
How do you convert an angle to slope?
It’s also possible to convert an angle (in degrees) to slope; one must simply take the tangent of the angle.
m = tan(θ)
For example, if the angle = 72 degrees, then m is equal to tan(72), which equals approximately 3.08.
How do you convert a slope to an angle?
The angle of a line in degrees can be found from the inverse tangent of the slope m:
θ = tan-1(m)
For example, if m = 5, then the angle in degrees is tan-1(5), which is approximately equal to 78.7 degrees.
Our rise and run to degrees converter can help calculate the value in degrees given the rise and run of a line.
How do you find the slope of a curve?
This is a bit trickier than finding the slope of a line and actually involves some calculus. If, however, you only want to find the average slope of a curve between two points on that curve, you can use the slope formula above.
Just plug in your coordinates (x1, y1) and (x2, y2) like the example above to calculate m, but remember, this is only the average slope between the two points, not the slope at every point on the curve.
References
- LibreTexts Mathematics, Your Guide to Intermediate Algebra - 3.3: Slope Intercept Form, https://math.libretexts.org/Courses/Kansas_State_University/Your_Guide_to_Intermediate_Algebra/03%3A_Linear_Equations_and_Graphs/3.03%3A_Slope_Intercept_Form
- Marecek, L., Mathis, A., Intermediate Algebra 2e - 3.2 Slope of a Line, OpenStax, https://openstax.org/books/intermediate-algebra-2e/pages/3-2-slope-of-a-line
- CK-12 Foundation, Linear Equations in Slope-Intercept Form, https://www.ck12.org/book/ck-12-algebra-basic/section/5.1/
- Clapham, C., Nicholson, J., Oxford Concise Dictionary of Mathematics, 475. https://web.archive.org/web/20131029203826/http://web.cortland.edu/matresearch/OxfordDictionaryMathematics.pdf


