Roof Pitch Calculator

Calculate roof pitch by entering the rise and run or the angle in degrees. Learn more about measuring roof pitch and the rise and run below.

Find Roof Pitch From:

Results:

Pitch

per Foot

Grade (slope)

Degrees

Radians

Learn how we calculated this below

scroll down

Add this calculator to your site

How to Calculate Roof Pitch

Homes and other buildings have roofs with slopes ranging from no slope or flat to very steep slopes. Roof pitch describes the slope, or angle, of the roof.

Knowing roof’s pitch is essential in determining the appropriate installation method and how much roofing material you’ll need. It’s also an important factor in cold climates for calculating snow load.

Roof pitch, or slope, is a measure of vertical rise to horizontal run expressed in inches per foot.^[1] A roof with a 6″ rise for every 12″ run has a 6″ per foot, or 6 in 12 pitch.

Thus, the pitch is the ratio of the rise in inches to a 12-inch run and is often expressed using a semicolon, for example, 6:12. Sometimes the pitch is also expressed in fraction form using a fraction with a slash, such as 6/12.

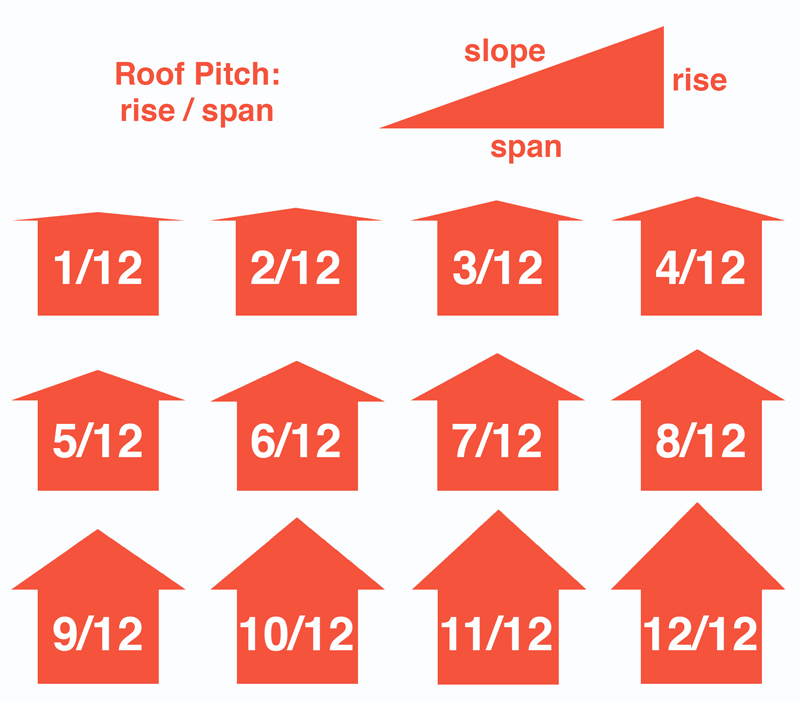
Chart showing standard roof pitches and illustrating that pitch is a measure of a roof's angle expressed as the rise over a 12-inch run.

You can measure roof pitch by finding the rise and run, or by converting from the angle if it is known. See the chart below for the rise and run values for standard roof pitches.

We’ll cover four methods to calculate roof pitch below.

Method One: Measure From the Roof

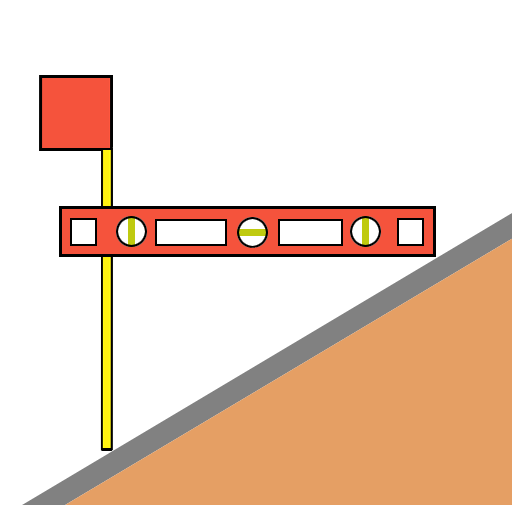
One method to find the pitch is to climb on the roof and measure the rise for a 12″ run. You’ll need a level that is 12″ or longer and a tape measure.

On the roof, hold the level perfectly level, and measure the height from the roof to the level 12 inches away from where the level touches the surface; this will be the rise.

For example, if the end of a level is 4″ above the roof at a point 12″ away from where it meets the surface, then the pitch is 4:12.

Graphic showing how to find the roof pitch using a level and tape measure by measuring the rise over run

Method Two: Measure From the Attic

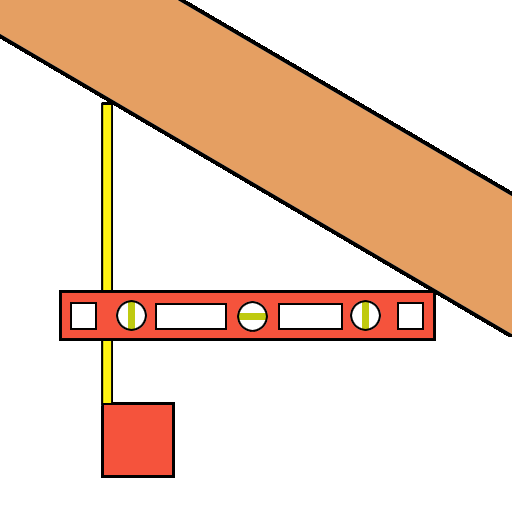
Another method to find the roof pitch is to go into the attic and measure the rise over a 12″ run of the roof rafters, allowing you to find the pitch without going on the roof.

From the attic, hold a level perfectly level and touching a rafter at one end. Measure the distance from the level to the rafter 12 inches away from where the level touches the rafter.^[2]

Graphic showing how to measure roof pitch from the attic using a level and tape measure

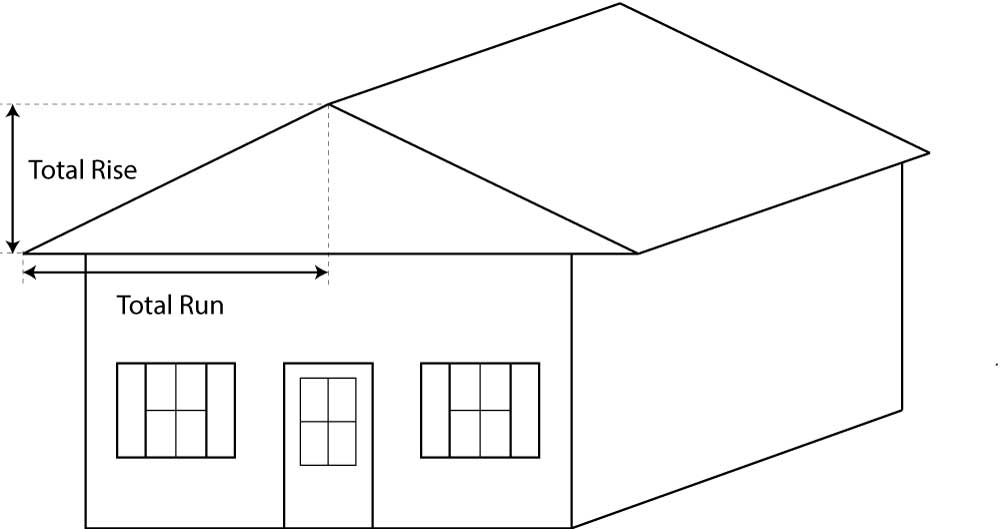
Method Three: Measure the Total Rise and Run

If you know the total height of the peak and the roof’s width, you can also find the pitch with a little math. For example, if the peak is 4 feet and the total roof width is 20 feet, then the total rise is 4 feet, or 48 inches.

The total run is the distance from the peak to the edge of the roof, which in this case is the total width divided in half, which is equal to 10 feet or 120 inches.

Illustration showing how to find roof pitch by measuring the total rise and total ru, then reducing to a rise over a 12 inch run.

Since the pitch is the rise over a 12-inch run, you can divide the run by 12 to get the multiplier, in this case, 120 ÷ 12 = 10.

Then, divide the rise by the multiplier to get the pitch, e.g. 48 ÷ 10 = 4.8. The pitch of this roof is 4.8:12. The calculator above can handle much of this math.

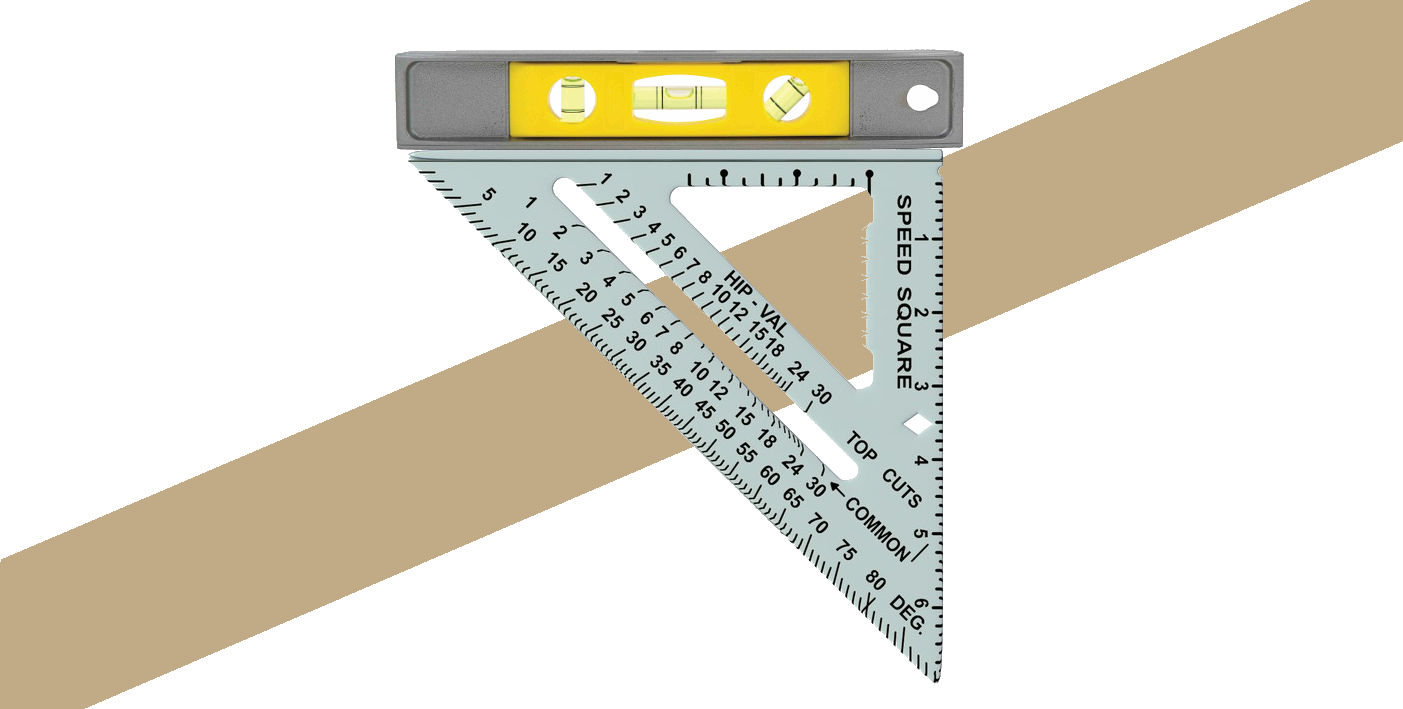
Method Four: Measure With a Speed Square

You can also use a speed square and level to quickly measure the roof’s pitch. Set the level on the edge of the speed square as shown below, then place the heel of the speed square on a rafter or gable edge of the roof.

Holding the level and speed square level, locate the measurement on the speed square where it meets the rafter’s bottom edge to find the angle of the roof in degrees.

Image showing how to measure roof pitch in degrees using a speed square and level

How to Convert Angle in Degrees to Roof Pitch

If you know the roof’s angle in degrees, you can find the roof pitch by converting the angle in degrees to a slope, then finding the rise by multiplying the slope by 12.

First, find the slope by finding the tangent of the degrees, e.g. slope = tan(degrees). Then multiply the slope by 12 to get the rise. You can then express the pitch as inches per foot.

Example: let’s find the pitch for a roof angle of 35°.

slope = tan(35°) = 0.7002
rise = 0.7002 × 12 = 8.4
pitch = 8.4:12

How to Convert Roof Pitch to Degrees

To find the angle of a roof in degrees, convert the pitch to a slope, then convert to degrees by finding the slope’s inverse tangent, or arctangent. First, convert the pitch to a slope.

To do this, simply convert the rise and run as a fraction to a decimal form, e.g. rise/run = rise ÷ run = slope. For a pitch expressed in inches per foot, convert to a fraction first, e.g. a 4 in 12 pitch becomes 4/12, then divide.

Next, find the degrees by finding the slope’s inverse tangent, e.g. degrees = arctan(slope).

For example: let’s find the angle in degrees for a roof with a 4 in 12 pitch.

slope = 4:12 = 4 / 12 = .333
angle = arctan(.333)
angle = 18.4178°

Learn more about finding the angle of a line using our slope calculator.

Standard Roof Pitches

Most roofs have a pitch in the 4:12 to 9:12 range. A pitch over 9:12 is considered a steep-slope roof, between 2:12 and 4:12 is a low-slope roof, and less than 2:12 is a flat roof.^[3]

The table below shows standard roof pitches and the equivalent grade and angle in degrees and radians for each.

Table showing standard roof pitches and the equivalent grade and angle in degrees and radians.
Pitch	Grade (slope)	Degrees	Radians
1/8:12	1%	0.6°	0.01
1/4:12	2.1%	1.2°	0.02
1/2:12	4.2%	2.4°	0.04
1:12	8.3%	4.8°	0.1
2:12	16.7%	9.5°	0.2
3:12	25%	14°	0.2
4:12	33.3%	18.4°	0.3
5:12	41.7%	22.6°	0.4
6:12	50%	26.6°	0.5
7:12	58.3%	30.3°	0.5
8:12	66.7%	33.7°	0.6
9:12	75%	36.9°	0.6
10:12	83.3%	39.8°	0.7
11:12	91.7%	42.5°	0.7
12:12	100%	45°	0.8
13:12	108.3%	47.3°	0.8
14:12	116.7%	49.4°	0.9
15:12	125%	51.3°	0.9
16:12	133.3%	53.1°	0.9
17:12	141.7%	54.8°	1
18:12	150%	56.3°	1
19:12	158.3%	57.7°	1
20:12	166.7%	59°	1
21:12	175%	60.3°	1.1
22:12	183.3%	61.4°	1.1
23:12	191.7%	62.4°	1.1
24:12	200%	63.4°	1.1

How Pitch Affects the Cost of Roofing

The pitch of a roof will have a definite impact on the cost to install or replace it. Steeper roofs cost more to install, so bear that in mind when choosing the right pitch for your project.

A low-slope roof might cost 10% more to install than a flat-roof, while a steep-slope roof might cost 20-30% more. Roofs with a very steep pitch might cost even more than that to install.

If you’re considering a new roof, we suggest getting several estimates to learn more about the right pitch for your roof and understand the cost of installation. We also cover more about roof replacement cost in detail in our cost guide.