Rise Over Run Calculator
Calculate the slope of a line or incline using rise over run, or calculate the rise and run given two points on a line.
Slope:
| Fraction: | |
|---|---|
| Decimal: | |
| Degrees: | |
| Percentage: |
| Rise: | |
|---|---|
| Run: | |
| Slope: |
On this page:
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
Bailey is an experienced educator and specializes in K-12 math and science. She holds a Master's degree in professional education and holds several teaching certifications.
What is Rise Over Run?
The slope of a line is expressed as a fraction with the rise over the run. The rise (expressed Δy) is the vertical change between points on the line, and the run (expressed Δx) is the horizontal change between points.
In other words, rise over run is how far up (Δy) and how far over (Δx) you go on a coordinate plane.
Rise Over Run Formula
Thus, the rise over run formula to find the slope of a line is:
slope = rise / run = Δy / Δx
The formula states that the slope of a line is equal to the rise (Δy) divided by the run (Δx).
How to Use Rise Over Run to Find Slope
You can find the slope of the line by dividing the rise by the run. To find the rise and run, start by finding two points along a line. We can call these points (x1, y1) and (x2, y2).
Calculate the rise by subtracting the y coordinate of one point from the other (y2 – y1). Calculate the run by subtracting the x coordinate of one point from the other (x2 – x1).
Then, substitute these values in the rise over run formula above to find the slope.
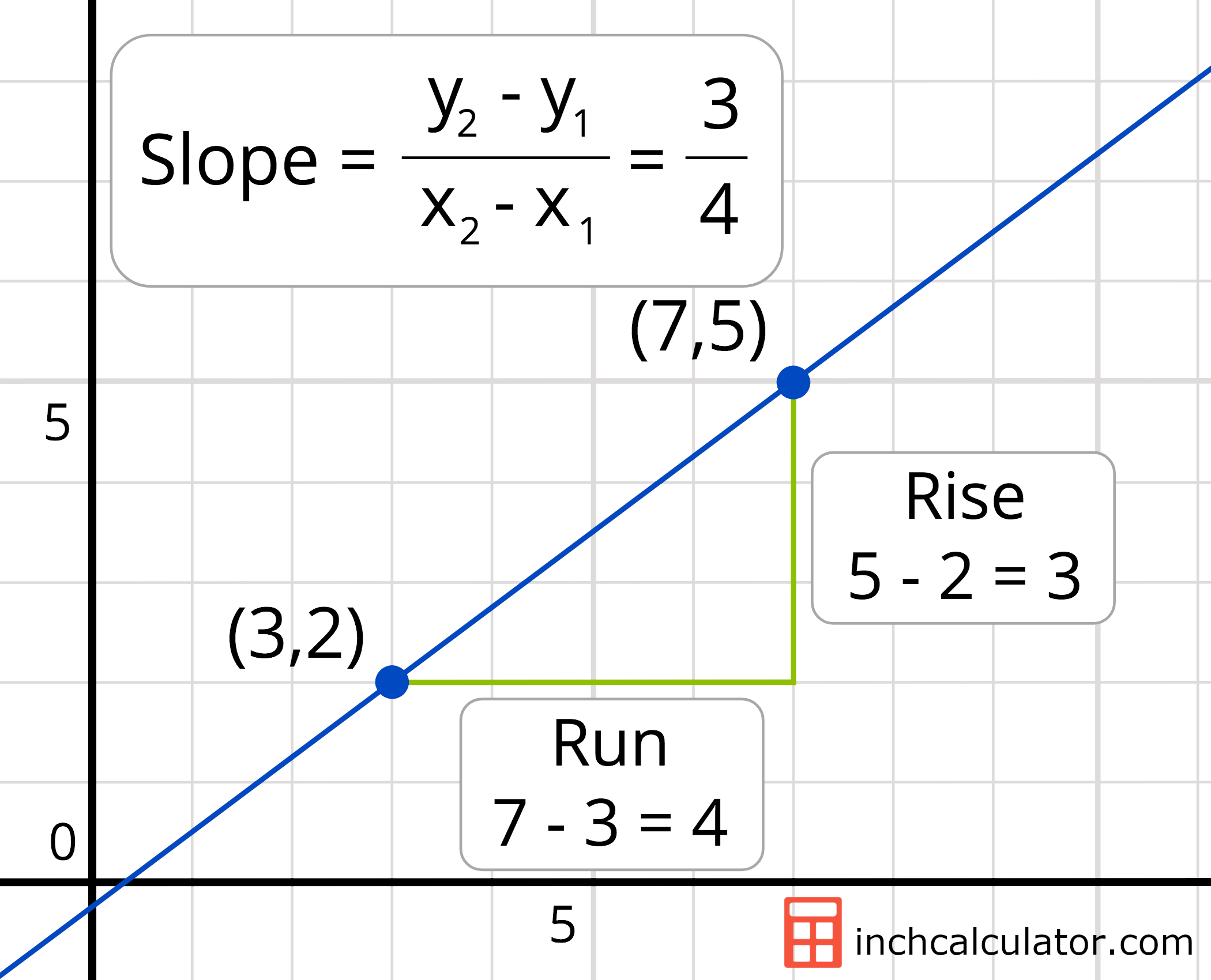
For example, let’s use rise over run to find the slope of a line that passes through points (3, 2) and (7, 5).
Start by finding the rise:
Δy = 5 – 2 = 3
Then find the run:
Δx = 7 – 3 = 4
Use the rise over run formula to find the slope:
slope = 3 / 4
So, the slope is equal to 3 / 4
Frequently Asked Questions
How is rise over run used in real life?
Some real-world examples of using rise over run to find slope are calculating roof pitch, grade for roadwork, wheelchair ramps, stairs & steps, and improving vehicle aerodynamics.
Rise and run are used whenever we need to measure an incline.
How do you find rise and run on a graph?
You can find the rise and run of a line on a graph by identifying two points on the graph, then calculating the difference between their y coordinates and the distance between their x coordinates.
The rise is the difference between the y coordinates, and the run is the distance between the x coordinates.
How do you convert rise and run to an angle?
You can find the angle of a line using the inverse tangent of the rise over the run.
θ = tan-1(rise/run)
The result θ is the angle in degrees.