Fraction to Decimal Calculator
Convert a fraction to a decimal by entering your fraction below. Keep reading to see four different ways to turn a fraction into a decimal without a calculator below.
Decimal Result:
Steps to Solve
Convert the fraction to a decimal by dividing the numerator by the denominator:
On this page:
- How to Convert a Fraction to Decimal
- Method 1: Convert a Fraction to Decimal Using a Calculator
- Method 2: Convert a Fraction to Decimal Using Long Division
- Method 3: Convert a Fraction to Decimal by Simplifying
- Method 4: Use a Conversion Chart
- Fraction to Decimal Conversion Chart
- How to Convert Mixed Fractions to Decimal
- Frequently Asked Questions
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
Bailey is an experienced educator and specializes in K-12 math and science. She holds a Master's degree in professional education and holds several teaching certifications.
How to Convert a Fraction to Decimal
A number can be expressed as a fraction, decimal, or percentage, and sometimes it’s necessary to convert between the different forms to represent a number differently.
There are several methods to convert a fraction to a decimal; we’ll cover each of them below.
Method 1: Convert a Fraction to Decimal Using a Calculator
The simplest method to transform a fraction number to a decimal value is to simply divide the numerator by the denominator to get the decimal value. The numerator is the top number, and the denominator is the bottom number.
So, the fraction to decimal formula is:
numerator / denominator = numerator ÷ denominator
For example, let’s convert the fraction 1/8 to a decimal using the division method. You can use a basic calculator to divide and find the result.
1 / 8 = 1 ÷ 8 = 0.125
Thus, the decimal value of 1/8 is 0.125
You might also be interested in our fraction to percent calculator for similar conversions.
Method 2: Convert a Fraction to Decimal Using Long Division
Long division offers another way to convert to decimal form. This is done by identifying the dividend and the divisor, then using those values in long division.
First, find the dividend and the divisor. The fraction’s numerator will be the dividend, and the denominator will be the divisor.
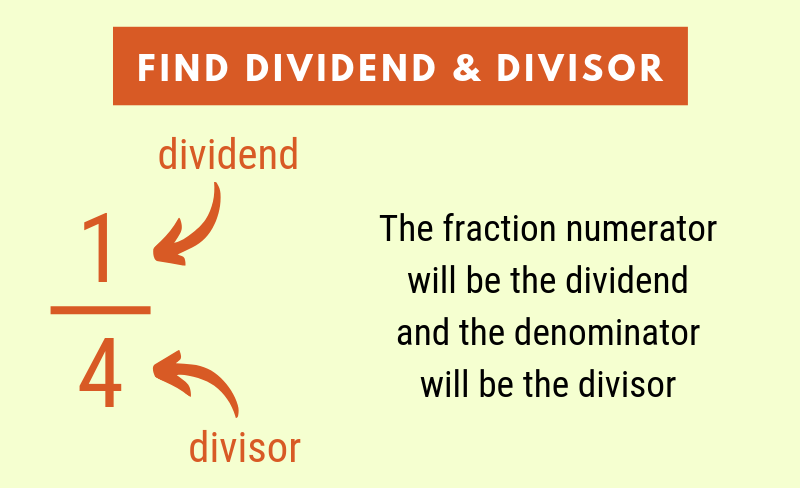
Next, place the dividend and divisor in long division form. You will need to add a decimal point and as many zeros as needed if the dividend is smaller than the divisor.
Finally, solve the long division problem to complete the conversion from fraction to decimal.
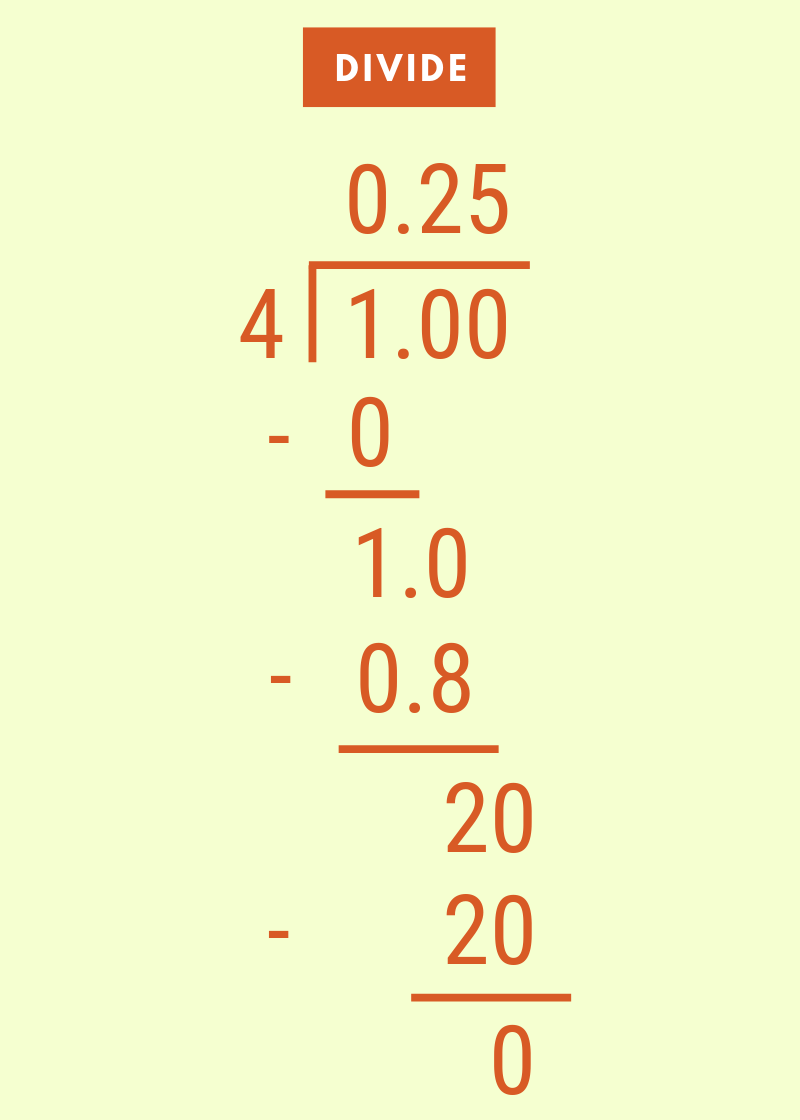
Here’s a tip: use a long division calculator to solve this problem and see each step.
Method 3: Convert a Fraction to Decimal by Simplifying
An alternate method to convert a fraction to a decimal number is to express the numerator as a fraction over 100.
When a fraction is out of 100, it is much easier to convert the value into a decimal because decimals are based on a system of powers of 10. This requires a few steps.
First, multiply the denominator to get to 100. To do this, you can divide 100 by the denominator to obtain the factor and then multiply both the numerator and denominator by that factor.
Next, you have to move the decimal point two places to the left for both the numerator and denominator to simplify the fraction. This will create a fraction out of 1. Since any fraction out of 1 is equal to the decimal value, the numerator is your final result.
For example, let’s convert the fraction 1/16 to a decimal value using this method.
Start by finding the multiple needed to multiply the denominator by to get 100.
100 = 16 × 6.25
That means that the multiple is 6.25.
Now, multiply the numerator by the multiple (6.25).
1 × 6.25 = 6.25
Thus, the fraction 1/16 can also be represented as 6.25/100.
1 / 16 = 6.25 / 100
Move the decimal place of the top and bottom left two places to simplify.
6.25 / 100 = 0.0625 / 1
The numerator is the resulting decimal.
0.0625 / 1 = 0.0625
So, the decimal value of 1/16 is 0.0625.
Method 4: Use a Conversion Chart
Another way to convert fractions to decimals is to consult a conversion chart, such as the one below, which shows the decimal values of a few common fractions.
Fraction to Decimal Conversion Chart
| Fraction | Decimal |
|---|---|
| 1/2 | 0.5 |
| 1/3 | 0.3333 |
| 2/3 | 0.6667 |
| 1/4 | 0.25 |
| 3/4 | 0.75 |
| 1/5 | 0.2 |
| 2/5 | 0.4 |
| 3/5 | 0.6 |
| 4/5 | 0.8 |
| 1/6 | 0.1667 |
| 5/6 | 0.8333 |
| 1/7 | 0.1429 |
| 2/7 | 0.2857 |
| 3/7 | 0.4286 |
| 4/7 | 0.5714 |
| 5/7 | 0.7143 |
| 6/7 | 0.8571 |
| 1/8 | 0.125 |
| 3/8 | 0.375 |
| 5/8 | 0.625 |
| 7/8 | 0.875 |
| 1/9 | 0.1111 |
| 2/9 | 0.2222 |
| 4/9 | 0.4444 |
| 5/9 | 0.5556 |
| 7/9 | 0.7778 |
| 8/9 | 0.8889 |
| 1/10 | 0.1 |
| 3/10 | 0.3 |
| 7/10 | 0.7 |
| 9/10 | 0.9 |
| 1/11 | 0.0909 |
| 2/11 | 0.1818 |
| 3/11 | 0.2727 |
| 4/11 | 0.3636 |
| 5/11 | 0.4545 |
| 6/11 | 0.5455 |
| 7/11 | 0.6364 |
| 8/11 | 0.7273 |
| 9/11 | 0.8182 |
| 10/11 | 0.9091 |
| 1/12 | 0.0833 |
| 5/12 | 0.4167 |
| 7/12 | 0.5833 |
| 11/12 | 0.9167 |
| 1/13 | 0.0769 |
| 2/13 | 0.1538 |
| 3/13 | 0.2308 |
| 4/13 | 0.3077 |
| 5/13 | 0.3846 |
| 6/13 | 0.4615 |
| 7/13 | 0.5385 |
| 8/13 | 0.6154 |
| 9/13 | 0.6923 |
| 10/13 | 0.7692 |
| 11/13 | 0.8462 |
| 12/13 | 0.9231 |
| 1/14 | 0.0714 |
| 3/14 | 0.2143 |
| 5/14 | 0.3571 |
| 9/14 | 0.6429 |
| 11/14 | 0.7857 |
| 13/14 | 0.9286 |
| 1/15 | 0.0667 |
| 2/15 | 0.1333 |
| 4/15 | 0.2667 |
| 7/15 | 0.4667 |
| 8/15 | 0.5333 |
| 11/15 | 0.7333 |
| 13/15 | 0.8667 |
| 14/15 | 0.9333 |
| 1/16 | 0.0625 |
| 3/16 | 0.1875 |
| 5/16 | 0.3125 |
| 7/16 | 0.4375 |
| 9/16 | 0.5625 |
| 11/16 | 0.6875 |
| 13/16 | 0.8125 |
| 15/16 | 0.9375 |
| 1/17 | 0.0588 |
| 2/17 | 0.1176 |
| 3/17 | 0.1765 |
| 4/17 | 0.2353 |
| 5/17 | 0.2941 |
| 6/17 | 0.3529 |
| 7/17 | 0.4118 |
| 8/17 | 0.4706 |
| 9/17 | 0.5294 |
| 10/17 | 0.5882 |
| 11/17 | 0.6471 |
| 12/17 | 0.7059 |
| 13/17 | 0.7647 |
| 14/17 | 0.8235 |
| 15/17 | 0.8824 |
| 16/17 | 0.9412 |
| 1/18 | 0.0556 |
| 5/18 | 0.2778 |
| 7/18 | 0.3889 |
| 11/18 | 0.6111 |
| 13/18 | 0.7222 |
| 17/18 | 0.9444 |
| 1/19 | 0.0526 |
| 2/19 | 0.1053 |
| 3/19 | 0.1579 |
| 4/19 | 0.2105 |
| 5/19 | 0.2632 |
| 6/19 | 0.3158 |
| 7/19 | 0.3684 |
| 8/19 | 0.4211 |
| 9/19 | 0.4737 |
| 10/19 | 0.5263 |
| 11/19 | 0.5789 |
| 12/19 | 0.6316 |
| 13/19 | 0.6842 |
| 14/19 | 0.7368 |
| 15/19 | 0.7895 |
| 16/19 | 0.8421 |
| 17/19 | 0.8947 |
| 18/19 | 0.9474 |
| 1/20 | 0.05 |
| 3/20 | 0.15 |
| 7/20 | 0.35 |
| 9/20 | 0.45 |
| 11/20 | 0.55 |
| 13/20 | 0.65 |
| 17/20 | 0.85 |
| 19/20 | 0.95 |
See our inch fraction calculator for a comprehensive inch fraction to decimal chart.
You’ll probably also find our equivalent fraction chart useful.
How to Convert Mixed Fractions to Decimal
All four of these methods work for proper and improper fractions, but they don’t support mixed fractions. A mixed fraction is a whole number in front of a fraction, like this:
1 3 / 4
So, when working with mixed numbers, the first step is to convert them to an improper fraction. You can convert a mixed fraction to an improper fraction easily.
First, multiply the whole number by the fraction denominator and create a new fraction with the result as the numerator over the existing denominator. Then, add the fractions together.
1 3 / 4 = 1 × 4 / 4 + 3 / 4
1 3 / 4 = 4 / 4 + 3 / 4
1 3 / 4 = 7 / 4
Then, after the mixed number is in improper fraction form, you can convert it to a decimal number using any of the methods above.
Sample Fraction Conversions
Frequently Asked Questions
Why do you divide a fraction to make it a decimal?
Since decimals and fractions represent the same quantity but in different forms, we can divide the numerator by the denominator, which finds the quotient of the fraction. This is a representation of the same quantity!
When do you need to convert fractions to decimals?
Fractions and decimals represent the same quantity, but decimals are more convenient for certain calculations, comparisons, and measurements.
Converting fractions to decimals can be useful in situations where decimals are preferred, such as in communication or scientific fields, and for performing mathematical operations or working with measurement values.
Can every fraction be converted to a decimal?
All fractions can be converted to a decimal. However, not every fraction can be converted to a decimal that terminates or ends after a finite number of decimal places.
Some fractions have decimal equivalents that repeat infinitely, such as 1/3 (which is equivalent to 0.3333… with the 3s repeating indefinitely). These are called repeating decimals.