Fraction Calculator – Ultimate Fraction Solver
Use the fraction calculator below to add, subtract, multiply, divide, compare, or simplify fractions.
Result as a Fraction:
Result as a Decimal:
Steps to Solve Expression with Fractions
Steps to Compare Fractions and Numbers
Steps to Simplify Fraction
On this page:
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
Bailey is an experienced educator and specializes in K-12 math and science. She holds a Master's degree in professional education and holds several teaching certifications.
How to Calculate Fractions
A fraction is a numerical value that is not a whole number. It generally represents a portion of a whole, for instance, one slice of a pie.
The calculator above makes it easy to add, subtract, multiply, or divide fractions, and even shows all of the work.
But how do you calculate fractions without a calculator? See the guides below to learn how to add and subtract, multiply, or divide them.
How to Add & Subtract Fractions
Adding and subtracting fractions is a little different from adding whole numbers. You can use the following formula to add two fractions:
a / b + c / d = ad + bc / bd
Thus, to add two fractions, complete the following:
- Multiply the numerator of the first fraction a with the denominator of the second fraction d.
- Multiply the denominator of the first fraction b with the numerator of the second fraction c.
- Add the products from step 1 and step 2 (ad + bc).
- Divide the sum from step 3 (ad + bc) by the product of the denominators of both fractions (b and d).
This formula is a simple method to make the denominators of both fractions match before adding the numerators. After using the formula, you’ll need to simplify the result.
There are three steps you can use to put this formula to practice to add or subtract fractions.
Step One: Convert to Fractions with a Common Denominator
When adding fractions, the first step is to ensure that they have the same denominator. Convert each fraction to an equivalent fraction with a matching denominator to the other. To do this, you need to find the lowest common denominator (LCD), which is the smallest number that both denominators can divide into evenly.
Once you have found the lowest common denominator, you will then find what multiple you need to multiply each fraction to make the denominators match. To do this, divide the LCD by the denominator of each fraction.
Then, multiply both the numerator and denominator by the multiple to find the equivalent fractions with matching denominators.
For example, let’s convert the fractions 1 / 3 and 1 / 4 to fractions with the same denominator.
1 / 3 = 1 × 4 / 3 × 4 = 4 / 12
1 / 4 = 1 × 3 / 4 × 3 = 3 / 12
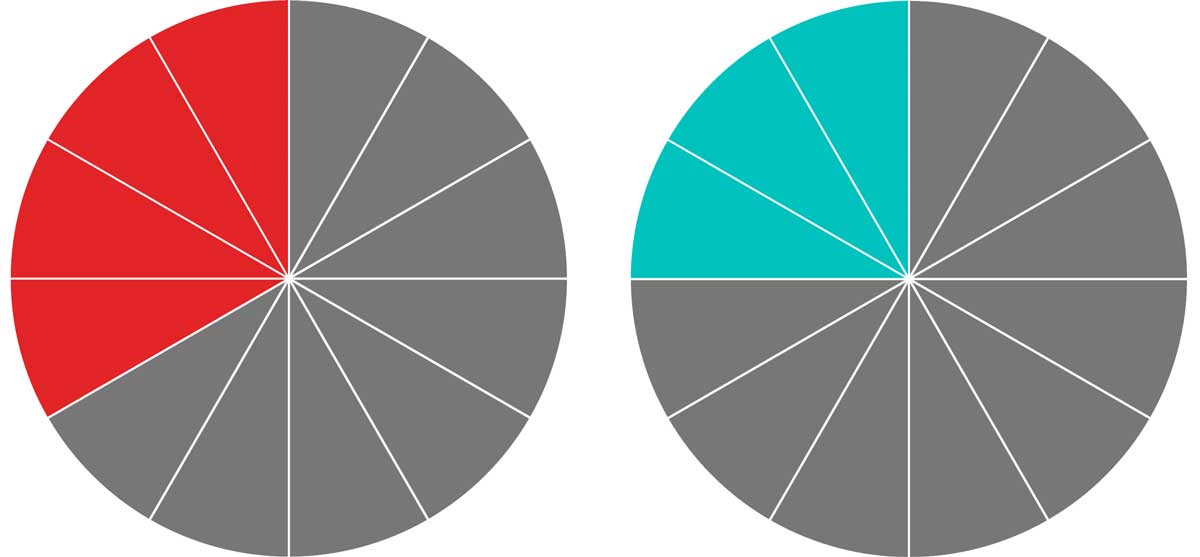
Step Two: Add or Subtract the Numerators
Once the denominators are all the same, adding and subtracting fractions is as simple as adding or subtracting the numerators.
To add the fractions, add the numerators together and put them over the common denominator.
To subtract, find the difference between the numerators and put the difference over the common denominator.
For example, continuing the previous example, let’s add 4 / 12 & 3 / 12.
4 / 12 + 3 / 12 = 4 + 3 / 12 = 7 / 12
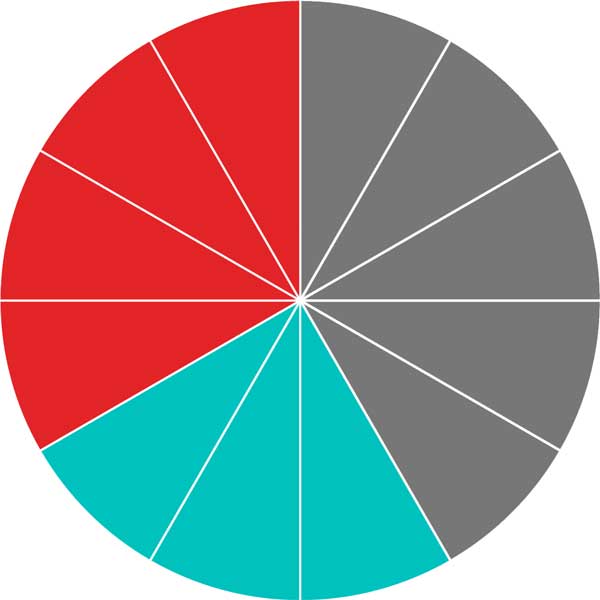
Step Three: Simplify the Fraction
The final step to adding or subtracting fractions is to simplify the result fraction. Start by finding the greatest common factor of both the numerator and the denominator. Learn more about finding the greatest common factor for more details.
Then, divide both the numerator and denominator by the greatest common factor to reduce. Or, just use our fraction simplifier to simplify and see all the work needed to do so.
You can also use our adding or subtracting calculators to easily add and subtract fractions.
How to Multiply Fractions
You can multiply fractions using the following formula:
a / b × c / d = ac / bd
You can multiply two fractions by multiplying their numerators together and their denominators together. This can also be expressed as dividing the product of the two numerators by the product of the two denominators.
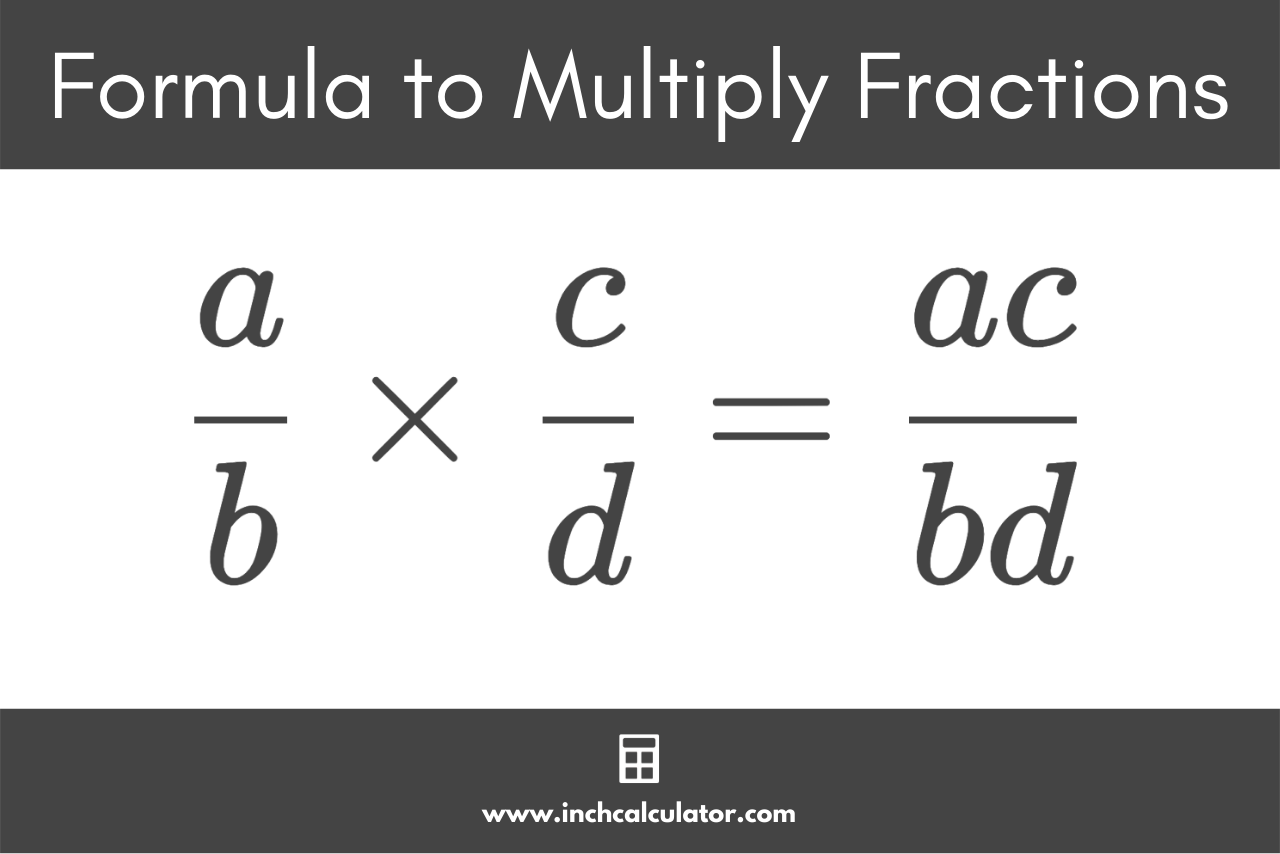
Use the following process to multiply two fractions using this formula.
Step One: Multiply the Numerators and Denominators
The first step is to multiply the numerators together and multiply the denominators together. The result might be an improper fraction, but we’ll reduce it in the next step.
For example, let’s multiply 2 / 3 × 3 / 4.
2 / 3 × 3 / 4 = (2 × 3) / (3 × 4)
2 / 3 × 3 / 4 = 6 / 12
Step Two: Simplify the Fraction
Like adding and subtracting, the final step of multiplying fractions is to simplify. To simplify, find the numerator and denominator’s greatest common factor, then divide both of them by the common factor.
To simplify 6 / 12, find the greatest common factor.
The greatest common factor of 6 and 12 is 6.
Next, divide both the numerator and denominator by the greatest common factor.
6 / 12 = (6 ÷ 6) / (12 ÷ 6)
6 / 12 = 1 / 2
How to Divide Fractions
To divide fractions, you can multiply the first fraction by the reciprocal of the second fraction. A reciprocal fraction is the fraction that results when you invert or “flip” the numerator and denominator.
For instance, the reciprocal of 1/2 is 2/1.
Once you have found the reciprocal of the second fraction, you can multiply the numerators and denominators of both fractions together.
How does this work?
Think about 6 ÷ 2.
We know that 6 divided by 2 is equal to 3.
Now, multiply by the reciprocal.
6 × 1 / 2 = 6 / 2
6 / 2 = 3
An easy way to remember this method is “keep, change, flip.”
- Keep: Keep the first fraction as is.
- Change: Change the division symbol to multiplication.
- Flip: “Flip” – or find the reciprocal of the second fraction.
For example:
1 / 2 ÷ 3 / 4 = 1 / 2 × 4 / 3
1 / 2 × 4 / 3 = 4 / 6
4 / 6 = 2 / 3
1 / 2 ÷ 3 / 4 = 2 / 3
You can also divide fractions using the following formula:
a / b ÷ c / d = ad / bc
To divide fractions, divide the product of the first fraction numerator a and second fraction denominator d by the product of the first fraction denominator b and second fraction numerator c.
This is known as cross multiplying because you cross-multiply the numerators with the opposite denominators.
The following steps show how to divide fractions using this formula.
Step One: Multiply Each Numerator by the Opposite Denominator
To divide one fraction by another, start by multiplying the first numerator by the second denominator. Then multiply the second numerator by the first denominator.
For example, let’s divide 2 / 3 by 3 / 4.
2 / 3 ÷ 3 / 4= (2 × 4) / (3 × 3)
2 / 3 ÷ 3 / 4= 8 / 9
Step Two: Simplify the Fraction
Just like when multiplying fractions, the final step of dividing them is to simplify the fraction. See the instructions to simplify a fraction above.
How to Calculate Mixed Numbers
Mixed numbers might seem intimidating, but the process of calculating them is nearly the same as a normal fraction with one extra step. As a refresher, a mixed number is a number consisting of a whole number and a proper fraction.
The first thing to do when calculating a mixed number is to remove the whole number and increase the numerator of the fraction to make it an improper fraction.
Start by multiplying the whole number by the denominator.
Then, add the result to the numerator in the remaining fraction. You can always use our mixed number to fraction calculator for this step.
Continue following the steps above to calculate fractions after moving the result to the numerator.
For example, let’s convert the mixed number 2 2 / 5 to an improper fraction.
Multiply the whole number by the denominator.
2 × 5 = 10
Add the result to the numerator.
10 + 2 = 12
Rewrite the fraction.
2 2 / 5 = 12 / 5
How to Calculate Negative Fractions
A negative fraction is one that is denoted with a minus sign in front. The negative sign can be placed in front of the fraction, aligned with the fraction bar, or it can be in front of the numerator or denominator.
–a / b = -a / b = a / -b
When the numerator and the denominator both have a negative sign in front, then the fraction is actually positive. Negative fractions should only have one negative sign.
Because the negative sign can be in several places, it is most helpful to put the sign on the numerator. This allows you to use any of the formulas above to add or subtract a negative fraction.
When you place the negative sign in front of the numerator, you can use any of the formulas or steps above to calculate a fraction normally.
Here is an overview for calculating negative fractions:
Negative fractions follow the same rules as positive fractions when it comes to addition, subtraction, multiplication, and division. However, there are some additional rules to keep in mind when dealing with negative fractions:
- The product of two negative numbers is positive.
- The product of a positive and a negative number is negative.
- The quotient of two negative numbers is positive.
- The quotient of a positive and a negative number is negative.
Frequently Asked Questions
What are the 3 types of fractions?
There are three types of fractions: proper fractions, improper fractions, and mixed fractions. Proper fractions have a numerator that is smaller than the denominator, improper fractions have a numerator that is equal to or larger than the denominator, and mixed fractions combine a whole number and a proper fraction.
Why do we use fractions?
Fractions are used to represent parts of a whole or a collection, to compare and order quantities, and to perform mathematical operations. They are used in various fields to express precise values and ratios, and in everyday life for cooking, measuring, and sharing.
What is the golden rule of fractions?
The golden rule of fractions is to always keep the denominator the same when adding or subtracting fractions, which is done by finding a common denominator. This makes it easier to add, subtract, or compare fractions without changing their value.