Decimal to Fraction Calculator
Convert a decimal to fraction form using the calculator below. The calculator shows all the work in the solution so you can see how to do the conversion step-by-step.
Fraction:
Steps to Solve
On this page:
- How to Convert a Decimal to a Fraction
- Step One: Create the Starting Fraction
- Step Two: Multiply by Ten
- Step Three: Reduce the Fraction
- How to Convert a Repeating Decimal to a Fraction
- How to Convert a Negative Decimal to a Fraction
- Decimal to Fraction Chart
- More Decimal to Fraction Conversions
- Frequently Asked Questions
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
Bailey is an experienced educator and specializes in K-12 math and science. She holds a Master's degree in professional education and holds several teaching certifications.
How to Convert a Decimal to a Fraction
Decimal and fractional numbers both represent a number that is not an even integer or a number that is not a whole number. You might be wondering how to turn a decimal into a fraction.
Every decimal number can be converted to a fraction in just three easy steps.
Note that the process of converting a repeating decimal is different.
Step One: Create the Starting Fraction
The first step in transforming a decimal to a fraction is creating a starting fraction with the decimal as the top number and 1 as the bottom number.
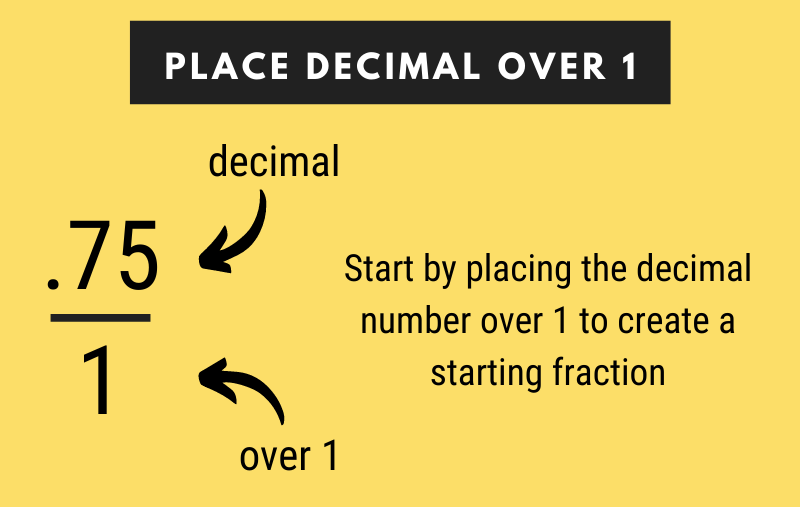
For example, to convert .75 to a fraction, start by making a fraction with .75 as the numerator and 1 as the denominator.
.75 = .75 / 1
Step Two: Multiply by Ten
The next step is to multiply the numerator and the denominator by 10 to eliminate the decimal place. Continue multiplying both by 10 until the numerator is a whole number.
Continuing the example from above, let’s convert .75 / 1 to 75 / 100 using multiplication by 10.
.75 / 1 = (.75 × 10) / (1 × 10) = 7.5 / 10
7.5 / 10 = (7.5 × 10) / (10 × 10) = 75 / 100
Step Three: Reduce the Fraction
The final step in converting a decimal to a fraction is to reduce the fraction to its simplest form. To reduce, find the greatest common factor for the numerator and denominator.
Then, divide both the numerator and the denominator by the greatest common factor. The greatest common factor is sometimes also called the greatest common divisor (GCD) or highest common factor (HCF).
To complete the example above, we know that the greatest common factor of 75 and 100 is 25. So, let’s divide the numerator and denominator by 25 to simplify the fraction.
75 / 100 = (75 ÷ 25) / (100 ÷ 25)
75 / 100 = 3 / 4
Here’s a tip: use our fraction simplifier to easily reduce your fraction.
Decimal values larger than 1 result in a numerator that is larger than the denominator. These are called improper fractions, and they can be converted to a mixed number (also called mixed fractions).
To convert a decimal to a mixed number, divide the numerator by the denominator and set the resulting quotient as the whole number. Then use the remainder for the numerator in the mixed fraction.
For example, let’s simplify the improper fraction 5 / 4 to a mixed number.
5 / 4 = 5 ÷ 4 = 1 R1
5 / 4 = 1 1 / 4
You can also use a fraction to mixed fraction calculator for this step.
For negative numbers, remove the negative symbol from the starting decimal, then follow the steps above. After converting to fraction form, add the negative sign back.
How to Convert a Repeating Decimal to a Fraction
So far we’ve been talking about terminating decimal numbers, since the numbers have a finite number of digits after the decimal. But some decimals are repeating decimals, which are numbers that continue infinitely after the decimal point, such as 1.1787878.
These numbers can be expressed in a rounded form, such as 1.788, or with an over-bar above the repeating portion like this: 1.178.
Repeating decimal numbers require a slightly different process to convert to a fraction.
Step One: Create an Equation
The first step in transforming a repeating decimal is to create an algebraic equation to represent the decimal.
For example, let’s convert the decimal 1.178 into a fraction. Start by creating an equation to assign the expression 1.1787878 to x.
x = 1.1787878
Step Two: Multiply by 10 Until the Repeating Decimal is on the Left
The second step is to continue multiplying both sides of the equation by 10 until the repeating number is on the left side of the decimal point.
If there are multiple repeating numbers that repeat in a pattern, then multiply by 10 until the repeating pattern is on the left side of the decimal point.
Continuing the example above, let’s multiply both sides of the equation by 10 until the repeating “78” part of the decimal is on the left side of the decimal point.
x = 1.1787878
10 × x = 10 × 1.1787878
10x = 11.787878
10 × 10x = 10 × 11.787878
100x = 117.87878
10 × 100x = 10 × 117.87878
1000x = 1178.78
Step Three: Multiply by 10 Until the Repeating Decimal is on the Right
The third step is to create a new equation for x and multiply until the repeating decimal portion is to the right of the decimal point
Building on our example, multiply both sides of the equation by 10 until the repeating “78” part of the decimal is on the right side of the decimal point.
x = 1.1787878
10 × x = 10 × 1.1787878
10x = 11.78
Step Four: Combine the Equations
The next step is to combine the equations and move both x variables to the left and both decimal values to the right.
Let’s combine the equations and solve.
1000x – 10x = 1178.78 – 11.788
Step Five: Solve
Finally, solve for x to convert the decimal value to a fraction.
Let’s combine the equations and solve.
1000x – 10x = 1178.78 – 11.78
990x = 1167
990x / 990 = 1167 / 990
x = 1167 / 990
How to Convert a Negative Decimal to a Fraction
You can convert a negative decimal to a fraction too. Start by removing the minus sign from the beginning of the number.
Then, convert the number to fraction form following the steps above.
And finally, add the negative sign in front of the fraction to convey that this is a negative number. And that’s all there is to it.
Decimal to Fraction Chart
An alternate method to convert a decimal to a fraction is to use a conversion chart such as this one. See the fraction equivalents for some common decimal values below. The table allows you to conveniently see the corresponding fraction for a decimal number.
| Decimal Value | Fraction Value |
|---|---|
| 0.0625 | 1/16 |
| 0.08333 | 1/12 |
| 0.1 | 1/10 |
| 0.111 | 1/9 |
| 0.125 | 1/8 |
| 0.1666 | 1/6 |
| 0.2 | 1/5 |
| 0.222 | 2/9 |
| 0.25 | 1/4 |
| 0.333 | 1/3 |
| 0.375 | 3/8 |
| 0.4 | 2/5 |
| 0.444 | 4/9 |
| 0.5 | 1/2 |
| 0.555 | 5/9 |
| 0.6 | 3/5 |
| 0.625 | 5/8 |
| 0.666 | 2/3 |
| 0.75 | 3/4 |
| 0.777 | 7/9 |
| 0.8 | 4/5 |
| 0.8333 | 5/6 |
| 0.875 | 7/8 |
| 0.888 | 8/9 |
| 0.9 | 9/10 |
More Decimal to Fraction Conversions
See the steps to convert these common decimal values to fraction form.
See more decimals and their equivalent fractions.
Frequently Asked Questions
When do you need to convert decimals to fractions?
Converting decimals to fractions can make calculations easier, comparisons clearer, and improve communication in some situations.
For instance, decimals can be converted to fractions when simplifying calculations, comparing values or expressing a quantity in a way that is more appropriate for a particular context, such as specifying the slope of a ramp in construction projects.
What are the benefits of using fractions over decimals?
Fractions have several advantages over decimals in certain situations. They are often easier to understand, especially for those unfamiliar with decimal notation, and can be more precise in certain calculations, such as in construction.
Fractions are also compatible with traditional measuring systems like inches and feet and can simplify calculations, making them useful for communicating information clearly, such as in recipes or baking measurements.
How do you convert a decimal greater than 1 to a fraction?
To convert a decimal greater than 1 to a fraction, follow these steps:
- Count the number of decimal places in the decimal.
- Write the decimal as a fraction with the denominator as 1 followed by the same number of zeros as the number of decimal places.
- Simplify the fraction by dividing both the numerator and denominator by their greatest common factor (GCF).