LCD Calculator (Least Common Denominator)
Find the least common denominator for a set of fractions using the LCD calculator below.
Least Common Denominator:
Steps to Solve
On this page:
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
Bailey is an experienced educator and specializes in K-12 math and science. She holds a Master's degree in professional education and holds several teaching certifications.
How to Find the Least Common Denominator
A denominator is the bottom number of a fraction, or the number below the fraction line. For a fraction 1/3, the denominator is 3.
A common denominator is a denominator that is common to the fractions being operated on. For the denominator to be common, it must be the same in all fractions.
For instance, 1/3 and 2/3 have common denominators – the denominators are the same.
1/3 and 2/5 do not have common denominators – the denominators are different.
The least common denominator is the smallest common denominator. It is the smallest whole number that is evenly divisible by all uncommon denominators. The least common denominator is also referred to as the lowest common denominator or the least common multiple.
The least common denominator for the fractions 1/3 and 2/5 is 15.
15 ÷ 3 = 5
15 ÷ 5 = 3
Note that there can be no remainder when dividing one of the denominators by the least common denominator.
There are a few methods that you can use to find the least common denominator. The easiest is to use the calculator above. If you want to do the work yourself, follow along to learn two methods to solve it.
Method One: Find the Least Common Denominator Using Factorization
One way to find the least common denominator is to use prime factorization. Find the prime factors of each denominator. Then multiply all of the prime factors, taking the common factors only once, to find the least common denominator.
You can use our prime factorization calculator to find the prime factors for each number.
Example: Find the Least Common Denominator of 10 and 15
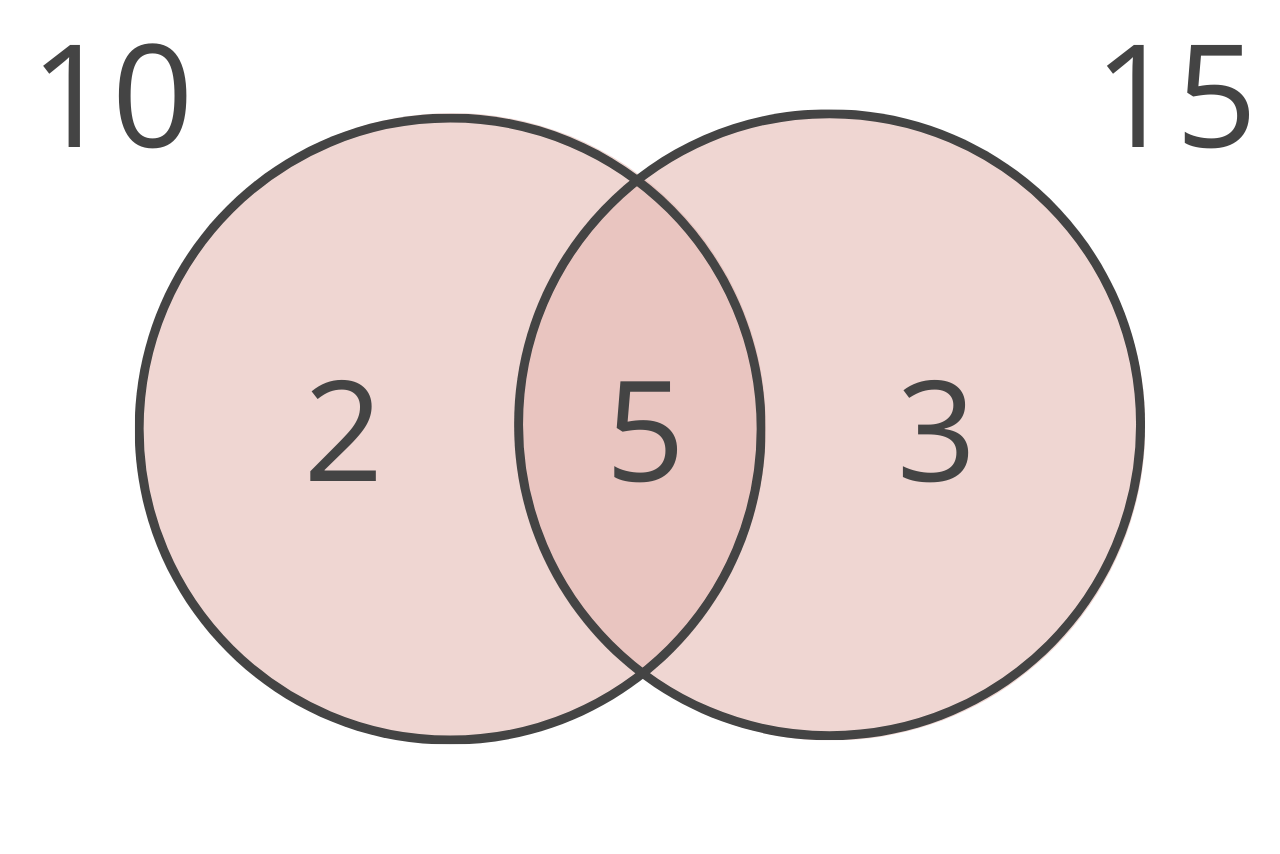
Step one: find the prime factors of 10.
To find the prime factors of 10, you can begin by dividing 10 by the smallest prime number, which is 2. Since 10 is even, it is divisible by 2. 10 divided by 2 is equal to 5. Since 5 is a prime number, we cannot divide it any further.
Therefore, the prime factors of 10 are 2 and 5.
Step two: find the prime factors of 15.
To find the prime factors of 15, you can begin by dividing 15 by the smallest prime number, which is 2. However, 15 is an odd number and is not divisible by 2.
Then you can divide 15 by the next smallest prime number, which is 3. 15 divided by 3 is equal to 5. Since 5 is a prime number, we cannot divide it any further.
Therefore, the prime factors of 15 are 3 and 5.
Step three: find the prime factors that are common to both 10 and 15, then remove the ones that are common to both from the list.
The prime factors of 15 and 10 are 5, 3, & 2.
Step four: multiply the factors together to find the least common denominator. Note that since 5 is common between 10 and 15 it is only used once.
LCD = 5 × 3 × 2
LCD = 30
Method Two: Find the Least Common Denominator by Finding all Multiples
You can also find the least common denominator by finding all of the multiples of each denominator, then identifying the smallest one that is common to both of them.
To find multiples, start by multiplying it by 2 to find the first multiple, then multiply it by 3 to find the second, and so on. Continue by multiplying by larger numbers to find all of the multiples.
Then, repeat this for each denominator.
For example, let’s find the least common denominator of 10 and 15 by finding all multiples.
The multiples of 10 are [10,20,30,40,50,60,…]
The multiples of 15 are [15,30,45,60,75,…]
Observe that the multiples that are common to both 10 and 15 are 30 and 60. The smallest of these is 30, which makes it the least common denominator.
Thus, the least common denominator of 10 and 15 is 30.
Method Three: Find the LCD Using Division
You can also find the least common denominator using division.
Begin by writing the denominators as factors and divide out the common factors.
For example, if we want to find the LCD of 1/3 and 2/5:
3 = 3 × 1
5 = 5 × 1
Multiply the remaining factors together.
3 × 5 = 15
The product 15 is the least common multiple (LCM) of 3 and 5, so it is also the least common denominator (LCD).
You can then rewrite each fraction with the LCD as the denominator by multiplying both the numerator and denominator by the factor needed to obtain the LCD.
1 / 3 = 5 / 15
2 / 5 = 6 / 15
So the LCD is 15, and the equivalent fractions with the LCD as the denominator are 5/15 and 6/15.
Frequently Asked Questions
What is the least common denominator used for?
The least common denominator (LCD) is the smallest number that is a multiple of the denominators of two or more fractions. It is used in fraction operations and is used to convert fractions to equivalent fractions with the same denominator.
When you find the LCD and convert the fractions, you can add or subtract fractions easily without changing their values.
Are LCD and LCM the same thing?
LCD (least common denominator) and LCM (least common multiple) are not the same, although they are related.
The LCD is the smallest common multiple of the denominators of two or more fractions, which is used to find a common denominator for the fractions, whereas the LCM is the smallest multiple that is common to two or more numbers.
What is the difference between LCD and GCF?
The GCF is the largest factor common to two or more numbers, and it is used to simplify fractions, while the LCD is used to find a common denominator in fraction operations. Although both concepts are used in math, they serve different purposes.