Prime Factorization Calculator
Find the prime factors for a number, including large numbers, by entering the number below. The calculator will also indicate if the number is a prime number or not.
Prime Factors:
Solution
132 = 22 × 31 × 111
On this page:
How To Find Prime Factors
The prime factors of a number are a set of prime numbers that, when multiplied together, equal the number.
A prime number is a number that is only divisible by itself and 1.
Prime factorization of a number is the act of finding all of the prime factors of a number. This process is also known as Prime Decomposition.
There is no mathematical formula for finding all the prime factors of any number. In fact, mathematicians wonder if there is a largest prime number and are using computer algorithms to try and find it if it exists, but so far, one has not been found.
Trial Division Method
One method of prime factorization is called the trial division method. To use this method to find all the prime factors of a number, say x, for example, start by dividing x by any prime number.
If the resulting value is not a whole number, then that prime number is not a prime factor of x. If it is, then divide the result by another prime number. Continue this process until the final result is also a prime number.
That is, the final result should only be divisible by itself and 1
This method is often visualized using a factor tree (see the diagram below for an example). The original number sits atop the tree, and its divisors are the branches. The ends of all the branches are the prime factors of the original number.
How do we know which prime numbers to use when dividing the original number? This will take some trial and error, hence the name Trial Division Method. A good strategy is to determine if the number is even or odd.
If even, start by dividing the number by 2 and continue to do so until the resulting value is odd, then try to divide by 3, then 5, and so on. Any prime number that you use to divide either the original number or a resulting value is a prime factor of the original number.
To know which numbers are prime that you should try dividing the original number by, see the list of all of the prime numbers under 1000 below as a helpful reference.
As you divide the original number and resulting factors by prime numbers following the example below, you’ll see that you will be creating your own factor tree!
You might also find our greatest common factor calculator helpful to find all factors for a number.
For example, let’s find the prime factors of the number 132.
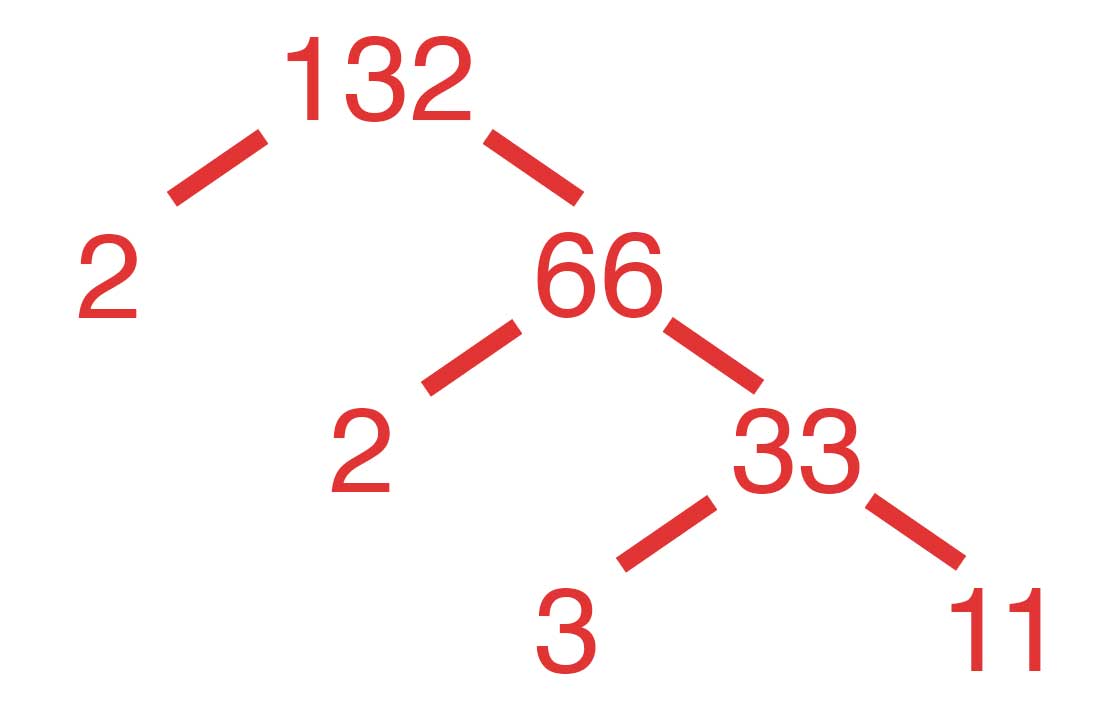
Since 132 is an even number, start by dividing 132 by 2, which equals 66. 2 is a prime number and cannot be divided further, so it is a prime factor.
However, 66 can be divided by 2 again to get 33. Now we have another 2 as a prime factor.
We can divide 33 by 3 to get 11. 3 is a prime number, so it’s also a prime factor. 11 cannot be divided again and so it is also a prime factor.
Putting it all together, the prime factors of 132 are [11,3,2,2]. These are all prime numbers, and if we multiply them all together, we’ll get 132.
List of Prime Factors Under 1,000
| 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 |
| 31 | 37 | 41 | 43 | 47 | 53 | 59 | 61 | 67 | 71 |
| 73 | 79 | 83 | 89 | 97 | 101 | 103 | 107 | 109 | 113 |
| 127 | 131 | 137 | 139 | 149 | 151 | 157 | 163 | 167 | 173 |
| 179 | 181 | 191 | 193 | 197 | 199 | 211 | 223 | 227 | 229 |
| 233 | 239 | 241 | 251 | 257 | 263 | 269 | 271 | 277 | 281 |
| 283 | 293 | 307 | 311 | 313 | 317 | 331 | 337 | 347 | 349 |
| 353 | 359 | 367 | 373 | 379 | 383 | 389 | 397 | 401 | 409 |
| 419 | 421 | 431 | 433 | 439 | 443 | 449 | 457 | 461 | 463 |
| 467 | 479 | 487 | 491 | 499 | 503 | 509 | 521 | 523 | 541 |
| 547 | 557 | 563 | 569 | 571 | 577 | 587 | 593 | 599 | 601 |
| 607 | 613 | 617 | 619 | 631 | 641 | 643 | 647 | 653 | 659 |
| 661 | 673 | 677 | 683 | 691 | 701 | 709 | 719 | 727 | 733 |
| 739 | 743 | 751 | 757 | 761 | 769 | 773 | 787 | 797 | 809 |
| 811 | 821 | 823 | 827 | 829 | 839 | 853 | 857 | 859 | 863 |
| 877 | 881 | 883 | 887 | 907 | 911 | 919 | 929 | 937 | 941 |
| 947 | 953 | 967 | 971 | 977 | 983 | 991 | 997 |
Frequently Asked Questions
Do all numbers have prime factors?
Yes! In fact, the Fundamental Theorem of Arithmetic states that every integer greater than one can be written as a product of prime numbers.
What is prime factorization used for?
Prime factorization is used for finding the least common multiple of multiple numbers, for example, when combining fractions. In addition, it’s also used in cryptography to help protect digital codes on computers.
Can negative numbers be prime factors?
By definition, all prime numbers are positive, so generally no, negative numbers cannot be prime factors. However, prime numbers can be negative if they are defined such that they are prime if they can only be divided by -1 and itself.
Except for rare cases, you probably won’t encounter negative prime factors.


