Long Division Calculator – with Steps to Solve
Enter the divisor and dividend below to calculate the quotient and remainder using long division. The results and steps to solve it are shown below.
Result:
| Full Answer: | 18 R 3
|
|---|---|
| Quotient: | 18
|
| Remainder: | 3
|
Solution
| 1 | 8 | ||
| 4 | 7 | 5 | |
| - | 4 | ||
| 3 | 5 | ||
| - | 3 | 2 | |
| 3 |
On this page:
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
Ethan has a PhD in astrophysics and is currently a satellite imaging scientist. He specializes in math, science, and astrophysics.
How to Do Long Division with Remainders
Learning long division is a crucial milestone in understanding essential math skills and a rite of passage to completing elementary school. It strikes fear in elementary school students and parents alike.
A recent study found that the understanding of long division and fractions in elementary school is directly linked to the student’s ability to learn and understand algebra later in school.[1]
Have no fear!
Learning long division can be easy, and in just a few easy steps, you can solve any long division problem. Follow along as we break it down, but first, we need to cover the anatomy of a long division problem.
Parts of a Long Division Problem
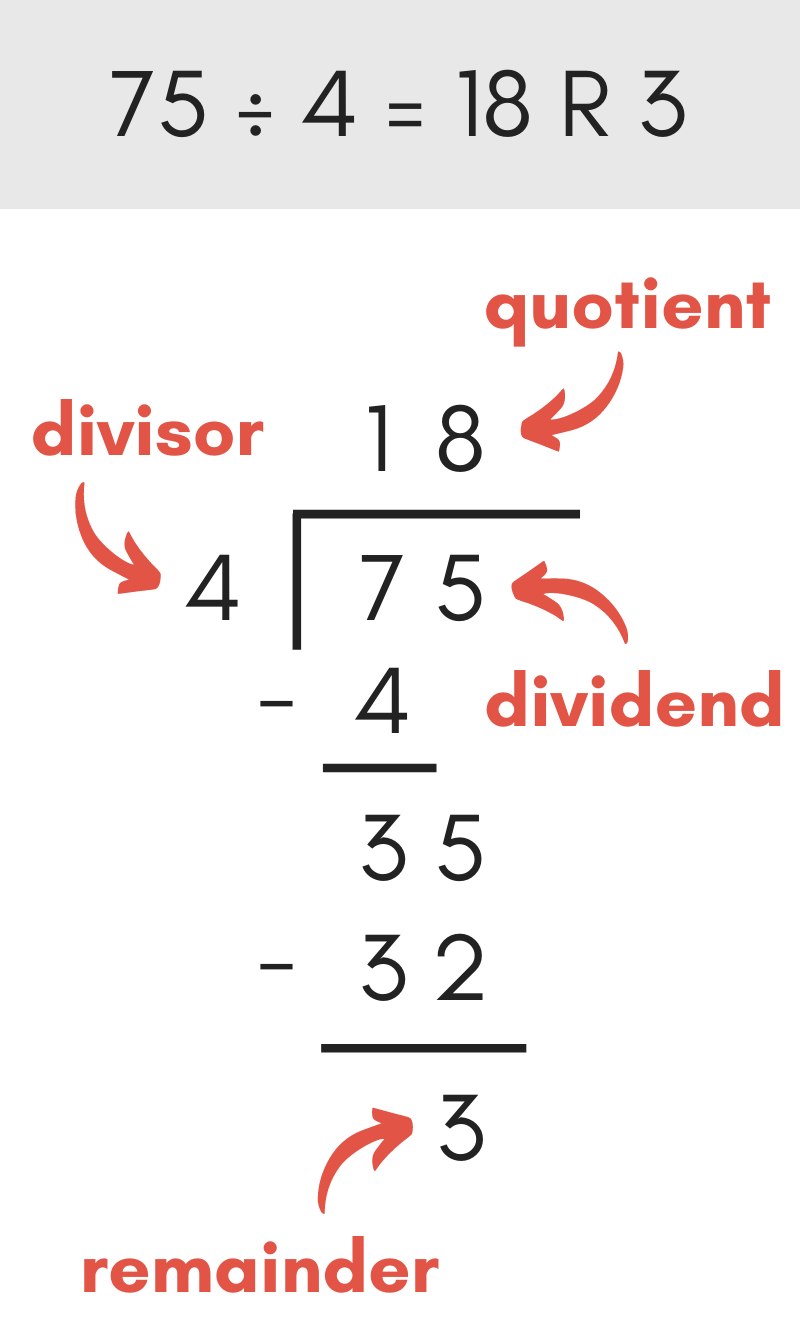
There are a few parts to a long division problem, as shown in the image above.
The dividend is the number being divided and appears to the right and under the division line.
The divisor is the number being divided by and appears to the left of the division line.
The quotient is the solution and is shown above the dividend over the division line. Often in long division, the quotient is referred to as just the whole number part of the solution.
The remainder is the remaining part of the solution, or what’s leftover, that doesn’t fit evenly into the quotient.
Steps to Calculate a Long Division Problem
There are a few main steps to solving a long division problem: divide, multiply, subtract, bringing the number down, and repeating the process.
Step One: Set up the Expression
The first step in solving a long division problem is to draw the equation that needs to be solved. If the problem is already in long division form, then skip along to step two.
If it’s not, this is how to draw the long division problem.
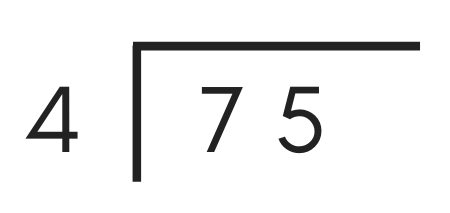
Start by drawing a vertical bar to separate the divisor and dividend and an overbar to separate the dividend and quotient.
Place the dividend to the right of the vertical bar and under the overbar. Place the divisor to the left of the vertical bar.
For example, to divide 75 by 4, the long division problem should look like this:
Step Two: Divide
With the long division problem drawn, start by dividing the first digit in the dividend by the divisor.
You can also think about this as counting the number of times the divisor will evenly fit into this digit in the dividend.
If the divisor does not fit into the first digit an even number of times, drop the remainder or decimal portion of the result and write the whole number portion of the result in the quotient above the overline directly above the digit in the dividend.
For example, the divisor “4” goes evenly into the first digit of the dividend “7” one time, so a “1” can be added to the quotient above the 7.
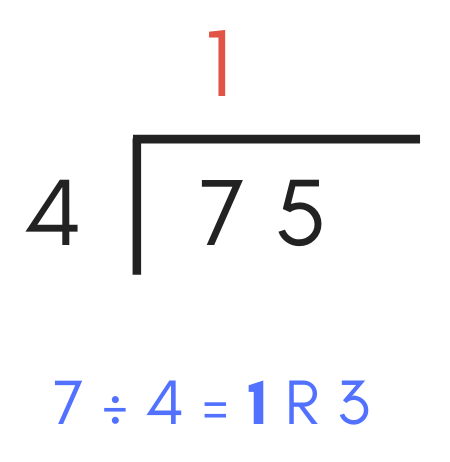
Step Three: Multiply
The next step is to multiply the divisor by the digit just added to the quotient. Write the result below the digit in the dividend.
This step forms the part of the expression for the next step.
Continuing with our example, multiplying the divisor “4” by “1”, which we found in the previous step, equals “4”. So, add a “4” below the first digit in the dividend.
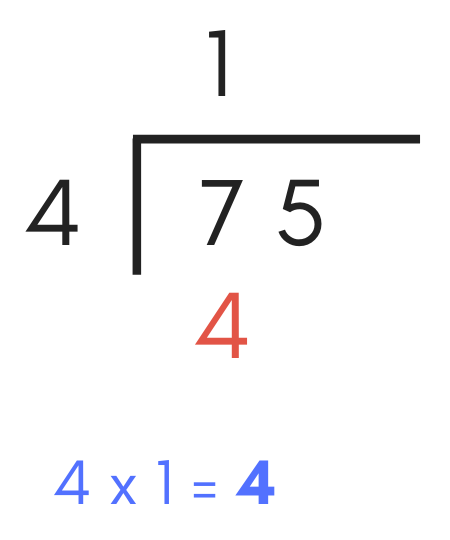
Step Four: Subtract
Now, add a minus sign “-” before the number added in the previous step and draw a line below it to form a subtraction expression.
Continuing the example above, add a “-” before the “4” and a subtraction line below it.
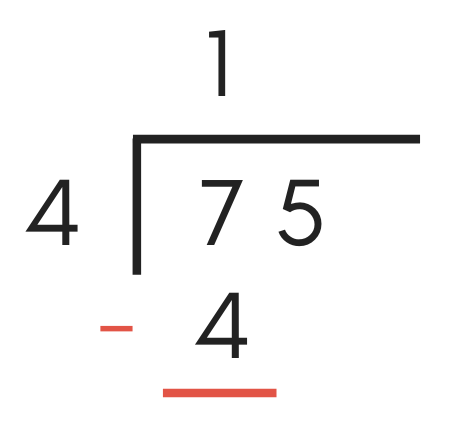
Now that you have created a subtraction problem, it’s time to solve it.
To solve, subtract “7” minus “4”, which equals “3”, so write a “3” below the subtraction line.
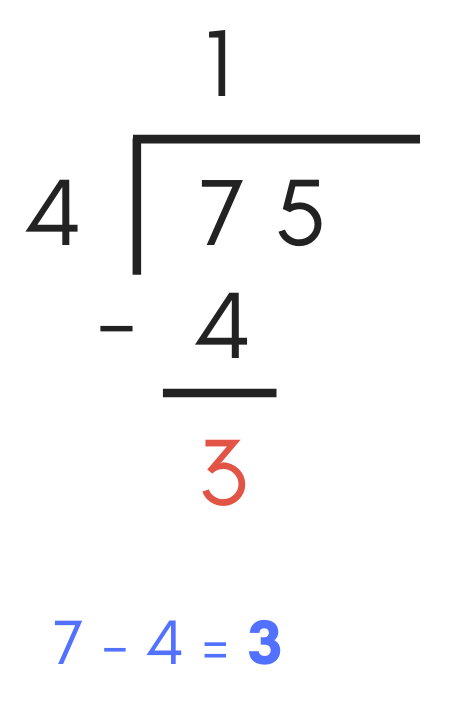
Note: if the resulting value of the subtraction problem is greater than the divisor, then you made a mistake in step 2 and should double-check your work.
If the long division problem has a dividend that is a single digit, then hooray, you’re done! The remaining number that is the result of the subtraction problem is the remainder, and the number above the dividend is the whole number quotient.
If more digits are remaining in the dividend, then proceed to the next step.
Step Five: Pull Down the Next Number
At this point in the process, it’s time to operate on the next number in the dividend. To do this, pull down the next digit in the dividend and place it directly to the right of the result from the subtraction problem above.
The next digit in the dividend is “5”. So, pull “5” down and write it next to the “3” found in the previous step.
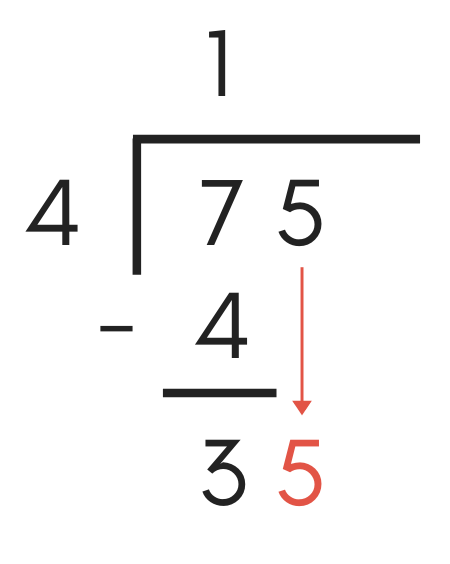
Step Six: Repeat
At this point, you might be wondering where to go from here. Repeat steps two to five until all the digits in the dividend have been pulled down, divided, multiplied, and subtracted.
When dividing, use the result of the subtraction problem combined with the pulled-down digit as the dividend and divide the divisor into it.
Continuing the examples above, divide the result of the subtraction problem and the pulled-down digit by the divisor. Thus, the next step is to divide 35 by 4. The result is “8”, so add “8” to the quotient.
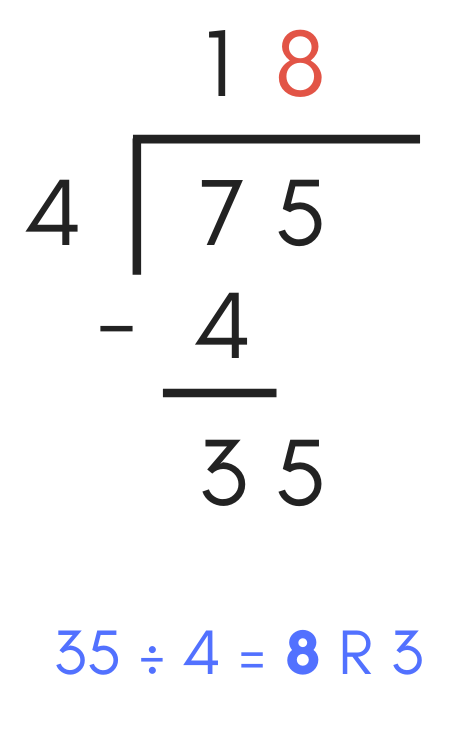
Next, multiply the quotient digit “8” by the divisor “4”, which equals 32. Add “32” to the long division problem and place a negative sign in front of it.
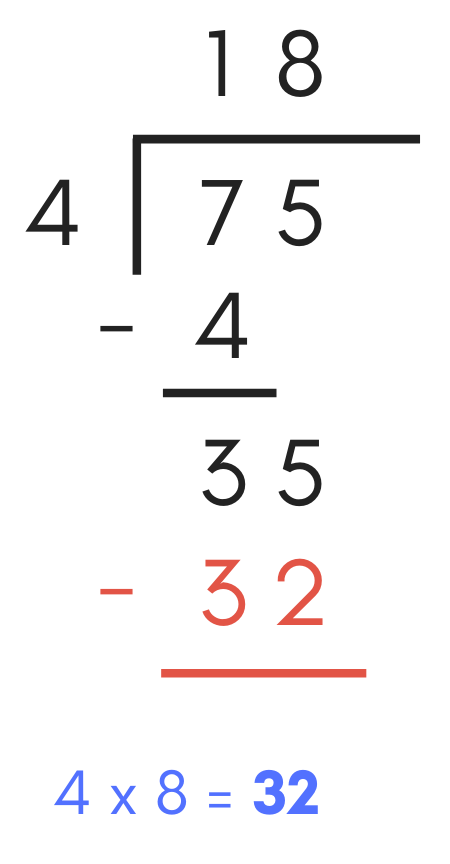
Next, repeat the subtraction process, subtracting 32 from 35, which equals 3. Add a “3” below the subtraction line. Since there are no longer any remaining digits in the dividend, this is the remainder portion of the solution.
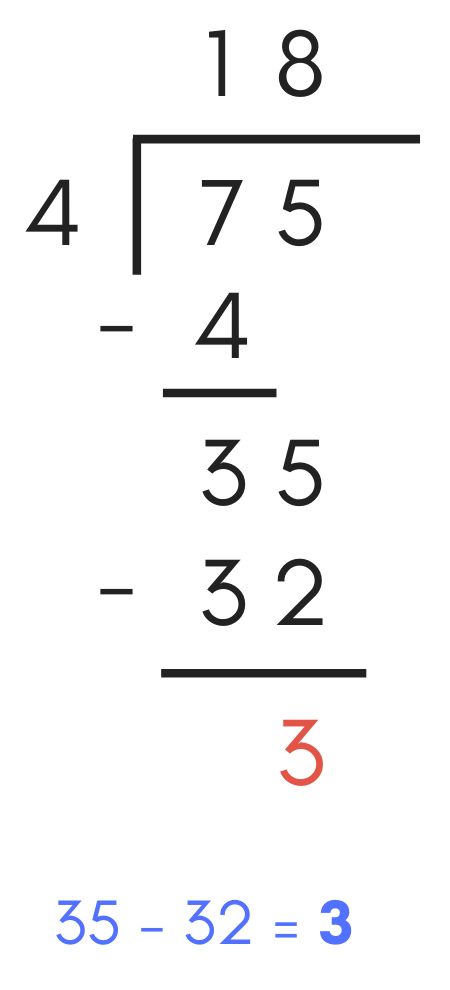
Therefore, 75 divided by 4 is 18 with a remainder of 3. As you practice these steps, use the calculator above to confirm your answer and validate your steps solving long division problems.
How to get the Quotient and Remainder as a Decimal
If you’ve gotten this far, then you should have a good idea of how to solve a long division problem, but you might be stuck if you need to get the quotient as a decimal rather than a whole number with a remainder.
To calculate the quotient in decimal form, follow the steps above the get the whole number and remainder.
Next, divide the remainder by the divisor to get the remainder as a decimal. Finally, add the decimal to the quotient to get the quotient in decimal form.
For example, 75 ÷ 4 is 18 with a remainder of 3.
Divide 3 by 4 to get the decimal 0.75.
3 ÷ 4 = 0.75
Then, add 0.75 to 18 to get the quotient as a decimal.
0.75 + 18 = 18.75
Thus, the decimal form of 75 ÷ 4 equals 18.75.
How to do Long Division Without Division
While it defeats the purpose of actually learning how to do long division, there is technically a way to perform long division without actually doing any division. The way to do this is as follows.
Step One: Set up the Expression
Set up the long division expression the exact same way as you would normally.
Step Two: Repeatedly Subtract the Divisor
Now, subtract the divisor from the dividend. Afterward, subtract the divisor again from the remaining value. Do this repeatedly until the remaining value is less than the divisor.
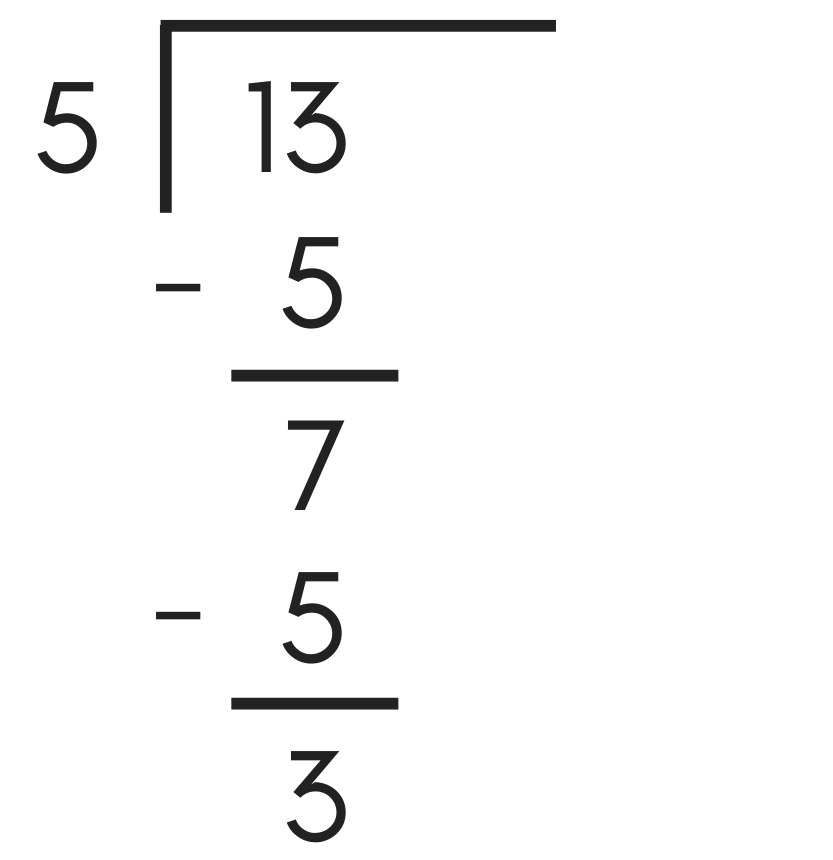
Step Three: Count the Number of Subtractions
Finally, to find the quotient, simply count the number of times you subtracted the divisor. This is the whole number portion of the quotient, and the final remaining value is the remainder.
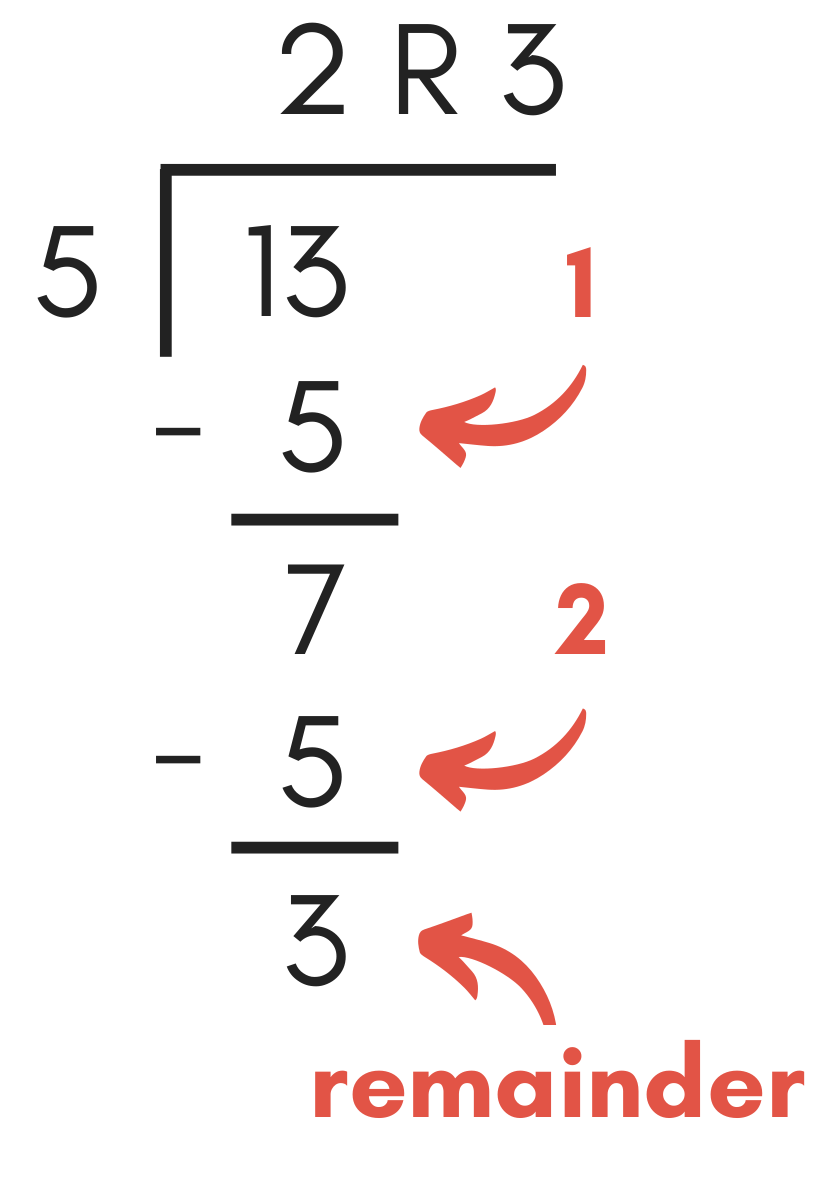
Note: While this method of solving long division problems may seem easier, it is often very impractical to do so. For example, in the above example of 75 divided by 4, you would need to repeat the subtraction 18 times!
Therefore, traditional long division is the vastly superior method.
Frequently Asked Questions
Why is long division important?
Long division is important not just because it is a tool that allows us to solve difficult division problems, but because it helps to teach logical thinking that will prepare students to excel in solving future mathematical problems.
Why do we still teach long division?
We still teach long division because it teaches students how to think logically, a valuable skill that is shown not just to improve future understanding of algebraic concepts, but also to help solve problems in all aspects of their lives.
How do you check a long division answer?
Just like subtraction is the opposite of addition, multiplication is the opposite of division. Therefore, to check a long division answer, multiply the quotient by the divisor, and if it equals the dividend, then the answer is correct!
Can you do long division on a calculator?
While a calculator can solve division problems, it will not list out the steps used in evaluating a long division problem, and will therefore not improve your understanding of how to perform long division.
References
- Carnegie Mellon University, Press Release: Carnegie Mellon-Led Research Team Finds Knowledge Of Fractions and Long Division Predicts Long-Term Math Success, https://www.cmu.edu/news/stories/archives/2012/june/june15_mathsuccess.html