Slope-Intercept Form Calculator
Express the equation of a line in slope-intercept form using the calculator below. Use two known points on the line, the slope and y-intercept, or the slope and one known point on the line.
Slope-Intercept Form:
Line Graph:
Steps to Find Slope-Intercept Form
Step One: Calculate the Slope
Step Two: Find the y-Intercept (b)
Step Three: Express the Line in Slope-Intercept Form
Line Graph:
Steps to Find Slope-Intercept Form
Line Graph:
Steps to Find Slope-Intercept Form
On this page:
- Calculator
- How to Find Slope-Intercept Form
- What is Slope-Intercept Form
- Slope-Intercept Form Equation
- Deriving the Equation
- Steps to Find the Equation of a Line
- Slope-Intercept Form for a Horizontal Line
- Slope-Intercept Form for a Vertical Line
- How to Find Slope-Intercept Form for Two Points
- How to Graph Slope-Intercept Form
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
Ethan has a PhD in astrophysics and is currently a satellite imaging scientist. He specializes in math, science, and astrophysics.
How to Find Slope-Intercept Form
There are several ways to describe a line using its slope, or gradient. The most commonly used method is an algebraic equation in slope-intercept form.
You can use a calculator like the one above to find the equation for a straight line in slope-intercept form, but you can also follow the steps below to find it.
Slope-intercept form is probably the most frequently used equation format to represent a line, but you can also express the line in point-slope form or standard form.
What is Slope-Intercept Form
Slope-intercept form is a type of linear equation format used to express a straight line. The slope-intercept form equation can be used to find any point on the line.
Slope-intercept form gets its name because the equation contains the slope and the y-intercept of the line. The combination of these elements can be used to plot any point on the line.
Slope-intercept form is applicable when you have the slope and y-intercept for a line or when you can calculate these for the line. The y-intercept is the y-coordinate where the line crosses the y-axis.
Slope-Intercept Form Equation
The slope-intercept form equation is given by:
y = mx + b
The slope-intercept form of a line states that the y-coordinate y of a point on the line is equal to the slope m times the x-coordinate x plus the y-intercept b.
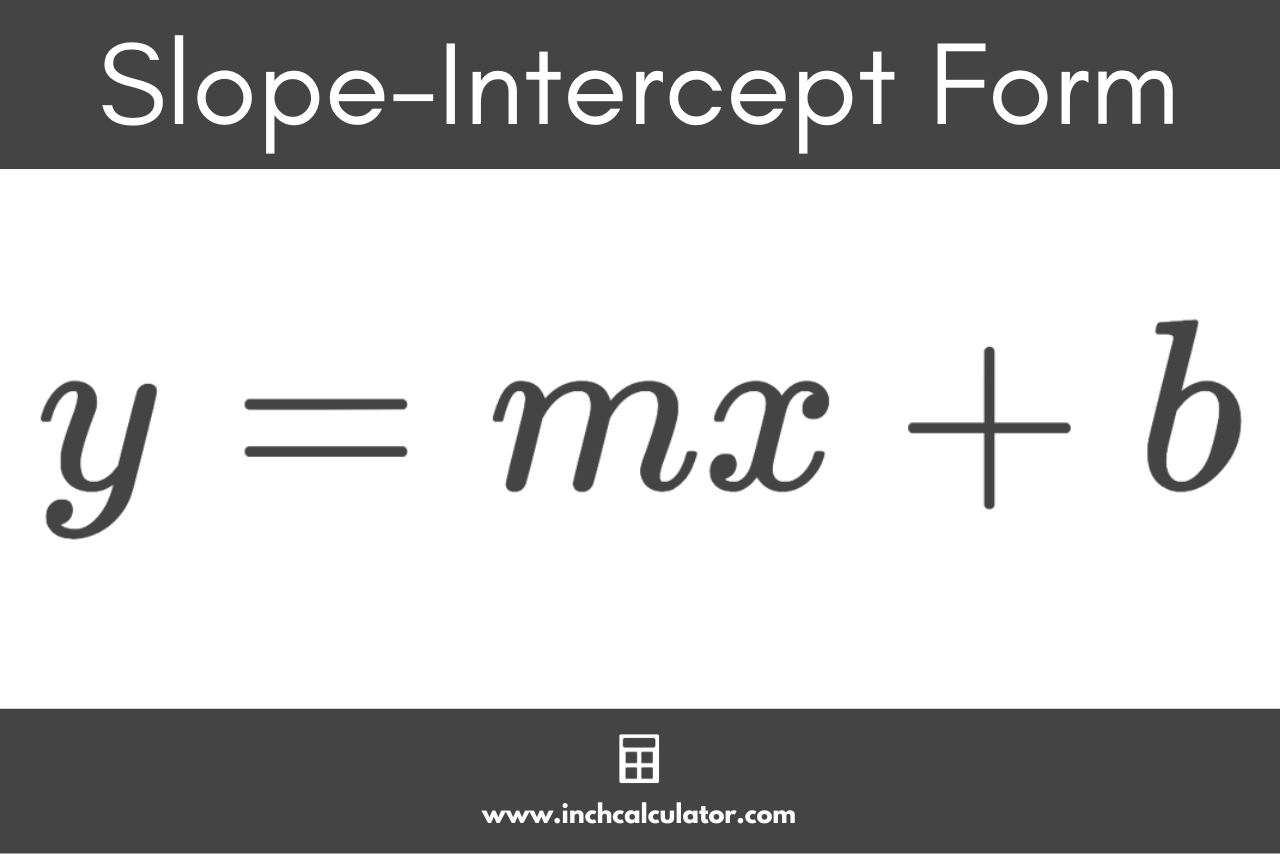
In the slope-intercept formula, the slope of the line m is the coefficient for the x-coordinate, and the y-intercept is represented as the b variable.
Deriving the Equation
Slope-intercept form is derived from the slope formula.
The formula for slope using the coordinates for two points (x1, y1) and (x2, y2) is:
m = (y2 – y1) / (x2 – x1)
If you multiply both sides of this equation by the denominator (x2 – x1), the formula can be rewritten as:
m × (x2 – x1) = (y2 – y1) / (x2 – x1) × (x2 – x1)
m(x2 – x1) = y2 – y1
Now, we can substitute the y-intercept (which, by definition, is the coordinate (0, b)) for (x1, y1).
m(x2 – 0) = y2 – b
m(x2) = y2 – b
Rearranging, we get:
y2 = m(x2) + b
Then, since point (x2, y2) is an arbitrary point on the line, we can rename it to just (x, y).
y = mx + b
Finally, we see that the resulting equation of the line is the slope-intercept form equation above.
Steps to Find the Equation of a Line
You can express the equation of a straight line in slope-intercept form in a few steps.
Step One: Find the Slope
The first step is to find the line’s slope. If you know two points on the line, you can use the slope formula above to find it or use a slope calculator.
If you know the slope already, then you can skip this step.
Step Two: Find the Y-Intercept
Input the slope and coordinates for a known point on the line for the m, x, and y variables, respectively, in the slope-intercept form equation. Then, solve for b.
y = mx + b
y – mx = mx + b – mx
b = y – mx
You can also find b using a y-intercept calculator.
Step Three: Express the Line in Slope-Intercept Form
Now, input the slope and y-intercept for the m and b variables in the slope-intercept form equation.
y = mx + b
The result is the equation of the line in slope-intercept form.
For example, let’s create the equation for a line with a slope of 1/2 and a point (5, 6) in slope-intercept form.
Since we know the slope, we can start with the second step and input 1/2 for the m variable, 5 for the x variable, and 6 for the y variable to solve for b using slope-intercept form.
6 = (1 / 2 × 5) + b
6 = 5 / 2 + b
6 – 5 / 2 = 5 / 2 + b – 5 / 2
b = 7 / 2
Then, express the line in slope-intercept form using the slope of 1/2 and the y-intercept of 7/2.
y = 1 / 2x + 7 / 2
Slope-Intercept Form for a Horizontal Line
You can also use slope-intercept form to express a horizontal line. A horizontal line runs parallel to the x-axis and has a slope of 0, meaning it has no steepness at all.
So, let’s substitute 0 for m in the slope-intercept form equation.
y = 0x + b
If you simplify this to remove the 0x portion, the result is:
y = b
And that’s the equation of a horizontal line in slope-intercept form. The y-coordinate is always equal to the y-intercept.
Slope-Intercept Form for a Vertical Line
A vertical line is a line that runs parallel to the y-axis, and since it has infinite steepness, the slope is undefined. Since vertical lines have an undefined slope, they cannot be represented using slope-intercept form.
But, a vertical line is commonly expressed as x = c, where c is the x-intercept and also x-coordinate of any point on the line.
x = c
How to Find Slope-Intercept Form for Two Points
If you have two points on a line, then you can also find the slope-intercept form.
The first step to do this is to find the slope using the slope formula we showed above.
m = (y2 – y1) / (x2 – x1)
Substitute the coordinates (x1, y1) and (x2, y2) for the two points in the slope formula, then solve for m.
After you have solved for m, you can use it along with one of the points to find the y-intercept and put the equation of the line in slope-intercept form following the steps above.
How to Graph Slope-Intercept Form
To graph a line with an equation in slope-intercept form, start by finding one point and slope from the equation.
Remember that slope-intercept form looks like this:
y = mx + b
When you have the equation of a line in this form, you can start by getting the slope m in the equation. The slope is the coefficient of the x-coordinate in the equation.
As we noted above, the b variable represents the y-intercept. That means that if you get the b variable from the equation, you know the point has an x-coordinate of 0.
Thus, one known point on the line is (0, b).
Next, you need to find a second point on the line using the slope and the first point. The slope is the ratio of a line’s vertical change to horizontal change, and you can use that ratio to find a second point from the first one.
Given the point (0, b), the second point is equal to (slope denominator + 0, slope numerator + b).
Then, you can draw the first and second points on the graph and connect them with a straight line and extend that line indefinitely to the right and left of the points.
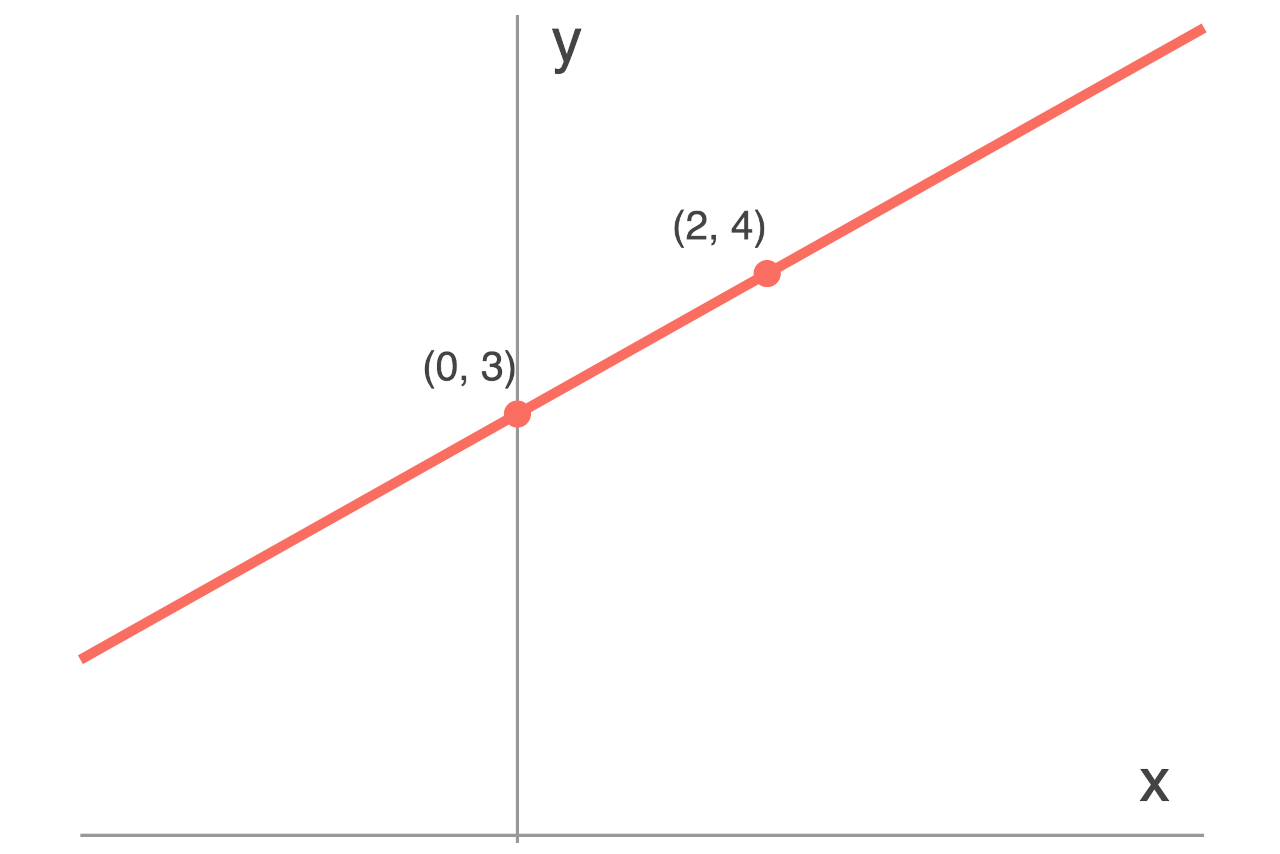
For example, let’s find the two points to graph a line from the equation y = 1/2x + 3.
Start by finding the slope. In this equation, m equals 1/2, so that’s the slope.
Then find the coordinates for the first point. In the equation above, b is equal to 3. So, the first point is (0, 3).
Now you can use the slope and first point to find a second point on the line. Add the slope’s denominator 2 to the first point’s x-coordinate. Since the x-coordinate is 0, the x-coordinate of the second point is just the slope’s denominator.
2 + 0 = 2
Then add the slope’s numerator to the first point’s y-coordinate, which is the y-intercept.
1 + 3 = 4
Put these together to find the second point, which is (2, 4).
And finally, you can plot the points (0, 3) and (2, 4) on a graph and connect them to graph the line.
