Equation of a Line Calculator
Express the equation of a line in standard form, slope-intercept form, and point-slope form using the calculator below. You can use two known points, the slope and one known point on the line, or the slope and y-intercept.
Line Equations:
Standard Form:
Slope-Intercept Form:
Point-Slope Form:
Line Graph:
Standard Form:
Slope-Intercept Form:
Point-Slope Form:
Line Graph:
Standard Form:
Slope-Intercept Form:
Point-Slope Form:
Line Graph:
On this page:
- Calculator
- How to Find the Equation of a Line
- Three Main Forms of Linear Equations
- Standard Form Equation
- Slope-Intercept Form Equation
- Find Point-Slope Form Equation
- How to Find a Linear Equation Using One Point and the Slope
- How to Find a Line Equation Using Two Points
- Equation of a Horizontal Line
- Equation of a Vertical Line
- References
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
Ethan has a PhD in astrophysics and is currently a satellite imaging scientist. He specializes in math, science, and astrophysics.
How to Find the Equation of a Line
When working with lines, it’s possible to express the line using an equation/function or by plotting on a graph. When expressing a line using an equation, the equation allows you to find the Cartesian coordinates for any point on the line, which you can use to plot it on a graph.
Equations can be used to mathematically express lines as well as curves. However, the calculator above allows you to find the equations for linear lines.
For lines, there are three commonly used forms for a linear equation that can all be used to describe the line using its slope.
Three Main Forms of Linear Equations
There are three different forms of a linear equation often used to express a line; they are standard form, slope-intercept form, and point-slope form. These are different ways to describe the same line using different equation formats created using a combination of coordinates for a point on the line and the slope of the line.
Keep reading, and we’ll cover each of these in more detail.
Standard Form Equation
Standard form is the standard format for linear equations. Standard form is a formula to express the equation of a line in a slightly different way than slope-intercept form and point-slope form, which are both covered below.
The standard form line equation is:[1]
Ax + By = C
The standard form equation for a linear line states that A times the x-coordinate is equal to B times the y-coordinate equals the y-intercept C.
To use standard form, the values for each coefficient, A and B, must be a whole number since decimals are generally not used in standard practice. Additionally, in standard practice, the coefficient for A must also be positive.
In addition to the rules above, the equation should be simplified such that coefficients A, B, and C do not have any common factors other than 1.
A and B are the coefficients for the x and y coordinates of a point, and C is the y-intercept where the line crosses the y-axis.
If there are any fractions in the equation, then multiply both sides by the denominator of the fractions to remove them.
This is the standard form for linear equations, but there are also other ways to express the equation of a line.
Slope-Intercept Form Equation
Slope-intercept form is one of the most frequently used equations to represent a line. To use slope-intercept form, you need the slope and the y-intercept of the line.
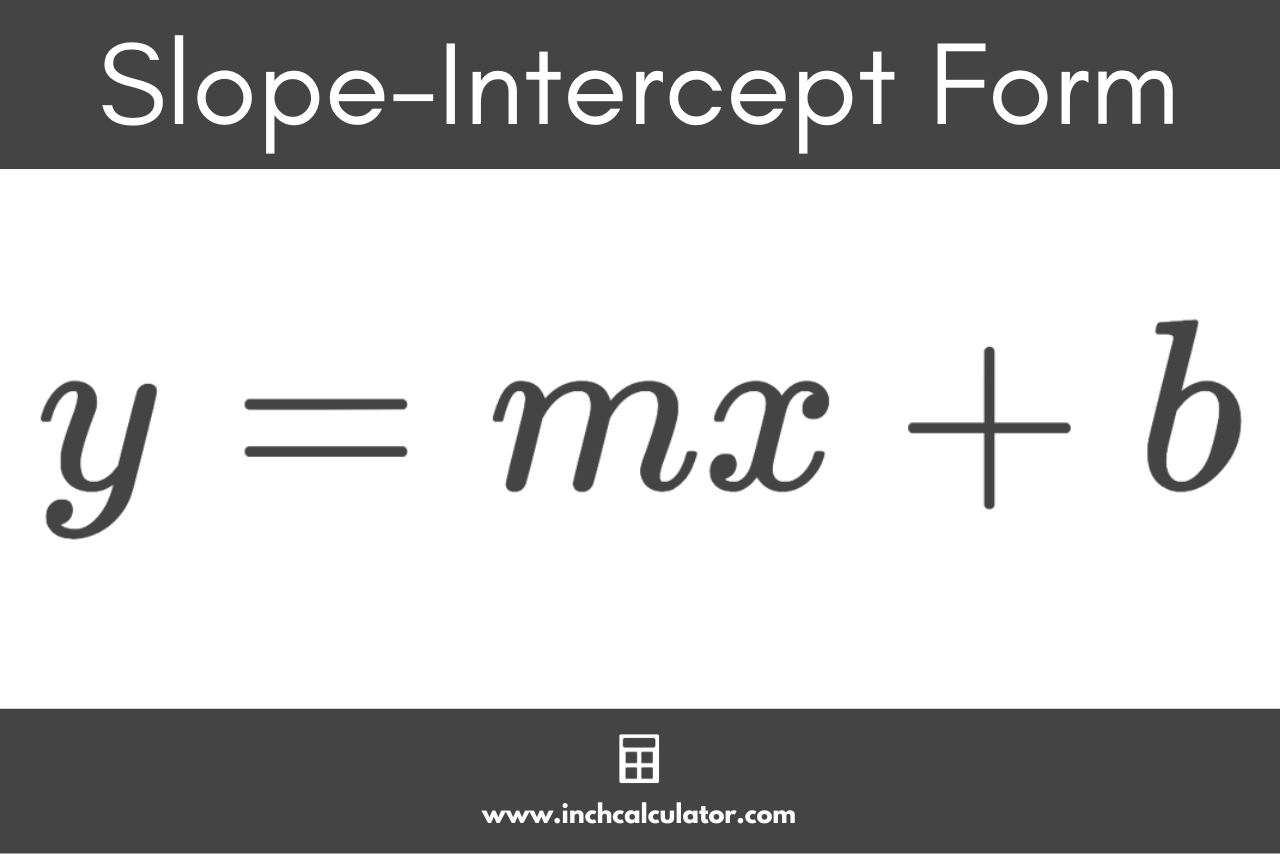
The slope-intercept form equation is given by:[2]
y = mx + b
The slope-intercept form equation for a line states that the y-coordinate of a point on the line is equal to the x-coordinate of the point x times the slope m, plus the y-intercept b.
Find Point-Slope Form Equation
Point-slope form is another form of equation to express a linear line. To use point-slope form, you need the slope and one point on the line.
The point-slope form equation is:[3]
y – y1 = m(x – x1)
The point-slope form equation states that y minus y1 is equal to the slope of the line m times x minus x1. In other words, the difference in y coordinates between two points is equal to the slope times the difference in the x coordinates of those two points.
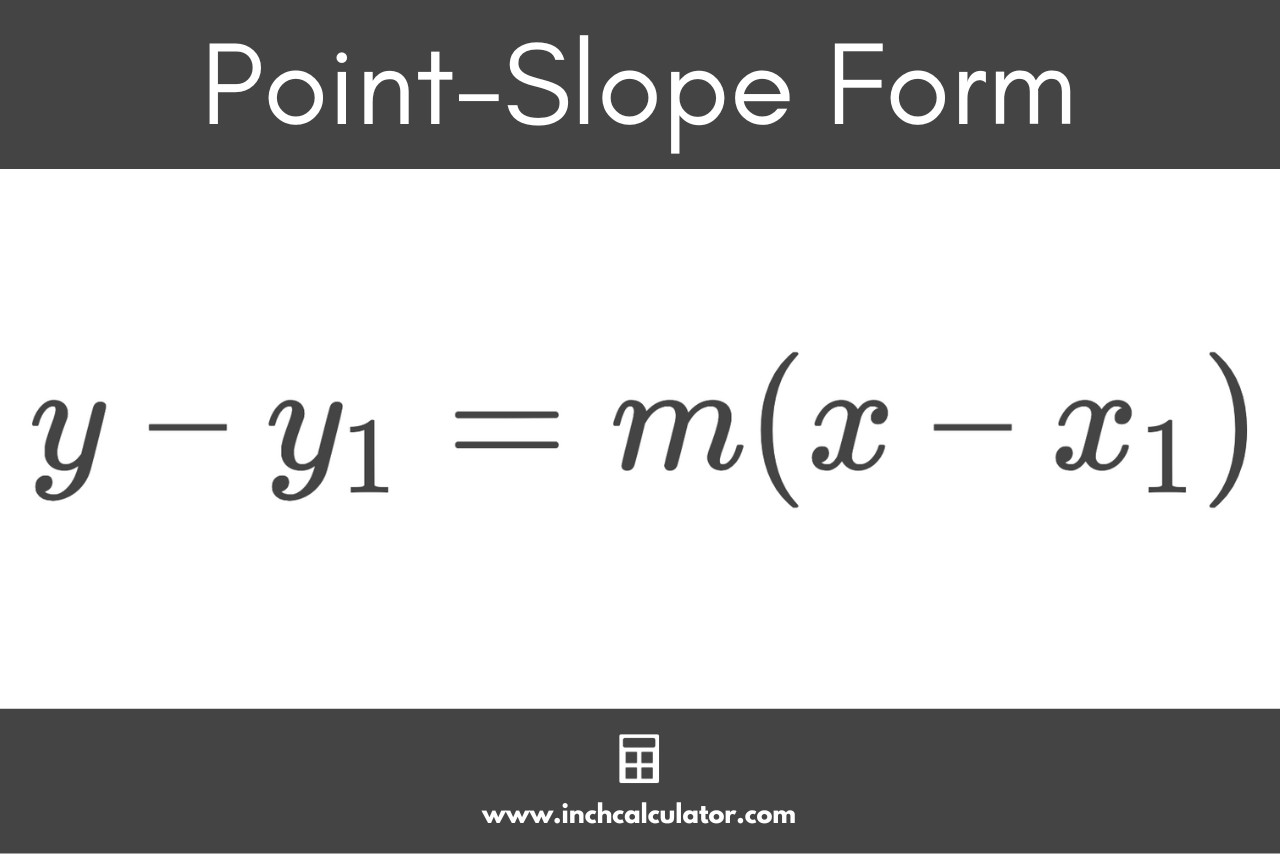
How to Find a Linear Equation Using One Point and the Slope
You can write the equation of a straight line in a few steps if you know the slope and have the coordinates of one point on the line.
Step One: Find the Y-Intercept of the Line
If you input the slope and x & y coordinates for the known point for the m, x, and y variables in the slope-intercept form equation, you can solve for the y-intercept b.
y = mx + b
y – mx = mx + b – mx
b = y – mx
You can also use a y-intercept calculator to find the y-intercept.
Step Two: Express the Line as an Equation
Finally, substitute the slope and y-intercept for the m and b variables in the slope-intercept form equation, respectively.
y = mx + b
The resulting equation is the slope-intercept form equation for the line.
How to Find a Line Equation Using Two Points
If you know two points on the line, then you can also express the line as an equation.
The first step to do this is to find the slope using the slope formula:
m = (y2 – y1) / (x2 – x1)
The slope formula states that m is equal to y2 minus y1 divided by x2 minus x1. In other words, the slope is equal to the vertical change of the line divided by the horizontal change.
Input the coordinates for the two points in the slope formula, then solve for m.
After you have solved for the slope, you can use it along with one of the points to find the y-intercept and express the equation of the line in slope-intercept form by following steps one and two above.
Equation of a Horizontal Line
When the line is a horizontal line that is parallel to the x-axis (0° angle to the x-axis), it has a slope equal to 0.
When you substitute 0 for m in the slope-intercept form equation, the result looks like this:
y = 0x + b
This can be simplified to:
y = b
So, the equation of a horizontal line states that for any value of x, the y-coordinate is always equal to the y-intercept b, or the y-coordinate of any other point on the line.
Equation of a Vertical Line
When the line is a vertical line that is perpendicular to the x-axis (90° angle to the x-axis), the slope is undefined. When the slope is undefined, slope-intercept form and point-slope form cannot be used to express the equation of the line.
The standard form equation for a vertical line is:
1x + 0y = C
This can be simplified to:
x = C
So, in the case of a vertical line, for any y-coordinate, x is equal to a constant C, where C is equal to the x-coordinate for any point on the line.
References
- IXL, Standard form of linear equations, https://www.ixl.com/math/lessons/standard-form-of-linear-equations
- CK-12 Foundation, Linear Equations in Slope-Intercept Form, https://www.ck12.org/book/ck-12-algebra-basic/section/5.1/
- Clapham, C., Nicholson, J., Oxford Concise Dictionary of Mathematics, 475. https://web.archive.org/web/20131029203826/http://web.cortland.edu/matresearch/OxfordDictionaryMathematics.pdf