Unit Circle Calculator
Calculate the coordinates for a point on the unit circle given the central angle in radians or degrees. You’ll also get the sine, cosine, and tangent in the results.
Solution:
x = cos(θ)
y = sin(θ)
tan(θ)
On this page:
- Calculator
- What is the Unit Circle
- How to Find Coordinates on the Unit Circle
- Unit Circle Chart with Radians and Degrees
- Unit Circle Chart
- Tricks to Remember the Unit Circle
- Degree to Radian Conversions
- Trig Functions for Common Angles
- Memorize the Four Quadrants
- Memorize the Key Properties of the Four Quadrants
- Memorize the Three Core Trigonometry Functions
- Frequently Asked Questions
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
Ethan has a PhD in astrophysics and is currently a satellite imaging scientist. He specializes in math, science, and astrophysics.
What is the Unit Circle
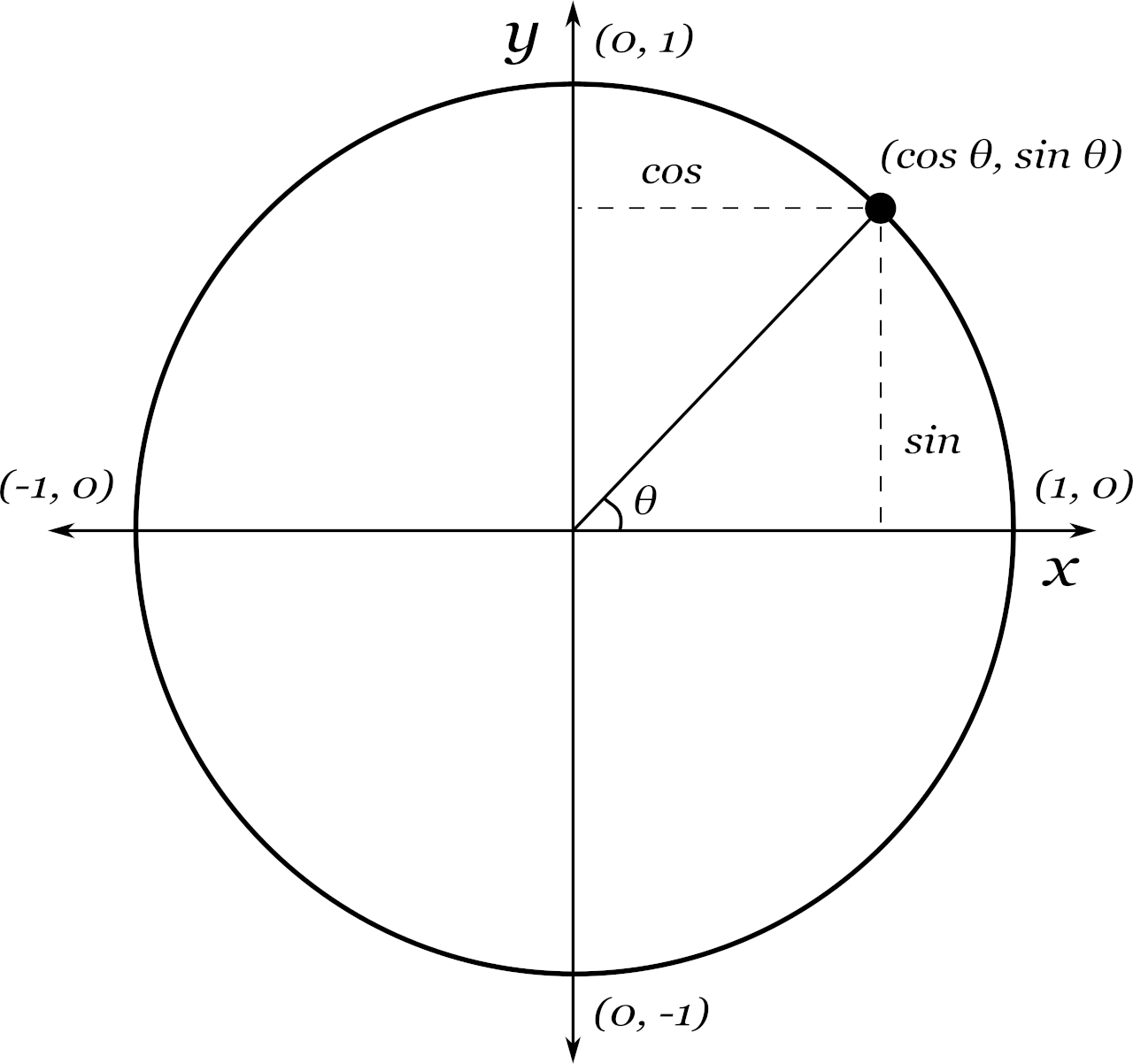
The unit circle is a circle with a radius equal to 1 and is centered at the origin. It is sometimes also referred to as the trig circle because it’s used to calculate the cosine, sine, and tangent of any angle within the circle.
The unit circle defines how to find the length of the sides of a right triangle formed when extending a line from the origin to the edge of the circle for a known angle.
Since the radius of the unit circle is 1, the length of the right triangle’s hypotenuse is equal to 1.
As seen in the image above, the height of the triangle (leg a) is equal to the sine of the angle, while the length of the base of the triangle (leg b) is equal to the cosine.
How to Find Coordinates on the Unit Circle
For a specified angle, the point, or coordinate, where the radius intersects the circle can be calculated using trigonometric functions.
As noted above, the height of the right triangle formed is equal to the sine of the angle θ; this becomes the y-coordinate. The length of the base of the triangle is equal to the cosine of the angle, which becomes the x-coordinate.
Thus, the coordinate where the radius intersects the circle is:
(cos θ, sin θ)
Unit Circle Chart with Radians and Degrees
The unit circle chart shows the angles used in the 30-60-90 and 45-45-90 special right triangles, and the coordinates where the radius intersects the edge of the unit circle.
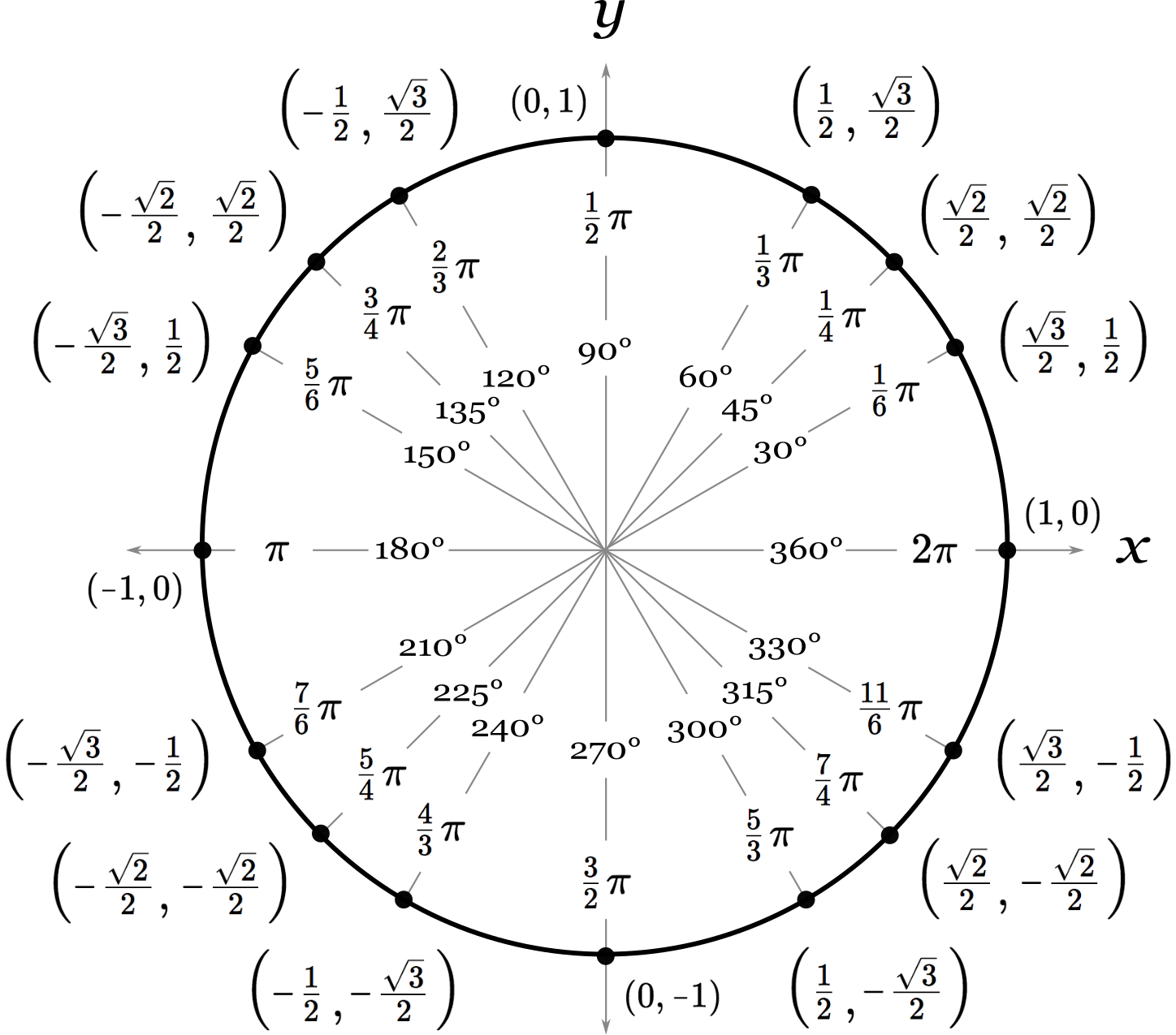
The chart shows the angles in radians and degrees, and shows each coordinate solved using the special right triangle created using the unit circle.
Note that the unit circle repeats after 360 degrees or 2π radians. Therefore, when using the unit circle with an angle greater than 360 degrees/2π radians, you should subtract 360 degrees/2π radians repeatedly until the angle is between 0 and 360 degrees/2π radians.
Unit Circle Chart
| Angle (degrees) | Angle (radians) | Unit Circle Coordinates |
|---|---|---|
| 30° | π / 6 | (√3 / 2, 1 / 2) |
| 45° | π / 4 | (√2 / 2, √2 / 2) |
| 60° | π / 3 | (1 / 2, √3 / 2) |
| 90° | π / 2 | (0, 1) |
| 120° | 2π / 3 | (-1 / 2, √3 / 2) |
| 135° | 3π / 4 | (-√2 / 2, √2 / 2) |
| 150° | 5π / 6 | (-√3 / 2, 1 / 2) |
| 180° | π | (-1, 0) |
| 210° | 7π / 6 | (-√3 / 2, –1 / 2) |
| 225° | 5π / 4 | (-√2 / 2, –√2 / 2) |
| 240° | 4π / 3 | (-1 / 2, –√3 / 2) |
| 270° | 3π / 2 | (0, -1) |
| 300° | 5π / 3 | (1 / 2, –√3 / 2) |
| 315° | 7π / 4 | (√2 / 2, –√2 / 2) |
| 330° | 11π / 6 | (√3 / 2, –1 / 2) |
| 360° | 2π | (1, 0) |
Tricks to Remember the Unit Circle
The unit circle might intimidate you, but remembering it might be easier than it might seem at first glance. There are a few tricks you can use to memorize the unit circle.
Try these tricks to memorize the unit circle without needing to remember every coordinate.
Degree to Radian Conversions
The following table shows degree to radian conversions for the angles in the unit circle.
| Degrees | Radians |
|---|---|
| 30° | π / 6 |
| 45° | π / 4 |
| 60° | π / 3 |
| 90° | π / 2 |
| 120° | 2π / 3 |
| 135° | 3π / 4 |
| 150° | 5π / 6 |
| 180° | π |
| 210° | 7π / 6 |
| 225° | 5π / 4 |
| 240° | 4π / 3 |
| 270° | 3π / 2 |
| 300° | 5π / 3 |
| 315° | 7π / 4 |
| 330° | 11π / 6 |
| 360° | 2π |
Trig Functions for Common Angles
The following table shows common angles and the resulting values using the trig functions for the top right quadrant of the unit circle. You’ll notice these coordinates and their negative values repeated for the entire unit circle.
| Angle (θ) | Trig Functions | ||
|---|---|---|---|
| degrees | radians | sin θ | cos θ |
| 30° | π / 6 | 1 / 2 | √3 / 2 |
| 45° | π / 4 | √2 / 2 | √2 / 2 |
| 60° | π / 3 | √3 / 2 | 1 / 2 |
Memorize the Four Quadrants
You may notice there is fantastic symmetry on the unit circle. The circle is divided into four quadrants, each separated by a right angle, or 90 degrees.
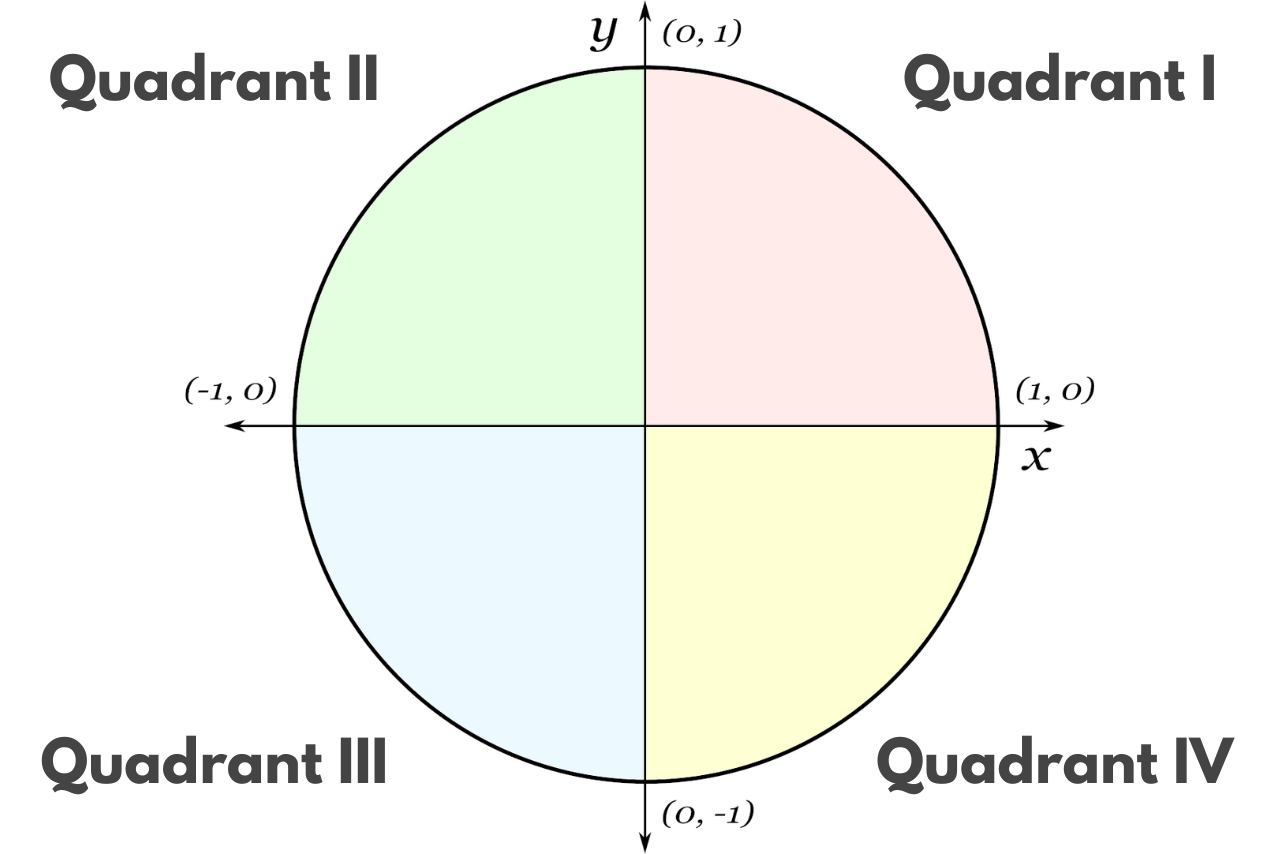
At each of the lines dividing the quadrants, one of the trig functions equals zero, and the other equals either 1 or -1. Memorize the coordinates of these four points.
Each quadrant is then divided into three sections, one 30 degrees, one 45 degrees, and one 60 degrees from the previous quadrant divider. For example, the third quadrant begins at 180 degrees, so the three key angles are:
- 180 + 30 = 210 degrees
- 180 + 45 = 225 degrees
- 180 + 60 = 240 degrees
Finally, and this is the toughest part, it’s important to memorize the x and y coordinates (or (cos θ, sin θ) values) of the 30, 45, and 60-degree angles in the first quadrant. If you can do this, you can easily find the values for the rest of the important angles on the unit circle.
Memorize the Key Properties of the Four Quadrants
Once you know the coordinates of the four quadrant dividers (which are (1,0), (0, 1), (-1, 0), (0, -1) when moving counter-clockwise beginning with the positive x-axis) as well as the coordinates of the quadrant 1 important angles (30, 45, 60 degrees), then you can apply these to the other three quadrants.
The coordinates of the special angles are the same in all quadrants, except sometimes the sine values are negative, sometimes the cosine values are negative, and sometimes both are negative.
To figure out which values are positive, remember the phrase “All Students Take Courses”. This is a handy mnemonic device for the words “all”, “sine”, “tangent”, and “cosine”, where “all” applies to quadrant 1, “sine” to 2, “tangent” to 3, and “cosine” to 4.
What these words indicate are which values are positive in their respective quadrants.
- Quadrant 1: all coordinates are positive
- Quadrant 2: only sine values are positive
- Quadrant 3: only tangent values are positive
- Quadrant 4: only cosine values are positive
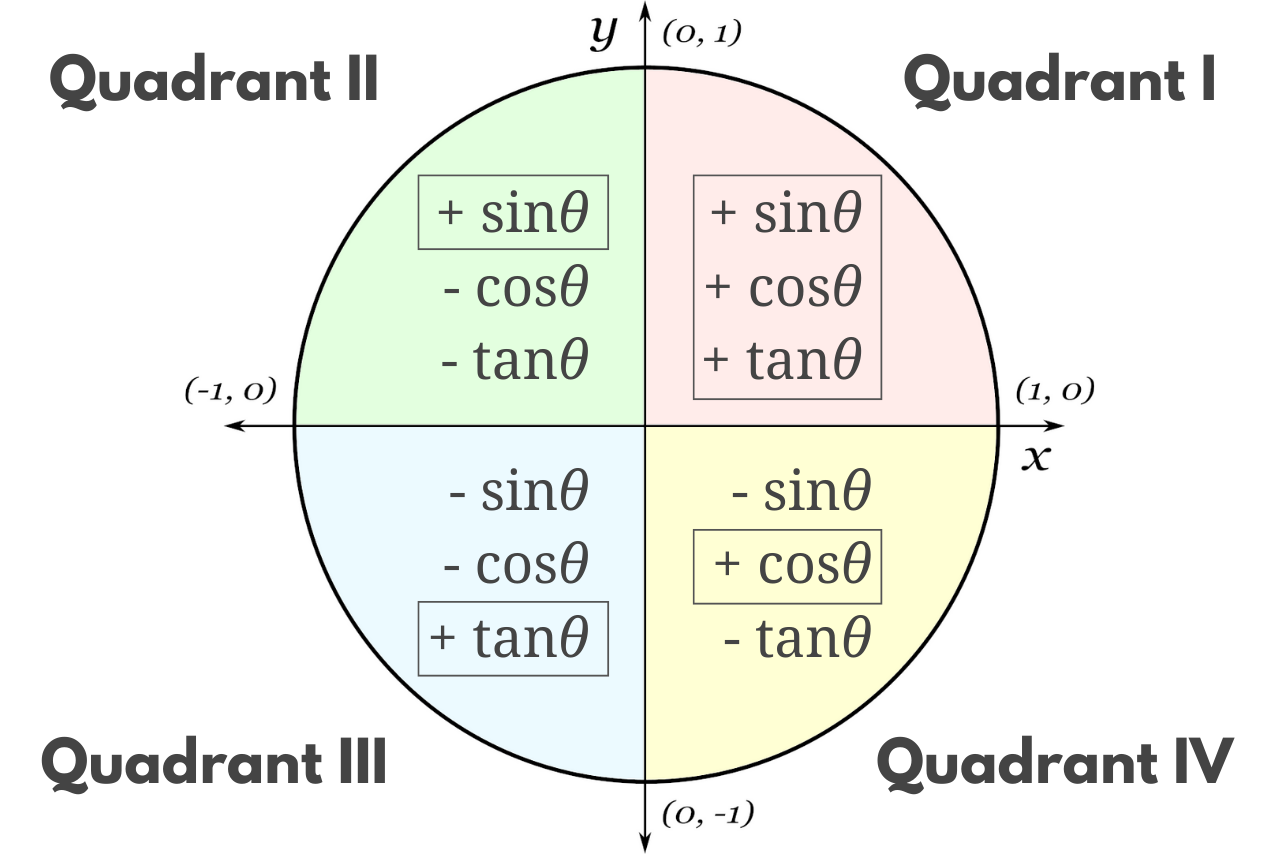
Putting this all together in an example, let’s say you want to find the coordinates of the angle 315 degrees. The previous quadrant divider is at 270 degrees, so if we subtract 270 from 315 we have 45 degrees.
Therefore, we know from the first quadrant that the (x, y) coordinates are going to be some variation of (√2/2, √2/2). Since we are in the fourth quadrant and we remember “All Students Take Courses”, we know that only Cosine values are positive in quadrant 4.
So we must set the sine value to be negative, and we find the coordinates for a 315-degree angle are (√2/2, -√2/2).
Memorize the Three Core Trigonometry Functions
The three key trigonometry functions applied to an angle are cosine, sine, and tangent. These are the three functions that we apply to find the coordinates of a given angle on the unit circle. Using all the information above, you will be able to find the cosine and sine values of the important angles.
To find the tangent of the angle, divide the sine value by the cosine value. That is:
tan θ = sin θ / cos θ
Remember these tips, and you will master the unit circle in no time!
Frequently Asked Questions
Why is the unit circle important?
The unit circle is important because it allows us to calculate the cosine, sine, and tangent of an angle less than 360 degrees or 2π with ease.
Can you use degrees on the unit circle instead of radians?
Yes! Both degrees and radians are equally useful units to use to measure angles on the unit circle.
What is the radius of the unit circle?
By definition, the unit circle has a radius of 1.
How do you find the tangent of an angle using the unit circle?
To find the tangent of an angle on the unit circle, simply find the sine and cosine values of the angle and then divide the sine value by the cosine value. That is, we can calculate the tangent of an angle, θ, by doing
tan θ = sin θ / cos θ