Pentagon Calculator

Calculate any part of a pentagon using the pentagon calculator below.

diagram of a pentagon showing the sides, diagonal, height, circumradius, and apothem

Have a Question or Feedback?

Solution:

Side (a):	3
Area (A):	15.484
Perimeter (P):	15
Diagonal (d):	4.854
Height (h):	4.617
Circumradius (R):	2.552
Inradius (r):	2.065

Learn how we calculated this below

scroll down

Add this calculator to your site

How to Calculate the Properties of a Pentagon

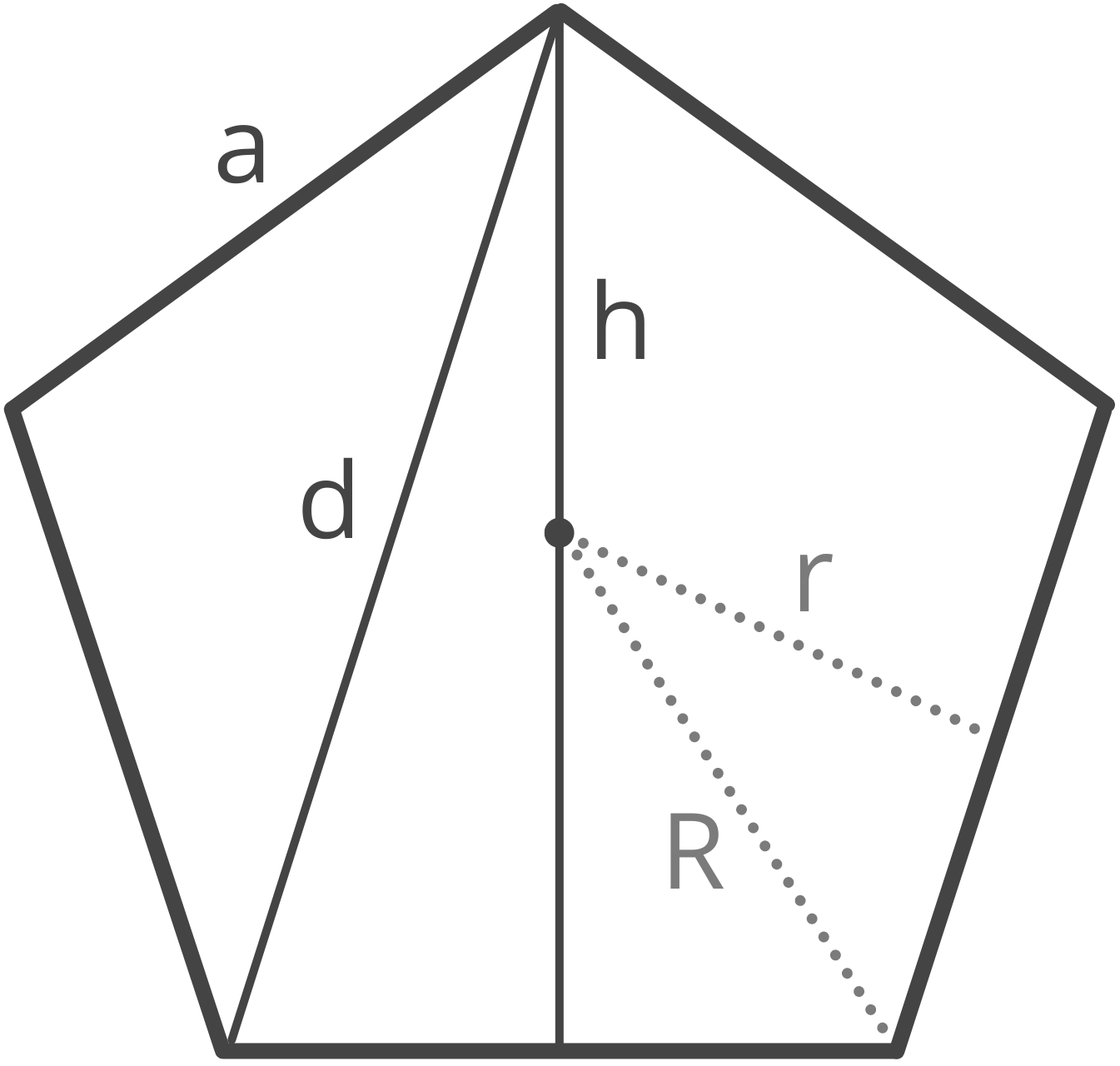
A pentagon is a two-dimensional geometric shape with five straight sides. The properties of a pentagon include the length of the sides a, the area A, the perimeter P, the diagonal d, the height h, the radius (circumradius) R, and apothem (inradius) r.

A pentagon is a polygon with five sides and five angles. When all its sides and angles are equal, it’s referred to as a ‘regular’ pentagon. A regular pentagon is symmetric, with all its internal angles measuring 108 degrees. It can be divided into five isosceles triangles of equal size.

Graphic showing that a regular pentagon is composed of five isosceles triangles.

How to Calculate the Area of a Pentagon

To find the area of a regular pentagon, you can use the pentagon area formula:

A = \frac{1}{4} \sqrt{5 \left ( 5 + 2 \sqrt{5} \right ) } \times a^{2}

The area A of a pentagon is equal to 1/4 times the square root of 5 times 5 plus 2 times the square root of 5, times the length of the sides a squared.

Graphic showing the formula to calculate the area of a pentagon.

How to Calculate the Perimeter of a Pentagon

Since a regular pentagon has five equal sides, to find the perimeter, you can multiply the length of the sides by 5.

P = 5a

The perimeter P of a pentagon is equal to 5 times the length of the sides a.

How to Calculate the Diagonal of a Pentagon

In a regular pentagon, the diagonal connects two non-adjacent vertices.

You can calculate the length of the diagonal using a formula:

d = \frac{1 + \sqrt{5}}{2} \times a

The diagonal d of a pentagon is equal to 1 plus the square root of 5, divided by 2, times the side length a.

How to Calculate the Height of a Pentagon

In a regular pentagon, the height extends from the center of one of the sides to the opposite vertex.

You can calculate the height of the pentagon using a formula:

h = \frac{\sqrt{5 + 2 \sqrt{5}}}{2} \times a

The height h is equal to the square root of 5 plus 2 times the square root of 5, divided by 2, times the side length a.

How to Calculate the Circumradius and Inradius of a Pentagon

Just like a hexagon or an octagon, a pentagon has a circumradius and an inradius.

The circumradius of a pentagon is the radius of the circumscribed circle that passes through all the vertices of the pentagon. The circumradius is often referred to as just the radius.

The inradius, or the apothem, of a pentagon is the perpendicular distance from the center of the pentagon to one of its sides. In a regular pentagon, this is also the height of one of the isosceles triangles when split.

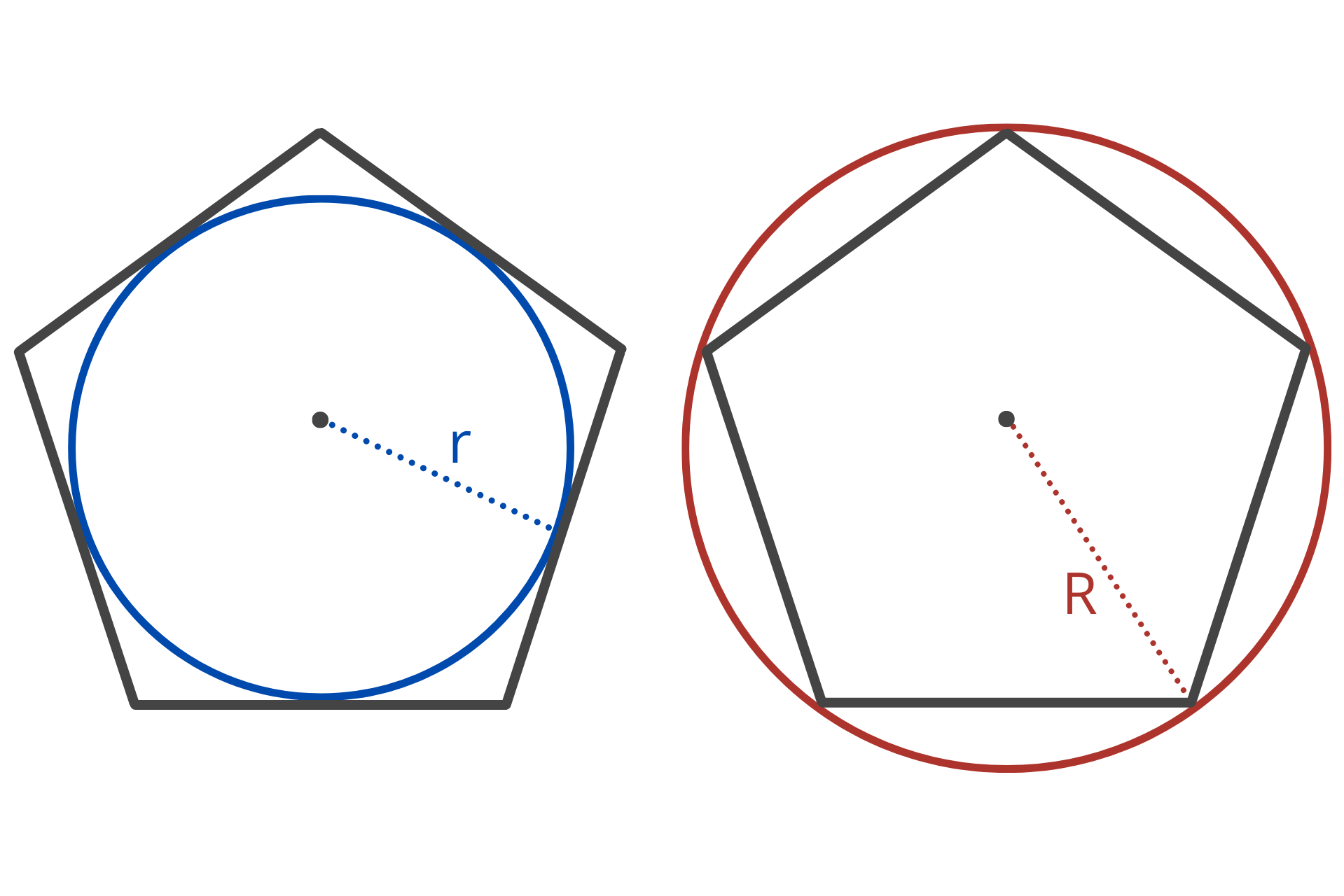
Graphic showing the circumradius and inradius of a pentagon.

You can calculate the circumradius and apothem using a few formulas.

Circumradius (Radius)

The formula to calculate the circumradius of a pentagon is:

R = \frac{\sqrt{50 + 10 \sqrt{5}}}{10} \times a

The circumradius R is equal to the square root of 50 plus 10 times the square root of 5, divided by 10, times the side length a.

Inradius (Apothem)

The formula to calculate the apothem of a pentagon is:

r = \frac{\sqrt{25 + 10 \sqrt{5}}}{10} \times a

The apothem r is equal to the square root of 25 plus 10 times the square root of 5, divided by 10, times the side length a.