Sector Area Calculator
Calculate the area of a sector using the central angle and radius below and learn the formula and steps to solve it below.
Results:
Sector Area (A)
Arc Length (s)
Chord Length (a)
On this page:
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
Ethan has a PhD in astrophysics and is currently a satellite imaging scientist. He specializes in math, science, and astrophysics.
How to Calculate Sector Area
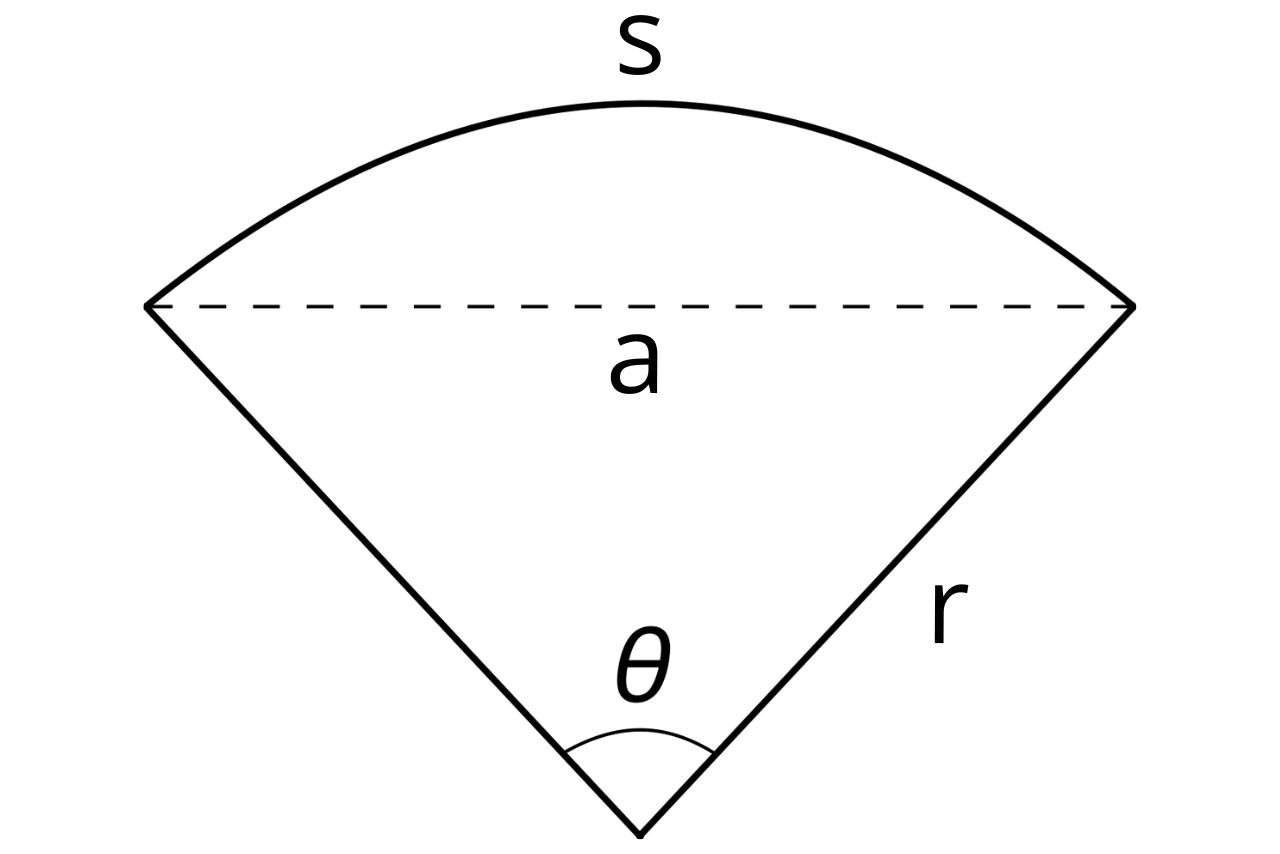
A sector is a pie-slice-shaped portion of a circle where its straight edges are two radii of the circle, and the outer curve portion of the circle’s outer arc. A defining characteristic of a sector is its central angle, denoted as θ (Greek letter theta).
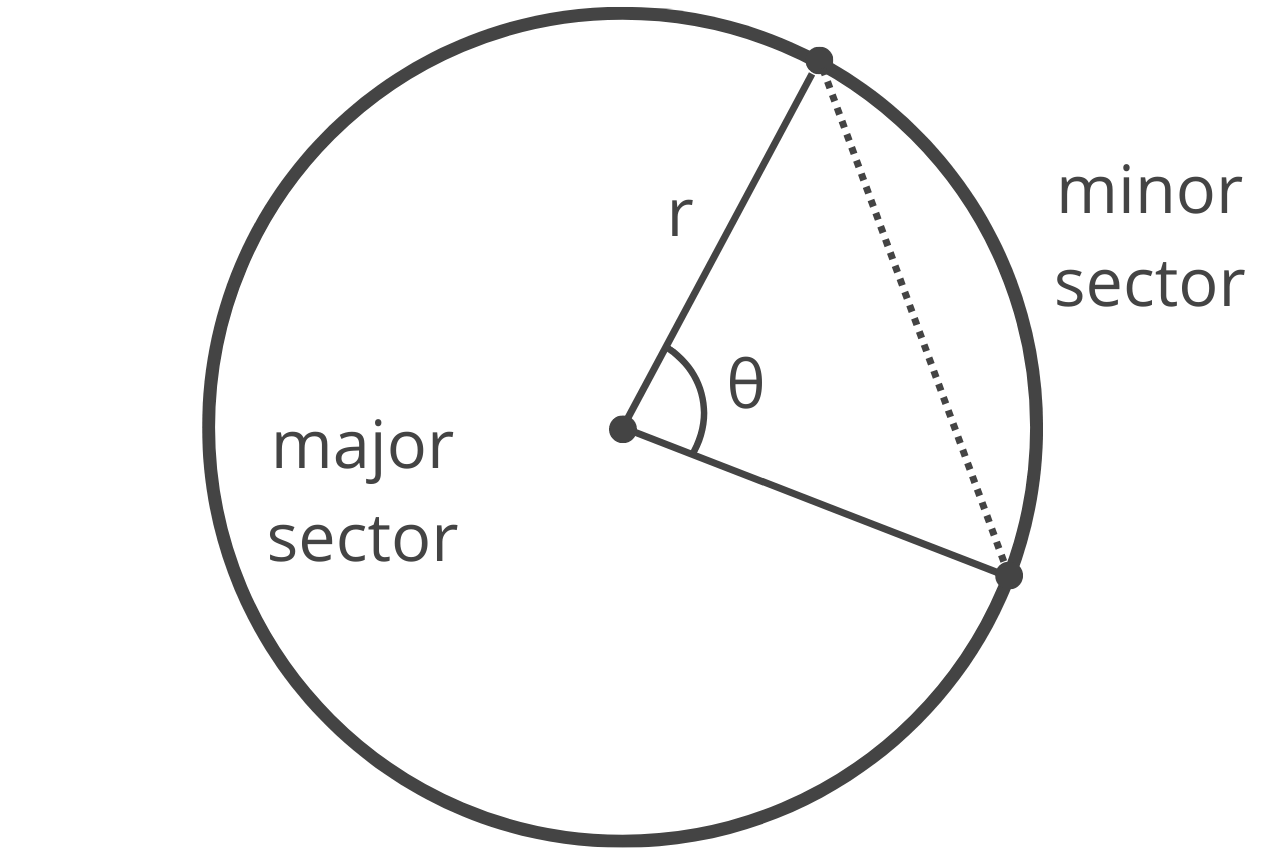
If the central angle is greater than 180°, then it is considered a major sector of the circle, and if the central angle is less than 180°, it is a minor sector. If the central angle is exactly equal to 180°, then it is a semi-circle.
Another characteristic of a sector is the chord, which is the line that connects the two points where the radii intersect the arc. The chord subdivides a sector into a triangle and a segment.
To calculate the area of a sector, a simple formula can be used.
Sector Area Formula
The area of a sector can be found using the formula:
sector area = 1 / 2r²θ
Thus, a sector’s area is equal to the radius r squared times the central angle θ in radians, divided by 2. If you know the diameter of the circle, you can find the radius by dividing the diameter in half.
Note that to use this formula, the central angle must be in radians. You can use our degrees to radians converter to convert to radians if needed.
For example, find the area of a sector with a radius of 12 and a central angle of 1.5 radians.
area = 1 / 2 × 12² × 1.5
area = 1 / 2 × 144 × 1.5
area = 1 / 2 × 216
area = 108
Thus, the area of the sector is 108.
Sector Area Using Degrees
If you know the central angle in degrees, then the formula to find the area of a sector is a little different:
sector area = θ / 360 × πr²
The area is equal to the central angle θ in degrees divided by 360, times pi times the radius squared.
This formula is derived from the formula to find the area of a circle, which states that the area of a circle is equal to πr². Since the central angle of an entire circle is equal to 360° and a sector is a portion of the circle, the θ/360 finds the fraction of the full circle area represented by the sector.
So essentially, we are calculating the area of the full circle and then taking just a fraction of it.
For example, find the area of a sector with a radius of 7 and a central angle of 40 degrees.
area = 40 / 360 × π× 7²
area = 1 / 9 × π× 49
area = 17.104
Therefore, the area of the sector is equal to 17.104.
Semi-Circle Area Formula
A semi-circle is a special type of sector equal to exactly half of a circle. The central angle of a semi-circle is 180°, or π radians.
The formula to find the area of a semi-circle is:
semi-circle area = πr² / 2
The area is equal to pi times the radius squared, divided by 2.
Quadrant Area Formula
A quadrant is another special type of sector equal to exactly one-quarter of a circle. The central angle of a quadrant is 45°.
The formula to find the area of a quadrant is:
quadrant area = πr² / 4
The area is equal to pi times the radius squared, divided by 4.
You might also find our arc length calculator useful for solving the arc length of a sector.
Frequently Asked Questions
Is a sector the same as an arc?
No, a sector is a pizza-slice-shaped fraction of a circle, whereas an arc is the curved outer portion of the sector. An arc has units of length, while a sector is an area with units of length squared.
How do you find the area of a sector with a known arc length?
If you know the arc length of a sector and want to find its area, you must also know its radius. You can then solve for the central angle θ using the formula:
θ = s ÷ r
where s is the arc length and r is the radius. Once you know the central angle, you can then use the sector area formula above.
If you prefer everything in one equation, you can combine the two equations and find the sector area with the following formula:
sector area = r × s / 2
How do you find the arc length of a sector?
To find the arc length of a sector s, you can use the formula:
s = r × θ
where r is the radius and θ is the central angle.
How do you find the central angle of a sector?
To find the central angle of a sector θ, you can use the formula:
θ = s ÷ r
where s is the arc length and r is the radius.