Arc Length Calculator
Find the arc length of a sector by entering the central angle and radius in the calculator below.
Results:
Arc Length (s)
Sector Area (A)
Chord Length (a)
On this page:
- Calculator
- How to Calculate Arc Length
- Arc Length Formula
- Find Arc Length using the Radius and Chord Length
- Find Arc Length using the Central Angle and Chord Length
- Find Arc Length using Sector Area and Central Angle
- How to Find Chord Length
- How to Find Sector Area
- Major Arc vs. Minor Arc
- Frequently Asked Questions
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
Ethan has a PhD in astrophysics and is currently a satellite imaging scientist. He specializes in math, science, and astrophysics.
How to Calculate Arc Length
Arc length is a measurement of distance along the circumference of a circle or sector between two points. Put another way, an arc is the curved outer edge, or circular portion, of a sector.
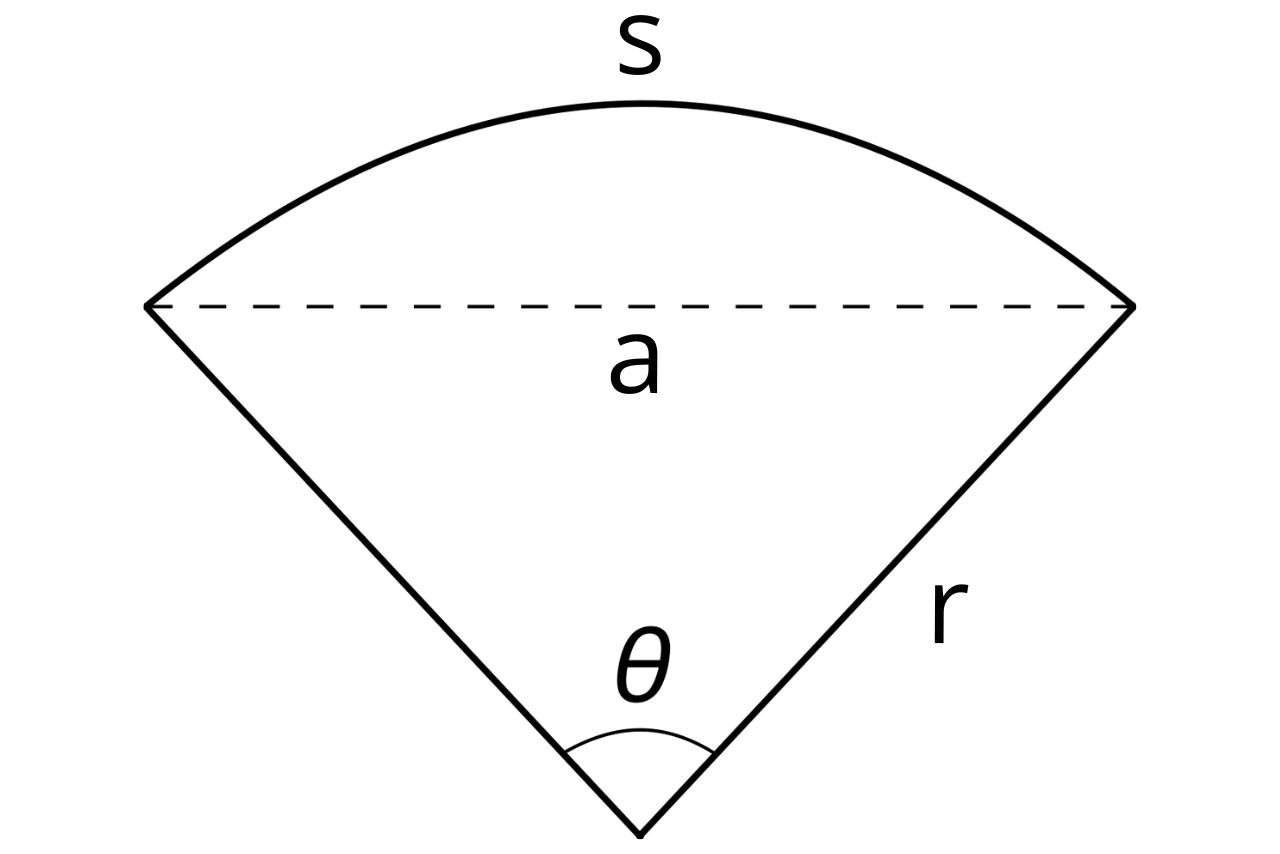
A sector is a portion of a circle shaped like a pie slice, composed of two line segments stretching between the center of the circle and the circle’s edge, and an outer curve of the circle called the arc. Because the line segments stretch from the center of the circle to its edge, they, by definition, are the radii of the circle.
A sector has a central angle, which is the angle between the radii, and a chord, which is the angle spanning the gap between the radii. The sector also has a chord, which is the linear distance between the radii where they meet the arc.
Semicircles, quadrants, and slices of pizza or pie are just some examples of sectors.
You can find the length of the sector’s arc using an easy formula.
Arc Length Formula
For a given radius r and central angle θ, the following formula defines the arc length s of a sector.
s = r × θ
Thus, the length of an arc is equal to the radius r of the sector times the central angle in radians. Note that the central angle must be in radians, not degrees, because the units must be the same on both sides of the equation.
Arc length has units of distance, as does radius, so if the central angle were in degrees, we would have distance = degree-distance which does not make sense. Radians are considered unitless, so by using radians for the angle, the units will be correct.
If you have an angle measured in degrees, you can convert it to radians by multiplying the angle by π divided by 180. You can also use our degrees to radians converter to convert degrees to radians.
In addition, if you don’t know the radius of the circle, but you do know its diameter, then you can find the radius by dividing the diameter by two.
For example, let’s find the arc length of a sector with a radius of 7 meters and a central angle of 2 radians.
arc length (s) = 7 m × 2 rad
arc length (s) = 14 m
Thus, the arc length s is equal to 14 meters.
Find Arc Length using the Radius and Chord Length
If you know the radius and chord length, but you don’t know the central angle, then you need to find the central angle first in order to use the formula above.
Given this information, you can find the central angle of a sector with the formula:
θ = 2 × sin-1(a / 2r)
The central angle θ in radians is equal to 2 times the inverse sine function of the chord length a divided by 2 times the sector radius r. If using units, the chord length and the radius must have the same units.
Now, you can use the central angle and radius to find the arc length using the formula above.
Find Arc Length using the Central Angle and Chord Length
If you know the central angle and chord length, but you don’t know the radius, then you need to find the radius before you can use the arc length formula.
By solving the above formula for the radius, you can find the radius of a sector with the formula:
r = a / 2 × sin(θ ÷ 2)
The radius r of a sector is equal to the chord length a divided by the quantity 2 times the sine of the central angle θ divided by 2.
Using the radius and the central angle, you can use the formula above to find the length of the arc.
Find Arc Length using Sector Area and Central Angle
You can also find the length of the arc if the sector area and central angle are known using the formula:
arc length (s) = 2θ × A
The arc length s is equal to the square root of 2 times the central angle θ in radians, times the sector’s area A divided by θ.
How to Find Chord Length
A sector is divided by the chord into a triangle and an outer segment. The chord, represented as line a in the sector image above, is the line that connects the points where the radii intersect the arc.
The chord length will always be shorter than the arc length, since the chord is the straight-line distance between the two points, while the arc is the curved distance between them.
The length of the chord can be found using the following formula:
chord (a) = 2r × sin(θ / 2)
Thus, the length of the chord a is equal to 2 times the radius r times the sine of the central angle θ divided by 2.
How to Find Sector Area
The area of a sector can be found using the formula:
sector area (A) = r² × θ / 2
The area of a sector A is equal to the radius r squared times the central angle θ, divided by 2.
Try our area calculator to calculate the area of a sector and several other shapes.
Major Arc vs. Minor Arc
When two points on a circle divide the circumference into two arcs, the major arc is the larger arc, and the minor arc is the smaller arc.
The major arc is the arc that connects the two points with a central angle greater than 180°, while the minor arc is the arc that connects the two points with a central angle less than 180°.
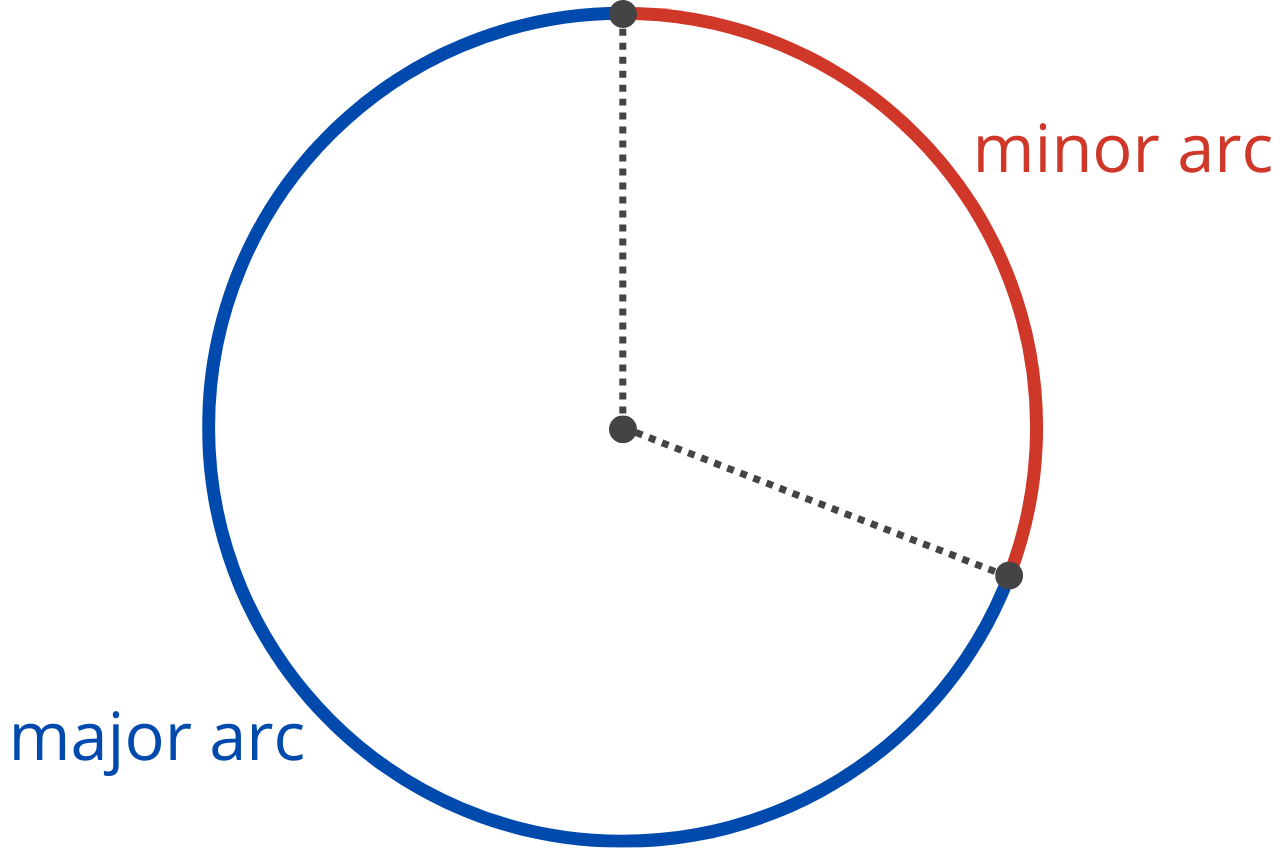
When the two arcs connecting the points measure exactly 180°, the circle is divided into two semicircles. In this case, the arc length is equal to half the circumference of the circle.
Frequently Asked Questions
How do you find the arc length using a central angle in degrees?
To find the arc length using a central angle in degrees, first convert the angle to radians by multiplying by π and dividing by 180. Then use the radius, r, and the central angle, θ (now in radians), to calculate the arc length, s, using the formula:
s = r × θ
How do you calculate an arc length without the radius?
To calculate the arc length without knowing the radius, you must know the central angle and either the area of the sector, the length of the chord, or the area of the entire circle from which the sector is a part of.
If you know one of the former two, check the above sections for the appropriate formula to use. If you know the area of the entire circle, C, then the area of the sector, A, can be found using the following formula:
A = C × 2 × π ÷ θ
You can then calculate the arc length using this area.
Is arc length the same as the angle?
No, the angle describes the span between two radii of a circle, while the arc length is the distance along the curve between those two radii.
What is the arc length of 90 degrees?
The arc length of a central angle of 90 degrees is equal to one-quarter of the entire circumference of the circle.