Circumference Calculator
Calculate the circumference of a circle using the radius, diameter, or area with the calculator below.
On this page:
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
Ethan has a PhD in astrophysics and is currently a satellite imaging scientist. He specializes in math, science, and astrophysics.
How to Find the Circumference of a Circle
A circle is a round, two-dimensional shape with no corners or straight edges where each point along its edge is equidistant from its center point. The circumference is the distance around the outside of a circle, also known as the perimeter of a circle.
If the path around the circle were flattened out into a straight line, the circumference would equal the length of the line. A circle is also defined by its radius, which is the length of a line from the center point of a circle to the outer edge.
Another defining feature is its diameter, which is the length of a line from an edge of a circle to the opposite edge passing through the center of the circle. The diameter is equal to twice the length of the radius.
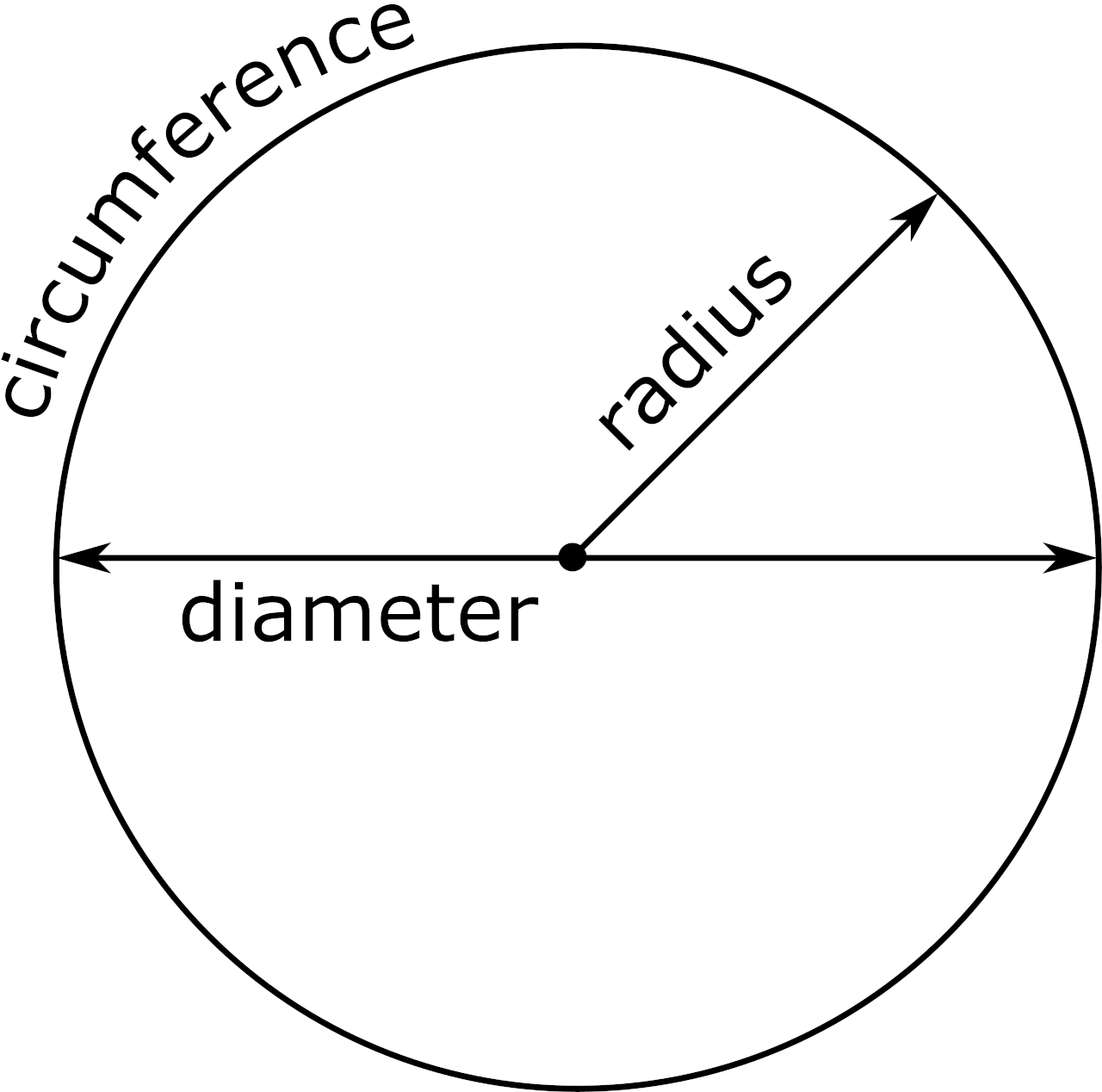
Circumference Formula
You can find a circle’s circumference using its radius and the constant π using the formula:
C = 2πr
The circumference C is equal to 2 times pi times the radius r of the circle r.
Pi is a mathematical constant with an approximate value of 3.141592… Pi can also be approximated as the fraction 22/7, but because it’s an irrational number, it cannot be expressed precisely as a fraction.
Diameter to Circumference Formula
Since the diameter is twice the length of the radius, the formula to find the circumference given the diameter is:
C = πd
The circumference C is equal to pi times the diameter of the circle d.
Area to Circumference Formula
The area is the amount of space the circle occupies. The formula to calculate the circumference given the area of a circle is:
C = 2 × π × A
The circumference C is equal to 2 times the square root of pi times the area A of the circle.
How to Find the Diameter From Circumference
It is possible to solve for the diameter of a circle using its circumference. Since we already know how to find the circumference from the diameter, simply solve the above equation for diameter:
d = C / π
Thus, the diameter d of a circle is equal to the circumference C divided by pi.
This is the same formula that our circumference to diameter calculator uses to solve this problem.
Frequently Asked Questions
Why is the circumference 2πr?
The formula to find circumference is defined as πd since π is a ratio of a circle’s circumference to its diameter. The diameter of a circle is equal to twice the length of the radius, so the formula 2πr is equivalent to πd for determining the circumference.
Is circumference 2πr or πd?
The formulas 2πr and πd are equivalent ways to find the circumference of a circle. Since a circle is most frequently defined in terms of its radius, the formula 2πr is the most commonly used circumference formula.
Is the radius half the circumference?
Not quite. The radius of a circle is equal to half of its diameter, but it is not equal to half the circumference. The diameter is equal to the circumference divided by π, so the radius is equal to the circumference divided by π divided by 2.
This can be simplified to the following formula:
r = C ÷ 2π
The radius r is equal to the circumference C divided by 2 times pi.
Are circumference and perimeter the same thing?
Yes! The circumference is essentially the perimeter of a circle. The circumference is more specifically defined as the boundary of a curved geometric figure, so when working with circles, the term circumference is used to express its perimeter.
Is there a formula for the circumference of an ellipse?
Unfortunately, the circumference of an ellipse cannot be precisely defined, but there are several formulas that can calculate it with good approximation.
One formula to approximate the circumference of an ellipse is:
C = π( 3(a + b) – √[(3a + b)(a + 3b)] )
The circumference C of an ellipse is approximately equal to pi times 3 times the semi-major axis a plus the semi-minor axis b, minus the square root of 3 times a plus b, times a plus 3 times b.
How do you find the circumference of a sphere?
The circumference of a sphere is equal to the distance around a plane that passes through its center point, called a great circle. Since the two-dimensional slice of the sphere is a circle, the formula to find the circumference of a sphere is the same as the formula for a circle.
C = 2πr
The circumference of a sphere is equal to 2 times π times the sphere’s radius r.
If you want to calculate the surface area of the sphere, use the formula:
SA = 4πr
Where SA is the surface area and r is the radius of the sphere.