Circle Calculator
Solve the radius, diameter, area, and circumference of a circle using the calculator below.
On this page:
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
Ethan has a PhD in astrophysics and is currently a satellite imaging scientist. He specializes in math, science, and astrophysics.
Properties of a Circle
A circle is a round, symmetrical shape with no corners or sharp edges where each point along its edge is equidistant from the center. A circle has many properties, such as the radius, diameter, circumference, and area.
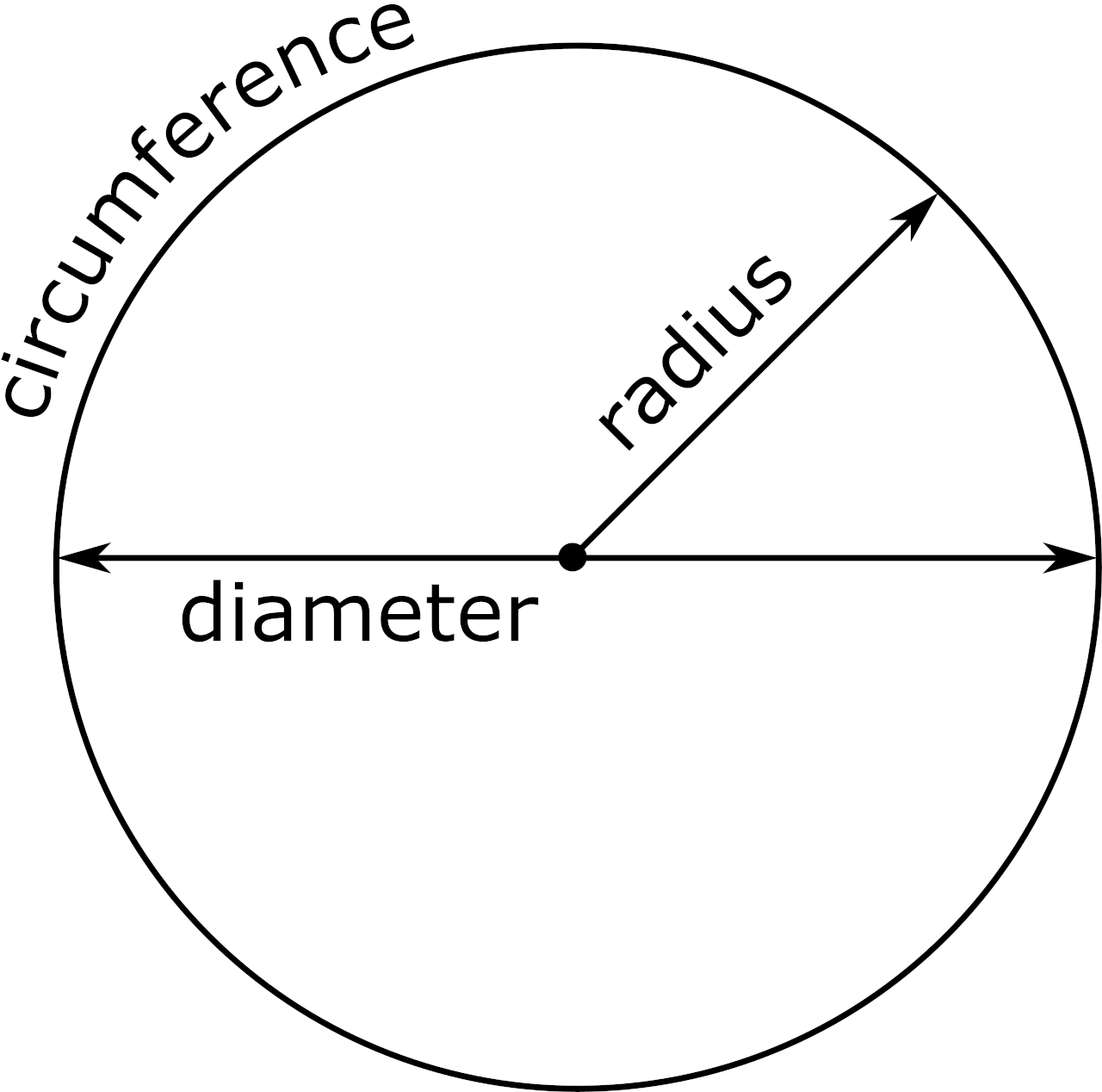
The radius is the length of a straight line from the center to any point on the outer edge.
The diameter is the length of a straight line from one edge to the opposite edge that passes through the circle’s center. It is equal to twice the length of the radius.
The circumference is the distance around the outside edge, also known as its perimeter.
The area is the amount of space a circle occupies in a two-dimensional plane.
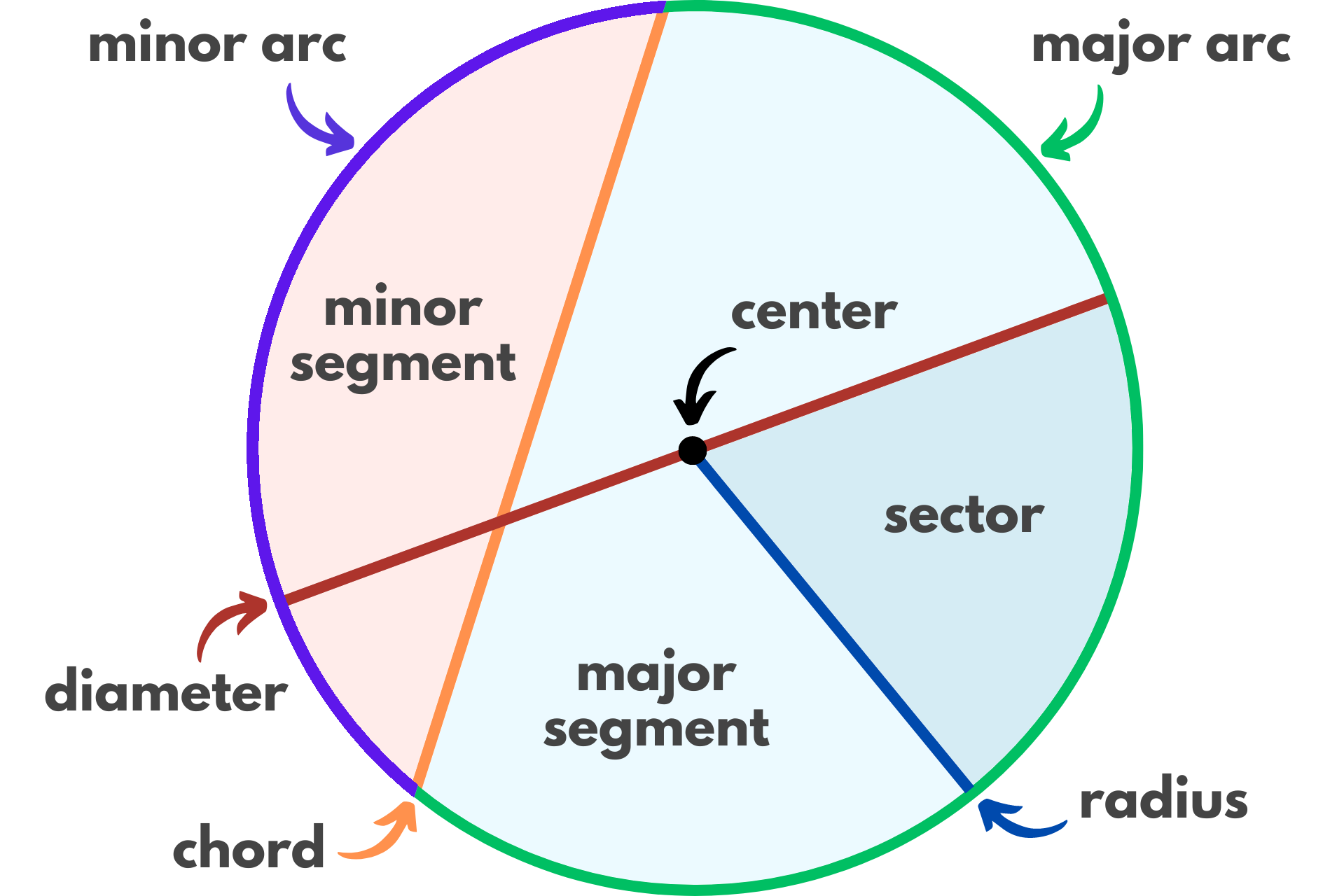
An arc is some fraction of the circle’s outer edge, spanning some central angle. A central angle is an angle that defines a pie-shaped slice of a circle. If a circle is divided into two arcs, the larger arc is known as the major arc, and the smaller arc is known as the minor arc.
A chord is a line that connects two points on the circle’s edge that does not have to pass through the center. If it does pass through the center, the chord is equal to the diameter of the circle.
A segment is any section of a circle that is bounded by both a chord and an arc.
The center point of the circle is the point the circle is centered around. All points on the circle’s edge are equidistant from the center point, a distance equal to the circle’s radius.
A sector is the area bounded by any two radii and the circle’s edge.
How to Find the Radius of a Circle
You can find the radius of a circle using one of the following formulas.
Given the Diameter
The radius of a circle is equal to half the circle’s diameter. The following formula defines the radius given the diameter:
r = d / 2
The radius r is equal to the diameter d divided by 2.
Given the Area
If you know the area of a circle, then you can rearrange the area formula to find the radius.
r = A ÷ π
The radius r is equal to the square root of the area A divided by pi.
Given the Circumference
If the circumference is known, then you can find the circle’s radius using the formula:
r = C / 2π
The radius r is equal to the circumference C divided by 2 times pi.
You can use this same formula to find the diameter as well, learn more on our circumference to diameter calculator.
How to Calculate the Area of a Circle
You can find the area of a circle using a calculator, or you can use the circle area formula:
A = πr²
The area A is equal to pi times the radius r squared.
How to Find the Circumference
You can find the circumference of a circle using a calculator, or you can use the circumference formula:
C = 2πr
The circumference C is equal to 2 times pi times the radius r.
You can also solve for many of these properties of an oval using our ellipse calculator.
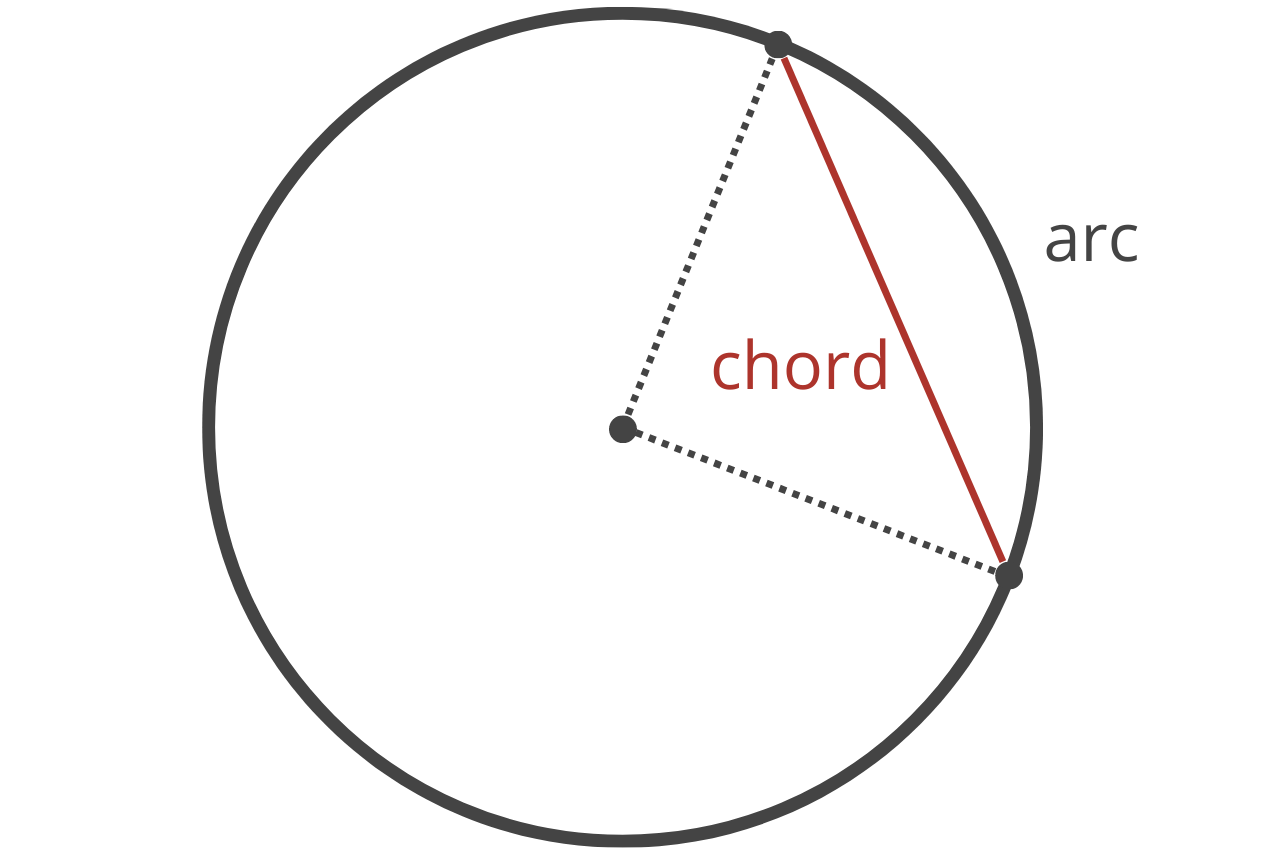
Chords and Sectors
A straight line through a circle that does not pass through the center point is called a chord. A chord connects two points on the edge of the circle. If two lines are also drawn, each connecting the center of the circle to the points where the chord intersects the circle’s edge, then the newly formed bounded area is called a sector.
A sector is a pie-slice portion of a circle bounded by two radii and an arc of the circle’s edge connecting the two radii.
You can find the area of a sector using the formula:
A = r² × θ / 2
The area A is equal to the radius r squared times the central angle θ in radians, divided by 2. Note that the central angle must be in radians to use this formula.
If the central angle is in degrees, you can find the area of the sector using the following formula:
A = πr² × θ / 360
You can also use our degrees to radians converter to convert the angle to radians and use the first formula.
You can find the length of a chord using the following formula:
a = 2r × sin(θ / 2)
The length of chord a is equal to 2 times the radius r times the sine of the central angle θ divided by 2.
You can find the arc length using the following formula:
s = rθ
The length arc s is equal to the radius r times the central angle θ in radians.
Unit Circle
The unit circle is a circle with a radius equal to 1, centered on the origin (0, 0). It is used to calculate the cosine, sine, and tangent of any angle within the circle, although it is most commonly used for easy memorization of the sine and cosine of angles that are multiples of 30 or 45 degrees.
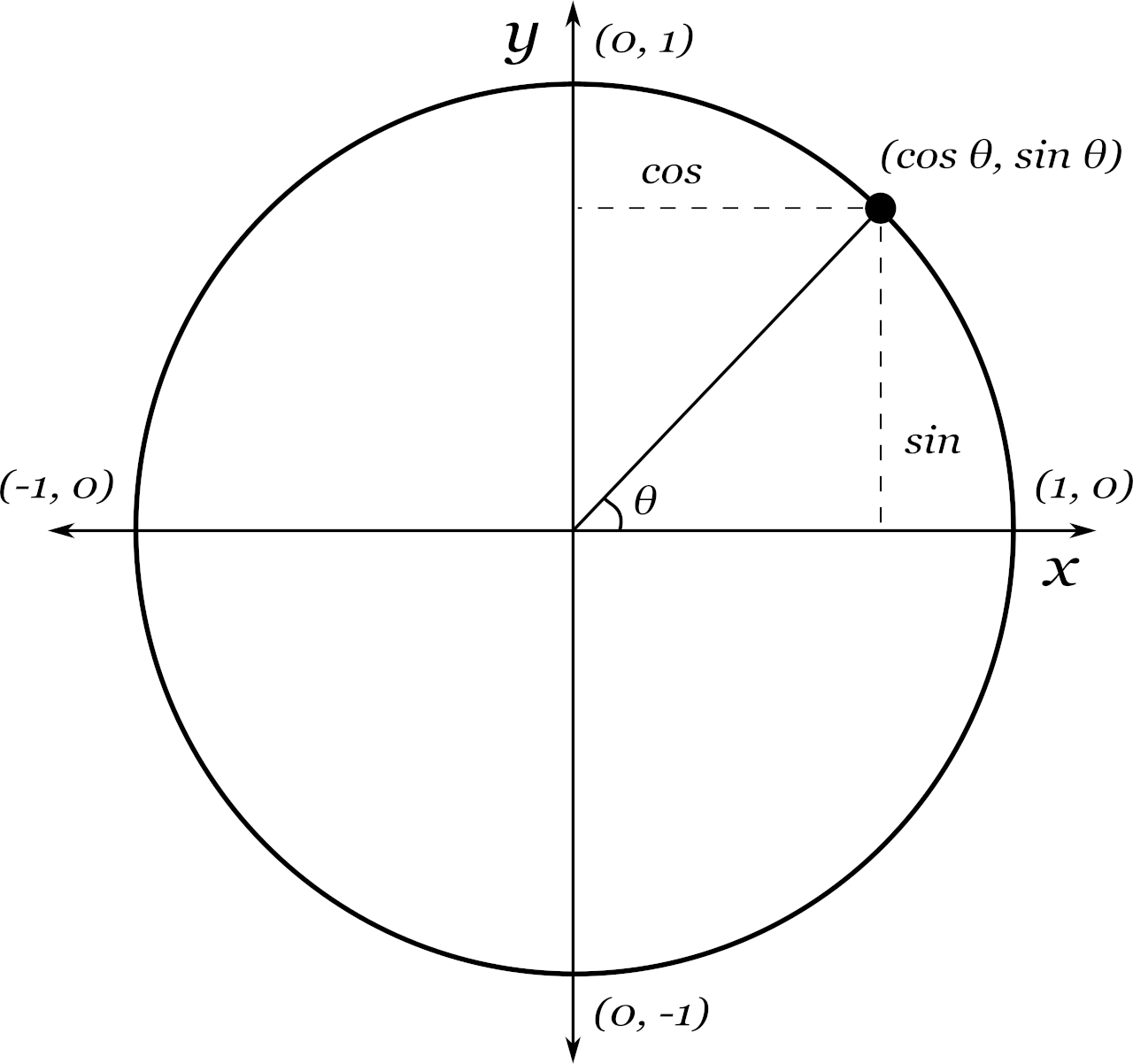
The unit circle defines how to find the sides and angles of a right triangle that is formed when extending a line with a known central angle within the circle.
Because the unit circle has a radius equal to 1, the triangle’s hypotenuse is also always equal to 1.
The side of the triangle opposite the angle θ is equal to the sine of the angle, while the base is equal to the cosine.
Frequently Asked Questions
Why is pi used in a circle?
Pi is actually a naturally occurring number that was discovered by trying to calculate the area of a circle!
If you try to calculate the area of a circle using different polygons that approximate a circle, and then relate that value to the radius of the circle, then you’ll find that you’ll get closer and closer to the value of pi the better your approximation becomes.
How do you find the center of a circle?
One way to find the center of the circle is simply to find the point that all points on the circle’s edge are equidistant from. Another way is to find two points on the circle’s edge that are directly across from each other and connect them with a line.
The center of the circle will then be half the distance between those two points.
What do we use circles for?
Circles are used all the time in math, geometry, physics, and art! For example, you need to know the circumference of the wheels of a vehicle (which are circles) in order to know how far the vehicle will travel with each revolution of the wheels.