Ellipse Calculator
Find the area, circumference, foci distance, eccentricity, vertices, and standard form equation of an ellipse using the calculator below.
Properties of the Ellipse:
| Semi-Major Axis: | |
|---|---|
| Semi-Minor Axis: | |
| Area (A): | |
| Circumference (C): | |
| Eccentricity (e): | |
| Foci Distance (c): |
Standard Form Equation:
Graph Coordinates
| First Focus: | |
|---|---|
| Second Focus: | |
| First Vertex: | |
| Second Vertex: | |
| First Co-Vertex: | |
| Second Co-Vertex: |
On this page:
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
Ethan has a PhD in astrophysics and is currently a satellite imaging scientist. He specializes in math, science, and astrophysics.
What is an Ellipse?
An ellipse is a two-dimensional rounded shape that looks like a regular oval, whose curve consists of points in which the sum of the distances from both foci are the same for any point in the curve.
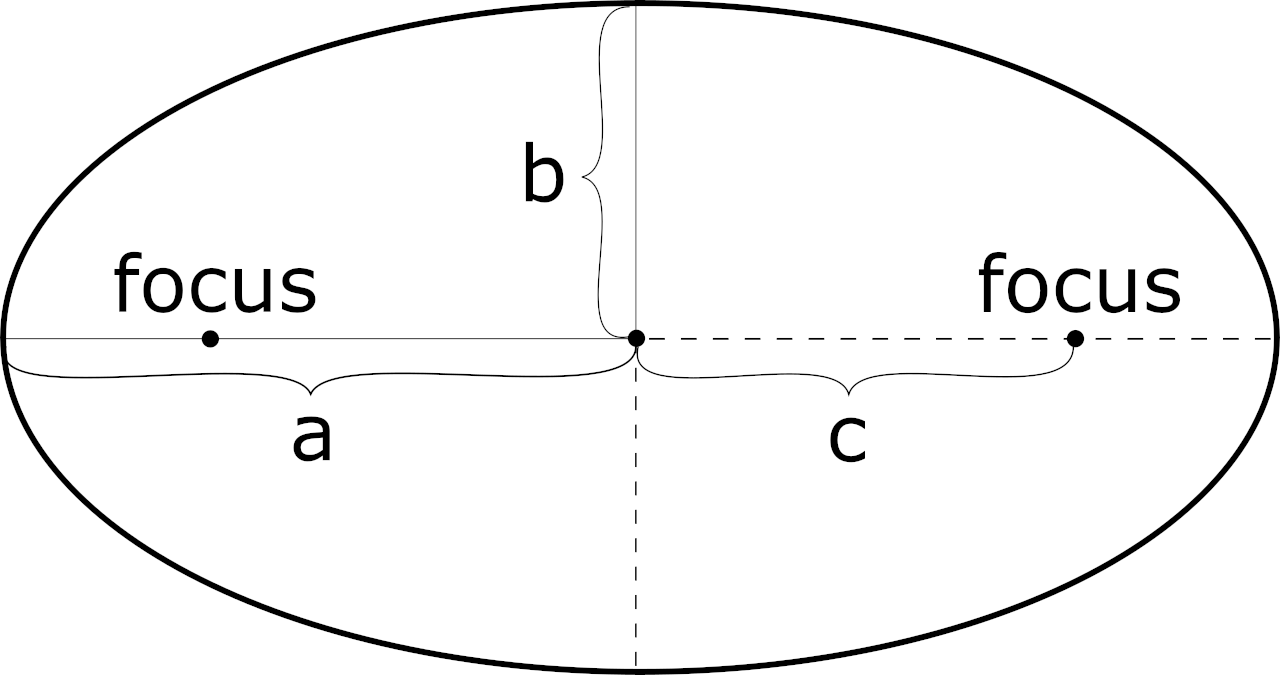
The foci (plural of focus) are the two points within the ellipse that define its outer curve based on the aforementioned criteria. The foci are different points than the center of the ellipse, except in the case of a circle, in which case they are the same.
While an ellipse is oval in shape, it differs from an oval in that it is mathematically defined, while any curve resembling a squashed circle is an oval.
An ellipse is described by the distance from its center to the maximum horizontal and vertical extent of the curve. These maximum extents lie on the semi-major and semi-minor axes that bisect the ellipse horizontally and vertically.
The semi-major axis is defined as the distance between the center of the ellipse and the maximum horizontal or vertical extent of its curve (also known as its horizontal or vertical vertex), whichever is greater. The semi-minor axis is defined as the lesser of the maximum horizontal and vertical extents of the ellipse’s curve.
Ellipse Equation
Using the semi-major axis a and semi-minor axis b, the standard form equation for an ellipse centered at origin (0, 0) is:
x2 / a2 + y2 / b2 = 1
Where:
a = distance from the center to the ellipse’s horizontal vertex
b = distance from the center to the ellipse’s vertical vertex
(x, y) = any point on the circumference
When an ellipse is oriented horizontally, then the value of a is greater than b, and when it is oriented vertically, then the value of a is less than b.
For an ellipse that is centered at a point other than the origin (0, 0), the standard form equation for the ellipse is:
(x – h)2 / a2 + (y – k)2 / b2 = 1
Where:
a = distance from the center to the ellipse’s horizontal vertex
b = distance from the center to the ellipse’s vertical vertex
(h, k) = center of the ellipse
(x, y) = any point on the circumference
Note: the definitions of a and b above assume the semi-major axis aligns with the horizontal axis. If it instead aligns with the vertical axis, then a is the distance from the center to the ellipse’s vertical vertex, and b is the distance from the center to the ellipse’s horizontal vertex.
Put more simply, and without having to change definitions, when an ellipse is oriented horizontally, then the value of a is greater than b, and when it is oriented vertically, then the value of a is less than b. But whichever value is greater is referred to as the semi-major axis, and whichever is smaller is referred to as the semi-minor axis.
How to Find the Area of an Ellipse
Area is the space occupied by a two-dimensional geometric shape. The area of an ellipse can be found using a simple formula.
A = πab
Thus, the area A is equal to pi times the semi-major axis a times the semi-minor axis b.
This is very similar to the formula to find the area of a circle, but instead of multiplying a single radius by itself, the product of both axes is used.
How to Find the Circumference of an Ellipse
The circumference is the distance around a two-dimensional geometric shape, sometimes referred to as the perimeter.
Interestingly, the circumference of an ellipse cannot be exactly defined by simple mathematics, but several formulas can approximate it with varying degrees of accuracy.
A relatively simple and fairly precise formula to find the circumference of an ellipse is:
C ≈ π( 3(a + b) – (3a + b)(a + 3b) )
The circumference C is approximately equal to pi times 3 times the semi-major axis a plus the semi-minor axis b, minus the square root of 3 times a plus b, times a plus 3 times b.
When the semi-major axis is equal to the semi-minor axis, the circumference formula reduces to the circumference of a circle. Let’s see this for ourselves:
First let a = b = r:
C = π( 3(r + r) – (3r + r)(r + 3r) )
C = π( 3(2r) – (4r)(4r) )
C = π( 6r – 16r² )
C = π( 6r – 4r )
C = 2πr
Pretty cool! Try our circumference calculator to find the circumference of a circle.
How to Find the Foci Distance
An ellipse has two focus points, pluralized foci. The distance from the center point of the ellipse to each focus is called the foci distance.
The formula to find the foci distance for an ellipse is:
c = a² – b²
The foci distance c is equal to the square root of the semi-major axis a squared minus the semi-minor axis b squared.
How to Find the Eccentricity of an Ellipse
The eccentricity of an ellipse is the ratio of the foci distance to the semi-major axis length. Eccentricity can be thought of as how elongated the ellipse looks.
The smaller the eccentricity, the closer the ellipse is to becoming a circle.
When the eccentricity equals zero, the ellipse is a circle. When it equals one, the ellipse actually becomes a parabola, and when it is greater than one, the ellipse becomes a hyperbola.
The formula to find the eccentricity of an ellipse is:
e = c / a
The eccentricity e is equal to the foci distance c divided by the semi-major axis length a.
How to Graph an Ellipse
You can graph an ellipse by plotting its major properties on the graph, then drawing a line where the sum of the distances to the foci are all equal. For an ellipse centered at the point (h, k), you can plot the foci and vertices at the following points:
- first focus: (h – c, k)
- second focus: (h + c, k)
- first vertex: (h – a, k)
- second vertex: (h + a, k)
- first co-vertex: (h, k + b)
- second co-vertex: (h, k – b)
For a horizontal ellipse (a > b), you can plot any point on the circumference of the ellipse using the standard form equation above.
(x – h)2 / a2 + (y – k)2 / b2 = 1
For a vertical ellipse (a < b), swap a and b in the standard form equation.
(x – h)2 / b2 + (y – k)2 / a2 = 1
To plot the line, substitute any x value less than a to find the corresponding y coordinate and any y value less than b to find the corresponding x coordinate.
Another way to plot the ellipse that might be more familiar is to solve the standard equation above for y:
y = k ± b × 1 – ((x – h) ÷ a)²
Now you can enter a value for x and find its corresponding y-value to plot. Keep in mind, though, that the radical (the value inside the square root) must be greater than or equal to zero.
You might also be interested in trying our circle calculator.
Frequently Asked Questions
Is an ellipse a circle?
Not quite. While an ellipse is not a circle, a circle is actually a special type of ellipse. A circle is an ellipse where the semi-major axis and semi-minor axis are equal in length.
What are the two types of ellipse?
The two types of ellipse are the horizontal major axis ellipse and the vertical major axis ellipse. The difference between the two is that the former has the semi-major axis parallel to the horizontal, or x-axis, while the latter has the semi-major axis parallel to the vertical, or y-axis.
What is the use of an ellipse in real life?
Ellipses are super important in real life! In fact, the orbit of every planet around a star, including the orbit of all planets in our solar system around the sun, is an ellipse. So we need to use ellipses in order to explore the solar system!