Segment Area Calculator
Calculate the area and height of a segment by entering the central angle and radius in the calculator below.
Results:
Segment Area (A)
Segment Height (h)
Arc Length (s)
Chord Length (a)
On this page:
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
Ethan has a PhD in astrophysics and is currently a satellite imaging scientist. He specializes in math, science, and astrophysics.
How to Calculate the Area of a Segment
A segment is a part of a circle separated by a chord connecting two points on the circle’s edge. Think of a segment as a part of a circle that has been sliced off using a straight line.
A segment is often represented as part of a sector, as seen in the image below. The segment is the shaded part of the sector.
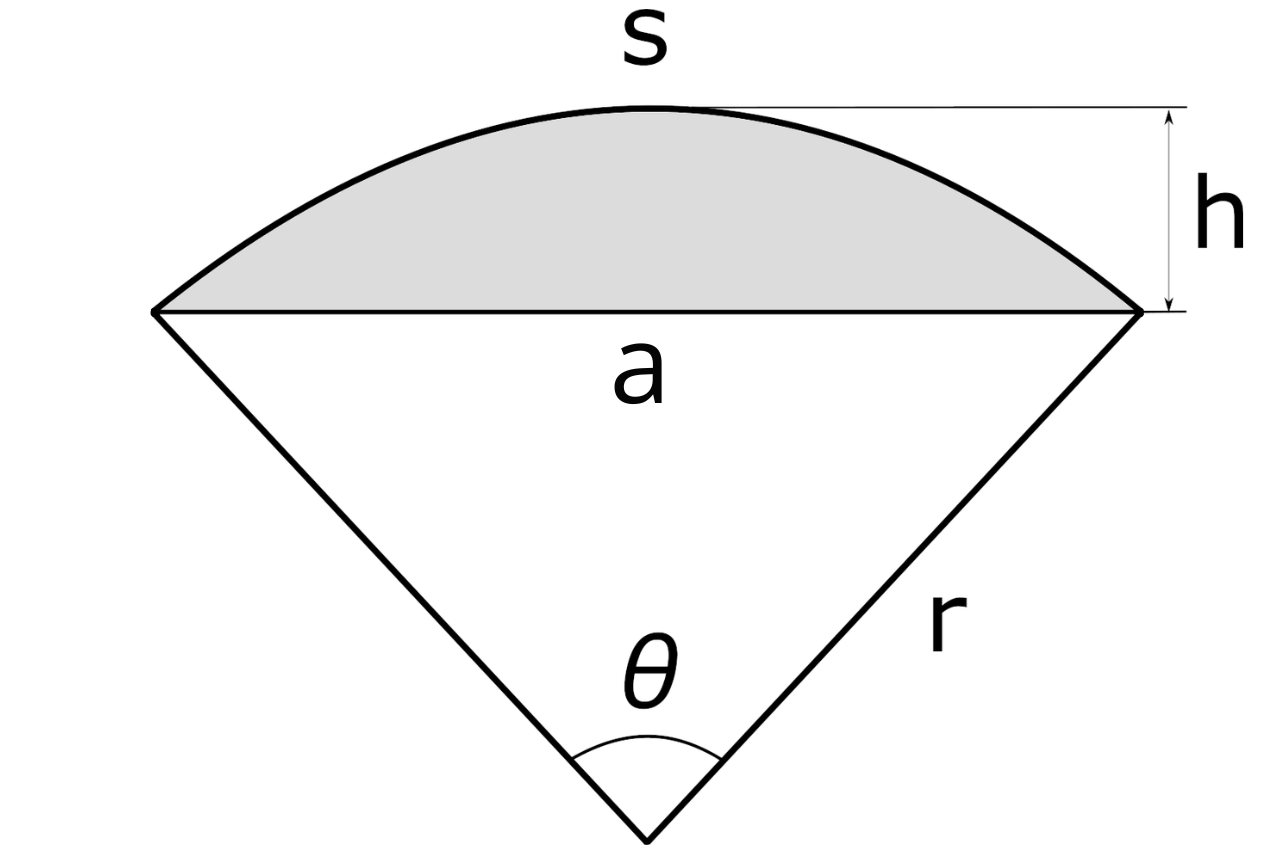
In addition to area, a segment is defined by its height (also called the sagitta), chord length, and arc length. The area of a segment can be found using a simple formula.
Segment Area Formula
The area can be found using the segment area formula:
segment area = r² × (θ – sin(θ)) / 2
Thus, a segment’s area is equal to the radius r squared, times the central angle θ in radians minus the sine of θ, divided by 2.
Note that the central angle must be in radians for this equation to work. If you have the central angle in degrees, use our degrees to radians converter to convert to radians, or use the equation in the next section.
For example, let’s find the area of a segment for a circle with a radius of 17 and a central angle of 1.25 radians.
segment area = 17² × (1.25 – sin(1.25)) / 2
segment area = 289 × (1.25 – 0.094898) / 2
segment area = 289 × 0.301021) / 2
segment area = 86.995 / 2
segment area = 43.497
Thus, the segment area is 43.497.
Segment Area Formula for a Central Angle in Degrees
If you want to find the area of a segment, but your central angle is in degrees instead of radians, you can find the area using the following formula:
segment area = r² × ((θ × π)/360 – sin(θ))/2
This is essentially the same formula as above, but the (θ × π)/360 part converts the angle to radians.
How to Find the Height of a Segment
The following formula defines the height, or sagitta, of a segment.
segment height = r × (1 – cos(θ / 2))
The height of a segment is equal to the radius r times 1 minus the cosine of the central angle θ in radians divided by 2. Note here that again, the central angle must be in radians, not degrees.
How to Find the Arc Length of a Segment
The arc of a segment is the rounded outer portion of the circle that connects the two radii of the circle. The arc length can be found using the formula:
arc length (s) = radius (r) × central angle (θ)
The arc length s of a segment is equal to the radius r times the central angle θ in radians. Again, as with most of the above equations, the central angle must be in radians, not degrees.
You might also be interested in our sector area calculator for solving the parts of a sector.