Central Limit Theorem Calculator

Enter the population mean, population standard deviation, and sample size to calculate the sample mean and standard deviation using the central limit theorem (CLT).

Population Mean (μ):

Population Standard Deviation (σ):

Sample Size (n):

×

Have a Question or Feedback?

Name (optional)

Email (optional)

Question or Feedback

Contact Us

Results:

Sample Mean (μ_x̄)

 

Sample Standard Deviation (σ_x̄)

 

---

Steps to Solve Using the Central Limit Theorem

Find the Sample Mean

Provided the sample is sufficiently large, the sample mean will be equal to the population mean

μ_x̄ = μ

Find the Sample Standard Deviation

The central limit theorem provides the following formula to solve the standard deviation for a sample

σ_x̄ = σ / √n

Learn how we calculated this below

scroll down

Add this calculator to your site

---

On this page:

• Calculator
• How to Use the Central Limit Theorem
• Central Limit Theorem Formula
• Sample Mean Formula
• Sample Standard Deviation Formula
• How to Find Probabilities Using the Central Limit Theorem
• References

---

By

Joe Sexton

Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.

Full bio

Reviewed by

Brian Libgober, PhD

Brian specializes in political science and statistics with several advanced degrees from Harvard.

Full bio

and

Bailey Nelson, MS

Bailey is an experienced educator and specializes in K-12 math and science. She holds a Master's degree in professional education and holds several teaching certifications.

Full bio

Copy Link Share on Facebook Share on X Share on Pinterest Cite

×

Cite As:

Sexton, J. (n.d.). Central Limit Theorem Calculator. Inch Calculator. Retrieved December 8, 2024, from https://www.inchcalculator.com/central-limit-theorem-calculator/

How to Use the Central Limit Theorem

The central limit theorem for sample means states that as you take larger samples of independent random variables and calculate their means, the sample means form their own normal distribution, which is known as the sampling distribution of the mean. This distribution has the same mean as the original distribution and a variance equaling the original variance divided by the sample size.

Given a known population mean value and a sufficiently large sample, the central limit theorem dictates that the sample mean will equal the population mean. The sample size that is big enough to provide these guarantees depends on context, however in practice rules of thumb about what is good enough can be surprisingly small, for example with some sources proposing samples of 100, 60, 30, or even in some cases as few as 12.^[1]

Again, what approximation is good enough depends on context, but the notion that a sample of 30 or 60 could be sufficient is often surprising to those who have been taught to distrust surveys with fewer than 1,000 respondents.

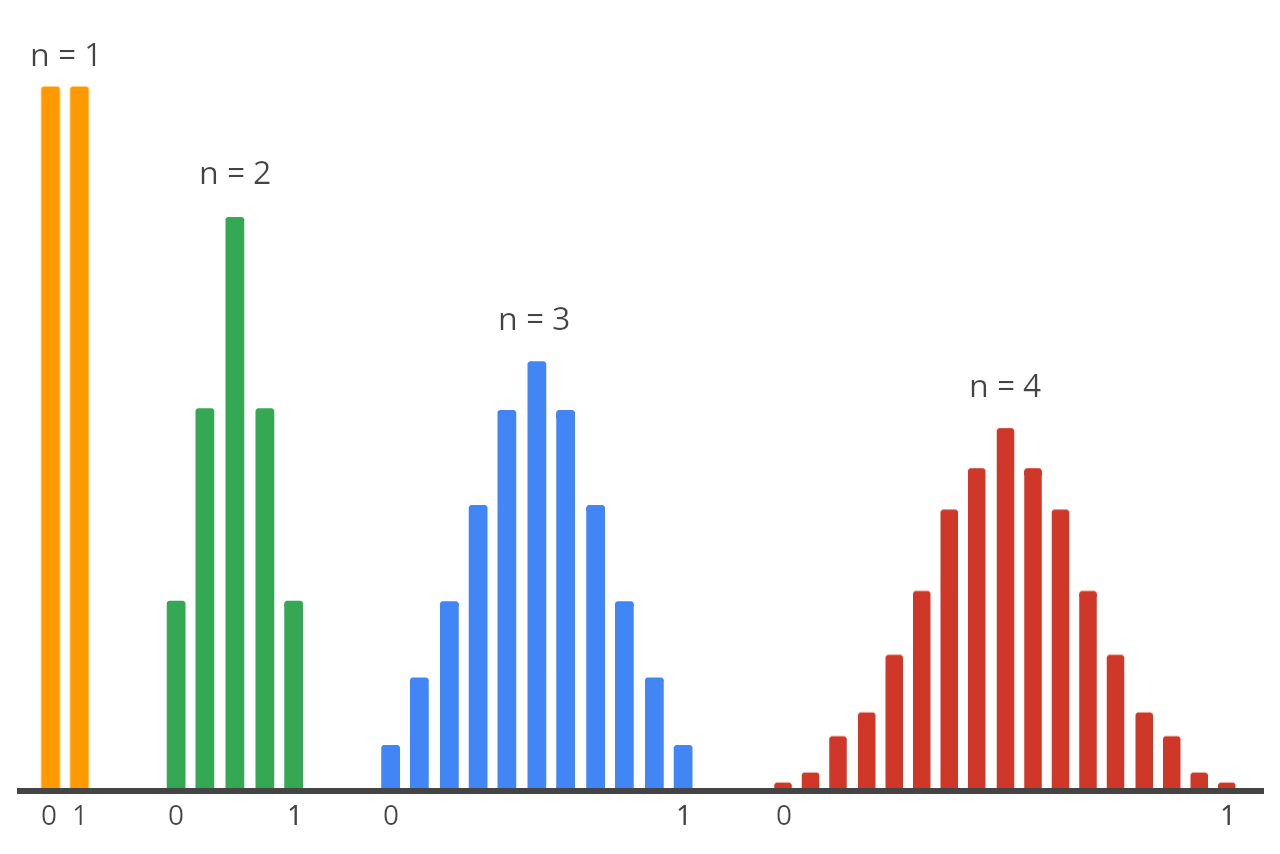
As you can see in the image above, as the sample size n increases, the values of each sample continue to be distributed around an equal mean.

Central Limit Theorem Formula

Using the central limit theorem, you can calculate the mean, standard deviation, and z-score given a sufficiently large sample size with the following formulas.

Remember:
mean: The average of the data set.
standard deviation: The measure of how spread out the values of a dataset are from the mean.
z-score: The measure that quantifies how many standard deviations a specific data point is away from the mean of a distribution.

Let’s dig into each of these in a little more detail.

Sample Mean Formula

You can use the central limit theorem to find the sample mean. If μ is the mean of the population values x, then μ_x̄ is the mean of the sample values x̄.

The sample mean μ_x̄ is equal to the population mean μ.

μ_x̄ = μ

You can use our mean calculator to find the population mean μ.

Sample Standard Deviation Formula

You can also use the central limit theorem to find the standard deviation of a sample σ_x̄, given a known standard deviation of the population σ.

The central limit theorem provides the following formula to calculate the standard deviation of a sample.^[2]

σ_x̄ = σ / √n

Thus, the central limit theorem states that the standard deviation of a sample σ_x̄ is equal to the standard deviation of the population σ divided by the square root of the sample size n.

This is also referred to as the standard error of the mean.

You can use our standard deviation calculator to find the population standard deviation σ.

How to Find Probabilities Using the Central Limit Theorem

The central limit theorem can also be used to find the probabilities of sample means. Start by using the following formula to find the z-score.

z = x̄ – μ_x / σ_x̄

The z-score z is equal to the sample mean x̄ minus μ, which is the average of x and x̄, divided by the sample standard deviation σ_x̄.

Using the z-score, you can look up the probability of getting this mean using a z table or through the normal cumulative distribution function.

By applying a margin of error and confidence interval, we can make estimates on an independent random variable given a data set with a sufficiently large sample size and assess how good those estimates are.