Average Calculator
Find the average value by entering the numbers below.
Average:
Steps to Solve
Step One: Count the Numbers
count = ?
Step Two: Find the Sum of the Numbers
sum = ?
Step Three: Use the Average Formula
average = sum / count
On this page:
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
How to Find the Average
The average, or mean, is a measure of the central tendency of a set of numerical data. It is a single number used to represent a center, or typical value, for a larger set of numbers.
The average is one of the fundamental measurements for a data set in statistics and is used as the basis for several other measurements.
There are several types of averages that include arithmetic averages, geometric averages, weighted averages, and even harmonic averages. The calculator above solves the arithmetic average, also called the arithmetic mean.
You can find the mean using a formula.
Average Formula
The average formula to find the arithmetic mean for a set of numbers is:
average = sum / count
The average of a set of numbers is equal to the sum of the numbers divided by the count of the numbers.
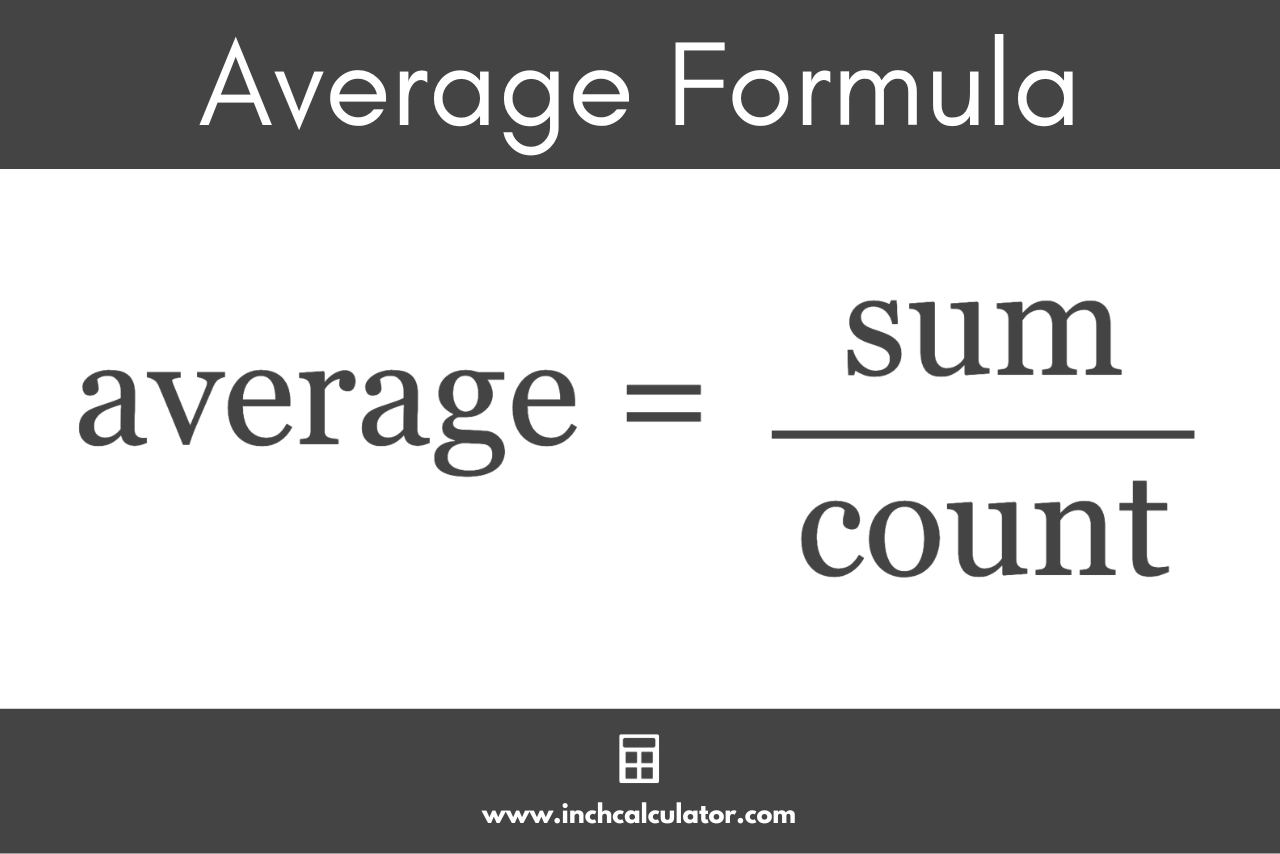
Find the Average in Three Easy Steps
So, you can find the average using the formula above in three steps.
Step One: Find the Count
The first step to find the average is to count the number of elements in the set of data.
Step Two: Find the Sum
The second step is to add all of these numbers together to calculate the total sum.
Step Three: Find the Average
The final step is to use the average formula above by dividing the sum of the numbers by the count. The resulting value is the average of the data.
While the average, or mean, is commonly used, it is just one measure of the center for a data set. Other commonly used measures of center are the median and mode.
In some special cases, geometric and harmonic means might also be used as measures of centrality, although they come up less frequently in most applications than mean, median, and mode.
You can also use our mean, median, mode calculator to find other measures of centrality or representativeness in a set of data.
Median and mode are measurements that are often important to check because the average measurement can be easily skewed by outliers (extreme values) in the data.
For example, if you are trying to find your average grade for the year when you received seven A grades but got two F grades, your average grade might be a B.
But, the median and mode of your grades is an A since they are less skewed by one or two low grades in the whole set, which are outliers.
You can use this process to calculate the average for other types of data as well. For instance, our average time calculator uses this method to calculate the average time given a set of two or more times.
Frequently Asked Questions
What's an average in math?
The average is the measure of the central tendency, or the middle, of a set of numbers.
Does average always mean the mean?
Average and (arithmetic) mean are often used interchangeably, but sometimes people use the term average to refer to the value which best represents the overall data, but given the possibility of outliers the arithmetic mean may or may not be representative of the overall data. Statisticians often avoid using the term average because of possible ambiguities in its interpretation and instead use the more specific terms like mean, median, or mode.
Which is better, average or median?
Neither the average or median is better than the other, it really depends on the purpose and the data. The mean typically works well to represent a data set, which is why it is the more frequently used measure, but it can be misleading if there are outliers or the data is skewed in some way.
What does it mean if average is higher than median?
If the average is higher than the median, that means the data is right-skewed, meaning the tails of the distribution above the median are longer than below. Average incomes are above median incomes, for example, because it is not possible to make less than 0 in income and some people have incomes in the millions or even hundreds of millions of dollars.