Mode Calculator

Find the mode of a set of numbers using the calculator below.

Have a Question or Feedback?

Results:

Mode:

Frequency Table:

Value:	Frequency

Learn how we calculated this below

scroll down

Add this calculator to your site

How to Find the Mode

In statistics, the mode is the most frequently occurring value in a numerical set of data. The mode is the number that occurs most often or is repeated the most.

The mode is a commonly used summary statistic, and it describes the central tendency of the data.

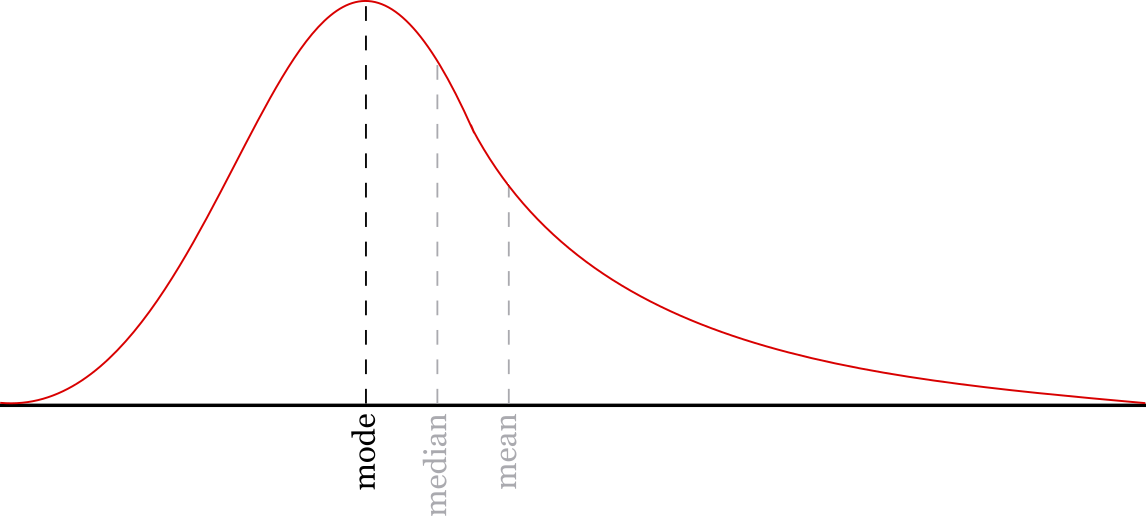
Graph showing the mode compared to the mean and median of the data

The mode of a data set is the most frequently occurring number that arises at least twice. Thus, it is possible for a data set to have no mode at all if there are no numbers that repeat.

For example, given the set [3,5,3], the mode is 3 since it occurs twice.

However, given the set [2,4,7], there is no mode since all of the values only occur once.

It is also possible for a data set to have more than one mode if multiple values occur the same number of times. A set with one mode is referred to as a unimodal dataset, a set with two modes is a bimodal dataset, and a set with three or more modes is a multimodal dataset.

For example, given the set [3,5,3,5,7], the mode is both 3 and 5 since they both occur with the same frequency. This is a bimodal dataset.

Steps to Find the Mode

You can find the mode by counting the number of times each value in a set of numbers is repeated. The number that occurs with the highest frequency is the mode.

While uncommon, it is possible that multiple numbers might be repeated the same number of times. If multiple numbers are repeated the same number of times as the most commonly repeated number, they are also part of the mode.

Some datasets have no mode at all. If no numbers are repeated at all, then there is no mode.

So, to sum it up, there are three simple steps to find the mode:

Step 1: count the occurrences of each number in the set
Step 2: find the number or numbers that occur the most
Step 3: that’s it – you found the mode!

Mode Formula

The process above can be represented using the following mode formula:

\text{mode }= L + \left ( \frac{f_{1}-f_{m}}{2f_{1}-f_{m}-f_{2}} \right ) \times h

Where:
L = lower limit of the modal class
f_m = frequency of the modal class
f₁ = frequency of the class preceding the modal class
f₂ = frequency of the class succeeding the modal class
h = size of the class interval

Graphic showing the mode formula, where the mode is equal to the number(s) with the highest frequency in the set.

Example: Set With a Single Mode

For example, let’s calculate the mode of the following numbers: [3,7,5,7,6,7,3]

Step 1: count the occurrences of each number.

Value:	Frequency
3	2
5	1
6	1
7	3

Step 2: find the number or numbers that occur most often.

Since 7 occurs the most in this set, the mode is 7.

Example: Set With Multiple Modes

For example, let’s calculate the mode of the following numbers: [2,6,5,2,6,4,7,4]

Step 1: count the occurrences of each number.

Value:	Frequency
2	2
4	2
5	1
6	2
7	1

Step 2: find the number or numbers that occur the most.

Since 2, 4, and 6 occur with the same frequency in this set, the dataset is multimodal, and the mode is 2, 4, and 6.

The mode is the least used statistical observation since mean and median are the most commonly used. Try our mean or median calculators.