Probability Calculator
Calculate the probability of two events or a series of events using the calculator below.
Probability Of:
| Intersection of A and B: | |
|---|---|
| P(A∩B): | %
|
| Union of A and B: | |
| P(A∪B): | %
|
| Symmetric Difference of A and B: | |
| P(A∆B): | %
|
| Complement of A and B: | |
| P((A∪B)'): | %
|
| Complement of A: | |
| P(A'): | %
|
| Complement of B: | |
| P(B'): | %
|
| A occurring each time: | %
|
|---|---|
| A never occurring: | %
|
| A occurring at least once: | %
|
| B occurring each time: | %
|
| B never occurring: | %
|
| B occurring at least once: | %
|
On this page:
How to Calculate Probability
Probability is the quantitative expression of the chance of an event occurring. More specifically, if the set of possible events contains n elements, and an event is associated with r elements, and all elements are equally likely, then the probability is the ratio of r/n.
An example of using probability is when rolling dice. For example, you might ask yourself what the chance is that you’ll roll a six? Alternatively, you are asking what the probability is of rolling a six.
To find the probability of something happening, you need to first know the set of possible outcomes. Then, you can apply the probability formula to solve.
Continuing the dice example, there are six possible outcomes when rolling the dice. You can roll a one, two, three, four, five, or six. Each outcome is equally likely. Therefore the chances of rolling a six are 1/6.
Probability Formula
This is the basic formula to solve the probability of a favorable outcome.
P(A) = number of times A can occur / number of possible outcomes
Thus, the probability of result A is equal to the number of possible times A can occur divided by the total number of possible outcomes.
So, continuing the dice example, you might be interested in the probability of rolling an even number. There are three even numbers on the dice, 2, 4, and 6. The probability of rolling an even number is thus 3/6 since there are three even sides on the die and six total sides, each equally likely to turn up.
An example to illustrate the probability of an event where the number of times the event can occur is greater than one would be the odds of drawing a spade from a deck of cards. Since there are 13 cards of each suit and 52 total cards, the probability of drawing a spade is 13/52, which simplifies to 1/4.
It is important that all outcomes be equally likely in order to calculate probabilities in this fashion. For example, if the dice were weighted in some way so that the side opposite the six were much heavier, then the probability of a six arising would likely differ substantially from 1/6. Statistical hypothesis testing can be used to decide if a dice is weighted.
Our combinations and permutations calculators can help find the number of possible outcomes for a data set. This can be used to help solve the probability of an expected outcome.

How to Find the Probability of Independent Events
Things get a little more complicated when more than one possible outcome, or event, can occur. We refer to these as independent events.
For example, you might want to know how to find the probability of getting a six when rolling two dice. In this case, we have two independent events that we need to know the likelihood of.
There are a few different variations of how independent events can occur. Let’s cover each way we could roll a six.
Intersection
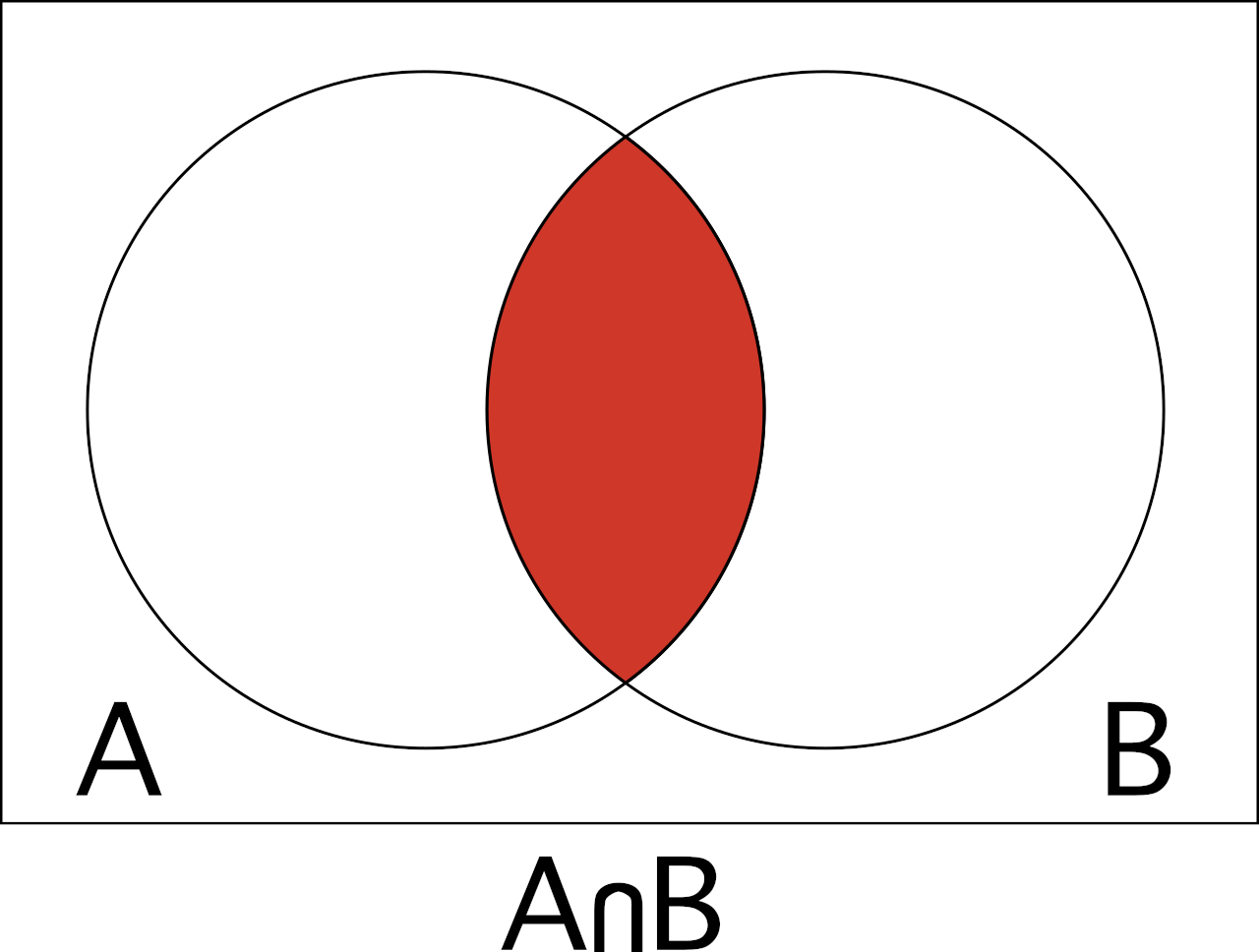
In statistics, the probability of the intersection is the likelihood that both events will occur. In the dice example, this would be the chance of both dice being a six when rolling.
The intersection of events A and B is denoted A∩B, and the Venn diagram above can help visualize the intersection of events.
You can find the probability of intersection of independent events using the following formula:
P(A∩B) = P(A) × P(B)
The probability of intersection P(A∩B) is equal to P(A) times P(B).
Union
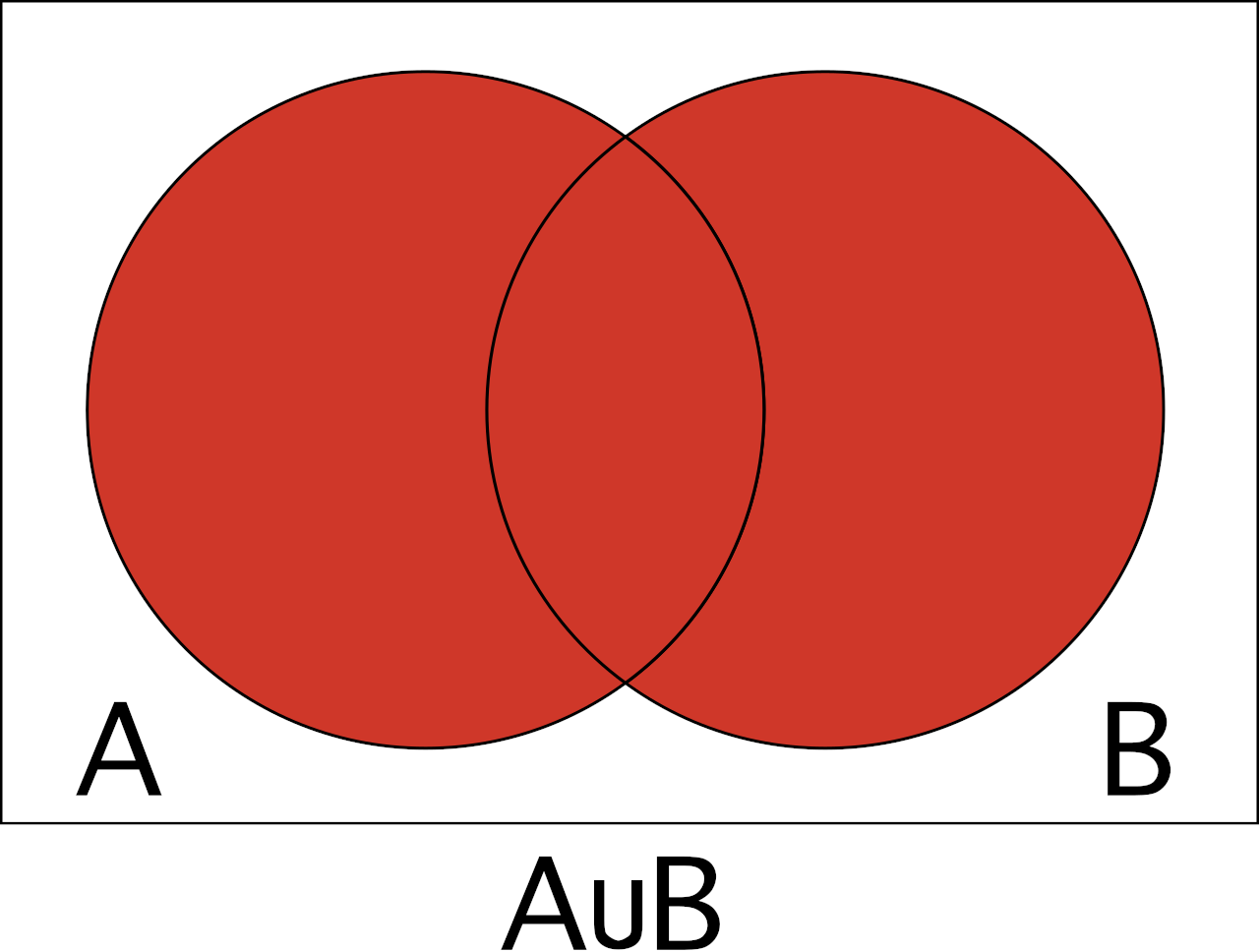
The probability of the union is the likelihood that at least one of the events will occur, or both. In the dice example, this would be the chance of one of the dice being a six or both being a six.
The union of events A and B is denoted A∪B.
You can find the probability of union using the following formula:
P(A∪B) = P(A) + P(B) – P(A∩B)
The probability of union P(A∪B) is equal to P(A) plus P(B), minus the probability of intersection P(A∩B).
Symmetric Difference
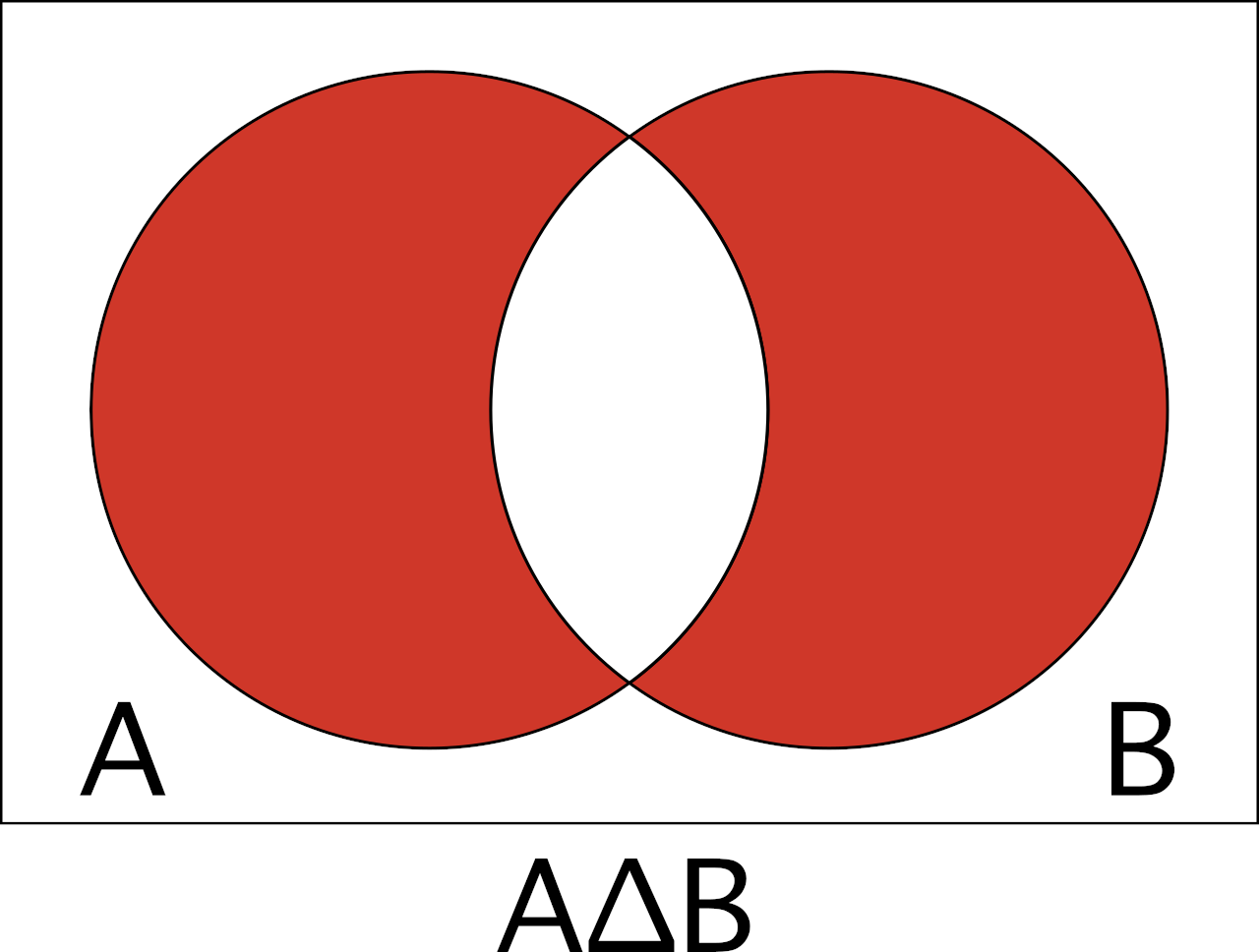
The probability of the symmetric difference is the likelihood that exactly one of the events will occur, but not both. In the dice example, this would be the chance of precisely one of the dice being a six, but not both.
The symmetric difference of events A and B is denoted A∆B.
The symmetric difference is also known as the disjunctive union of two sets, and you can find the probability of it with the following formula:
P(A∆B) = P(A∪B) – P(A∩B)
The probability of the symmetric difference P(A∆B) is equal to union P(A∪B) minus the intersection P(A∩B).
Complement of A
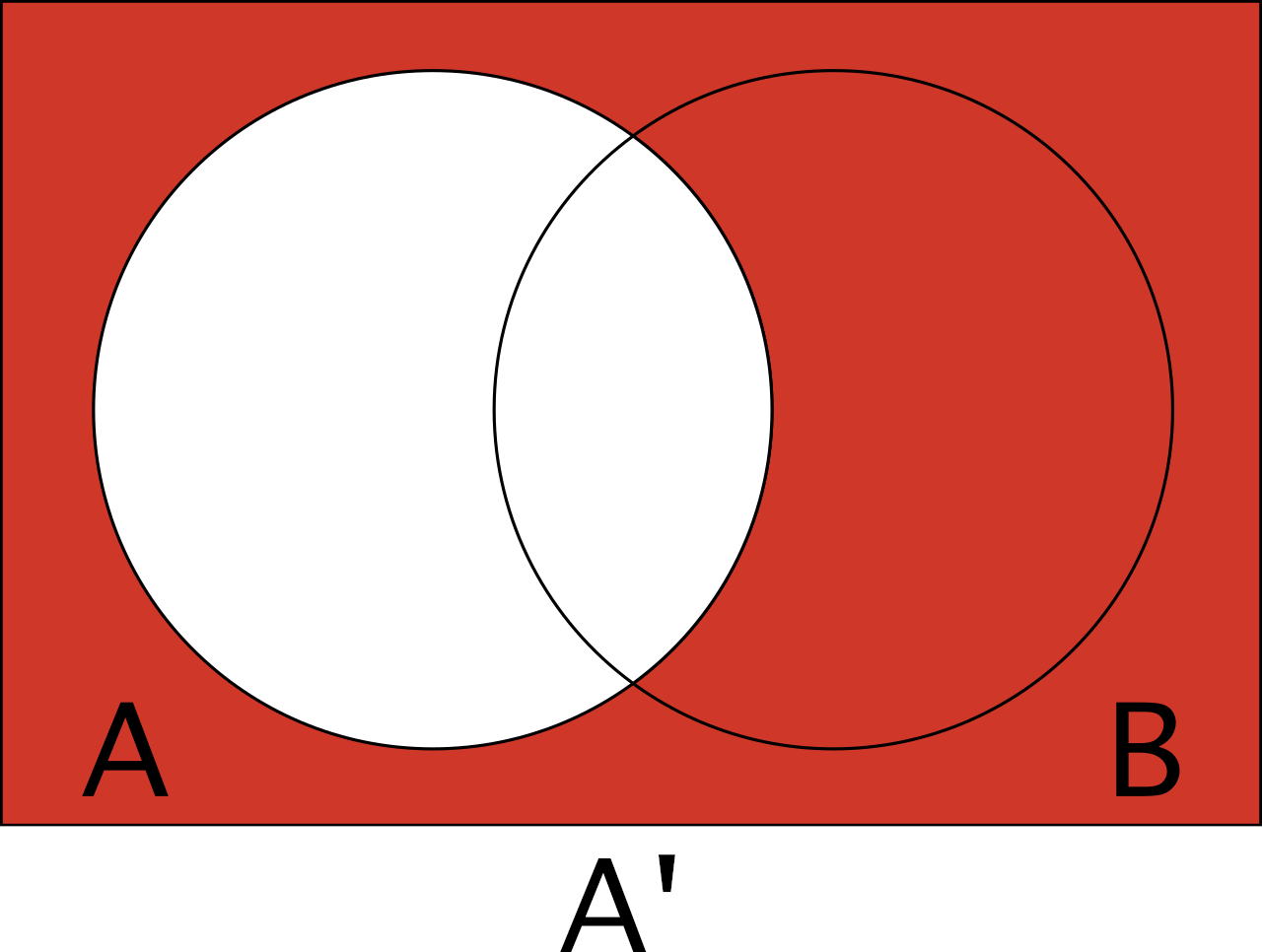
In probability theory, the complement of event A is the likelihood that A does not occur. Thus, the complement of an event is effectively the chance that the event does not happen.
Continuing the dice example, the complement of rolling a six on the first dice is equal to the chance that a six is not rolled on the first dice, even if it’s rolled on the second.
Complement is denoted using an apostrophe (‘). Thus, A’ is the complement of A.
The complement can be found using the formula:
P(A’) = 1 – P(A)
The probability of the complement of A P(A’) is equal to 1 minus P(A).
One of the reasons we use complements in probability analysis is that it is often easier to think about how to calculate quantities in terms of events not occurring.
A well-known example of this is the birthday problem:
In a room of 20 people, what are the chances that two people share a birthday? This problem can be rephrased in terms of complements, what are the chances that no two people in a room of 20 share a birthday?
The first person can be born on any of 365 days, the second person can be born on day 364 of the 365 days year, the second can be born on 363 out of 365 days, and so forth. Hint: you can use our day of the year calendar to find what day your birthday is on.
If you multiply these 365/365 × 364/365 × … × 345/365, then you get 0.55. This implies that in a room full of 20 people, there is a 1 – 0.55 = 0.45 probability that two people will share a birthday. This is much higher than most people would think!
Complement of A∪B
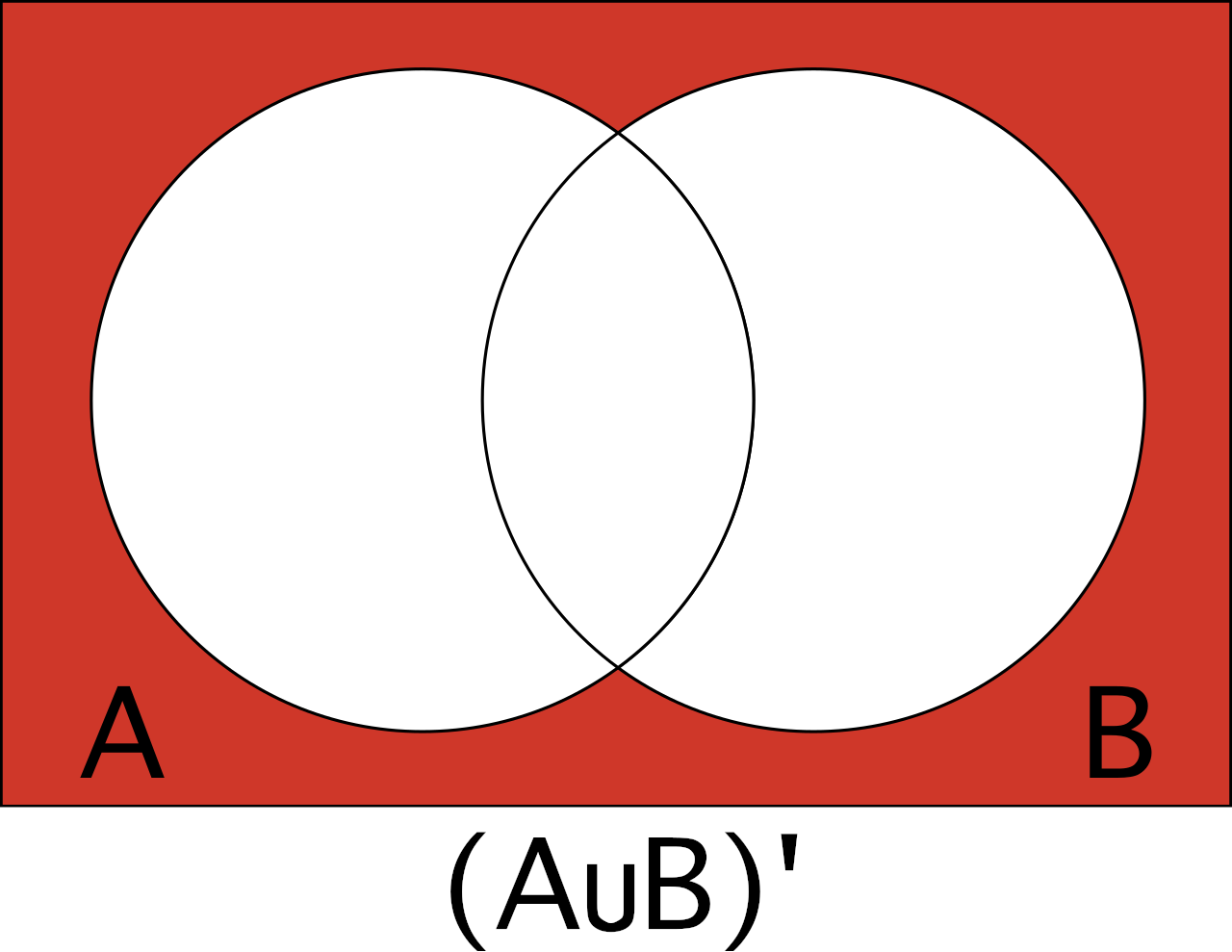
The complement of the union of two events, or (A∪B)’, is the likelihood that neither event A nor event B will occur. In the dice example, this is the likelihood that neither dice is a six when rolling two dice.
P((A∪B)’) can be found using the formula:
P((A∪B)’) = 1 – P(A∪B)
The probability of the complement of A union B P((A∪B)’) occurring is equal to 1 minus the chance of A union B PA∪B).
How to Find the Probability For a Series of Events
Sometimes, you want to find the probability of an outcome occurring in a series of events. For instance, if rolling dice three times, what is the likelihood of rolling a six at least one time?
The formulas below define the probabilities of the outcome occurring at least once, every time, or never during the series.
Event Occurring at Least Once
P(A occurs at least once) = 1 – (1 – P(A))n
The probability of event A occurring at least once in the series of n attempts is equal to 1 minus 1 minus the probability of event A to the nth power.
Event Occurring Every Time
P(A occurs every time) = P(A)n
The probability of event A occurring every time in the series of n attempts is equal to the probability of event A to the nth power.
Event Never Occurring
P(A never occurs) = (1 – P(A))n
The probability of event A never occurring in the series of n attempts is equal to 1 minus the probability of event A to the nth power.
How to Find the Probability For Conditional Events
So far, the formulas for single and series events have assumed the events are independent. Events are independent if one event happening does not have any impact on the probability of the other event occurring.
In the example of rolling the dice, the probability of rolling the dice and getting a six is 1/6, and the probability of rolling a six on the second roll is also 1/6. The probability of rolling a six is always 1/6 for standard dice.
However, consider the deck of cards; the probability of drawing a king from the deck is 4/52, since there are 4 kings and 52 total cards. Let’s say you draw a card that is not a king; what is the probability of drawing a king on the second draw, assuming you did not replace the first card to the deck?
The odds of drawing a king are reduced on the second draw to 4/51, since there are 4 kings and 51 total cards remaining. This is a conditional probability.
You can use Bayes’ theorem to calculate a conditional probability:
P(A|B) = P(B|A) × P(A) / P(B)
Bayes’ theorem states that the probability of event A given that event B also occurs is equal to the probability of event B given that event A also occurs times the probability of event A divided by the probability of event B.
We hope this demystifies some of the probability equations used in statistics. When in doubt, try the calculator above to see what the chances of your outcomes are!
Try our p-value calculator to calculate probabilities of a value drawn from a distribution.
Frequently Asked Questions
Why is probability important?
Probability is important because it gives a way of quantifying the chances of something happening. This allows us to make decisions when outcomes are uncertain. It also gives us a way of understanding the chances of complicated events where intuitions may not be very reliable.
Does probability mean possibility?
Probability is the likelihood or possibility of an event or outcome occurring. So yes, probability can mean possibility.
Is probability always accurate?
You cannot predict what will happen with absolute certainty; however, using probability, you can calculate the likelihood that something will happen given some assumptions about how the world works. The probability of estimates are only as good as your model.
How do you know whether two events are independent?
In practice, it is often hard to know whether two things are related to one another or not; you need to make a judgment call based on your knowledge of the situation and context. The choice matters, however, because the probabilities can radically change if you assume that events are related or not.
As an example, many casinos have rules about gamblers counting cards. By assuming past hands influence future hands, card counters are assuming non-independence. If they count correctly, card counters can only play hands where their odds of winning are very favorable. Gamblers who do not count cards will perceive very different probabilities, and more often than not lose to the card counters.



