Combination Calculator
Enter the total number of objects and the sample size to calculate the possible combinations with the nCr calculator below.
Result:
Number of Combinations C(n,r)
Number of Permutations P(n,r)
On this page:
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
Brian specializes in political science and statistics with several advanced degrees from Harvard.
Bailey is an experienced educator and specializes in K-12 math and science. She holds a Master's degree in professional education and holds several teaching certifications.
How to Calculate Combinations
Combinations are a set of items from a larger collection without regard to the order of the items in the set.
Lottery tickets are a common example to demonstrate what combinations are. Each ticket represents a combination of numbers from a larger set of possible numbers. If order matters, then one is interested in permutations (see below), but not combinations.
Once you know the total number of combinations, then you can calculate the probability of winning. This is actually the basis for calculating probabilities in a binomial distribution, which might track the total number of heads in a series of coin flips.
If you only care about the total, then order does not matter, and so H-H-T is an equivalent outcome to H-T-H.
The calculator above finds the number of possible combinations of elements in a collection. Of course, you can also use a formula the calculate them as well.
The number of possible combinations of objects n in a sample of r elements are often expressed as nCr or n choose r. In formulas, combinations are commonly denoted like this:
Combination Formula
The nCr formula defines the number of possible combinations of r elements in a collection of n total items.
C(n,r) = n! / r!(n – r)!
Thus, the number of possible combinations of r items in a set of n items is equal to n factorial divided by r factorial times n minus r factorial.
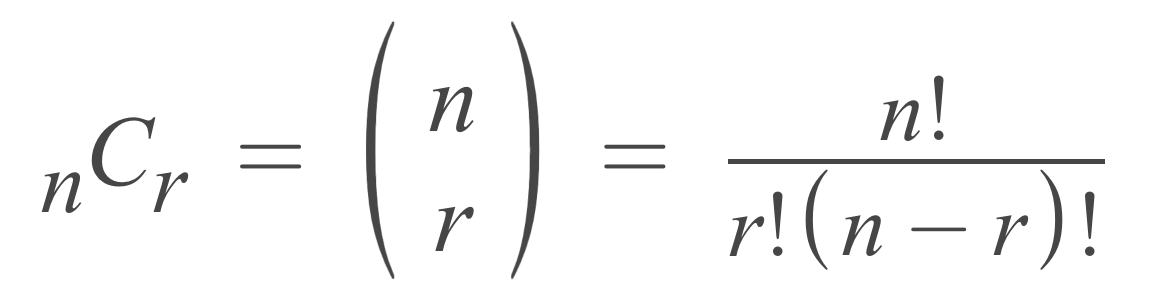
N Choose K
Combinations are also sometimes referred to as n choose k, where n is the total number of items and k is the number of items in the sample. Thus, the number of combinations is equal to the number of ways you can choose k items from a set of n total items.
N Choose K Formula
The n choose k formula is nearly identical to the combinations formula above, but the number of items in the sample is denoted k, and the total number of objects is denoted n.
C(n,k) = n! / k!(n – k)!
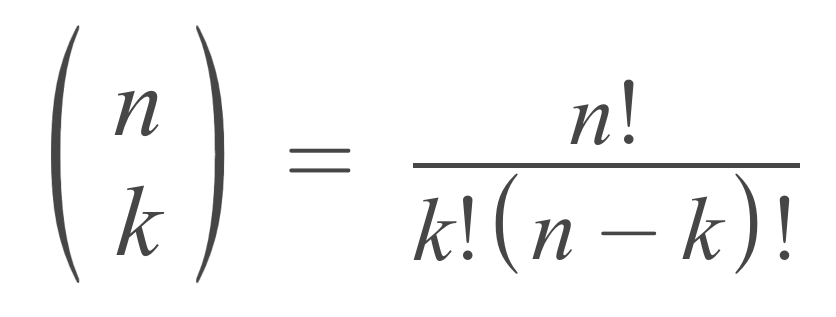
Combinations with Repetitions
To this point, the combinations discussed have not allowed any repetition in the sample, and the assumption has been that each element in the sample is unique. But what if you want to allow for repetitions?
For example, let’s say you have the following fruits: apple, banana, orange, watermelon, and mango. If you’re choosing three of these fruits for snacks throughout the day, it’s possible that you might want to have the same fruit more than once.
A sample of three fruits might be unique (apple, banana, orange) or might include repetitions (apple, apple, banana) or even (apple, apple, apple). The formula to calculate the number of combinations when allowing for repetitions in the sample is a little different.
Combinations with Repetitions Formula
The following formula defines the number of possible combinations with repetitions of r items in a collection of n total items.
C(n + r − 1, r) = (n + r – 1)! / r!(n – 1)!
The number of possible combinations with repetitions of r items in a set of n items is equal to n plus r minus 1 factorial, divided by r factorial times n minus 1 factorial.
Combinations vs. Permutations
Combinations are very similar to permutations with one key difference: the number of permutations is the number of ways to choose r objects in a set of n objects in a unique order. Thus, with permutations, the order of the objects in the set is important.
In most cases, there will be more possible permutations of objects in a set than combinations because each different order of the items is considered a different permutation. With combinations, the order is irrelevant, and elements in different orders are considered the same combination, hence the number of combinations should be smaller.
A good way to illustrate the difference is with a simple combination lock. A lock may have three numbers in the combination, but the order of these numbers is very important. If you enter the three numbers in the correct order the lock will open, but entering them out of order will not unlock the lock.
So, to find the possible sequences of numbers to open the lock, you actually want to find the permutations of three numbers.
For example, see the combinations and permutations of two letters in a set three letters {A, B, C}.
Combinations (3)
(A, B)
(A, C)
(B, C)
Permutations (6)
(A, B)
(B, A)
(A, C)
(C, A)
(B, C)
(C, B)
Thus, for a sample of two objects in a total number of three objects, there are three combinations and six permutations.
Permutations Formula
The nPr formula below states how to calculate permutations:
P(n,r) = n! / (n – r)!
Thus the number of possible permutations of r items in a set of n items is equal to n factorial divided by n minus r factorial.
Note the similarities in the two formulas. The main difference is that the combination formula divides by the factorial of the number of items selected, which is to account for the number of different ways to arrange those item and still produce the same combination.
Frequently Asked Questions
How do you know when to use combinations?
Mathematical combinations, denoted as n choose k or C(n, k), are used in various mathematical and combinatorial scenarios to provide ways of selecting k items from a set of n distinct items, disregarding their order.
They find applications in probability, counting possibilities, solving combinatorial problems, poker hand probabilities, lottery odds calculations, and algebraic expressions like binomial expansions.
Combinations are most useful when you need to count or calculate possibilities without considering item order, while permutations are more suitable when order matters, and the choice depends on the specific problem at hand.
What do n and k mean in combinations?
In combinations, n and k are variables that represent specific values:
n (often referred to as “the total number of items” or “the size of the set”): This represents the total number of distinct items or elements in a set from which you want to choose a subset. In other words, n is the total population or the total pool of items you’re selecting from.
k (often referred to as “the number of items to choose” or “the size of the subset”): This represents the number of items you want to select or choose from the total population n. In other words, k is the size of the subset you’re interested in.
Why does n choose 0 equal 1?
In combinatorics, n choose k, or C(n, k), signifies the ways to select k items from a set of n without considering their order.
When you compute n choose 0, you’re essentially determining how many ways you can select zero items from a set of n. This gives a result of 1 because choosing nothing is a one option.