Angle of Depression Calculator
Calculate the angle of depression by entering the vertical drop (rise) and horizontal distance (run) below.
Angle of Depression:
| Degrees: | |
| Radians: |
On this page:
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
Pateakia has worked in education for 15 years and has three degrees, including a PhD, Master's degree, and Bachelor's degree. She specializes in mathematics.
How to Calculate the Angle of Depression
The angle of depression is the negative, or downward, angle of a line of sight from an observer to an object. Imagine you are an airline pilot looking down at a runway while landing an airplane; the angle of depression is the angle your head needs to tilt to see the runway on the ground in the distance in front of you.
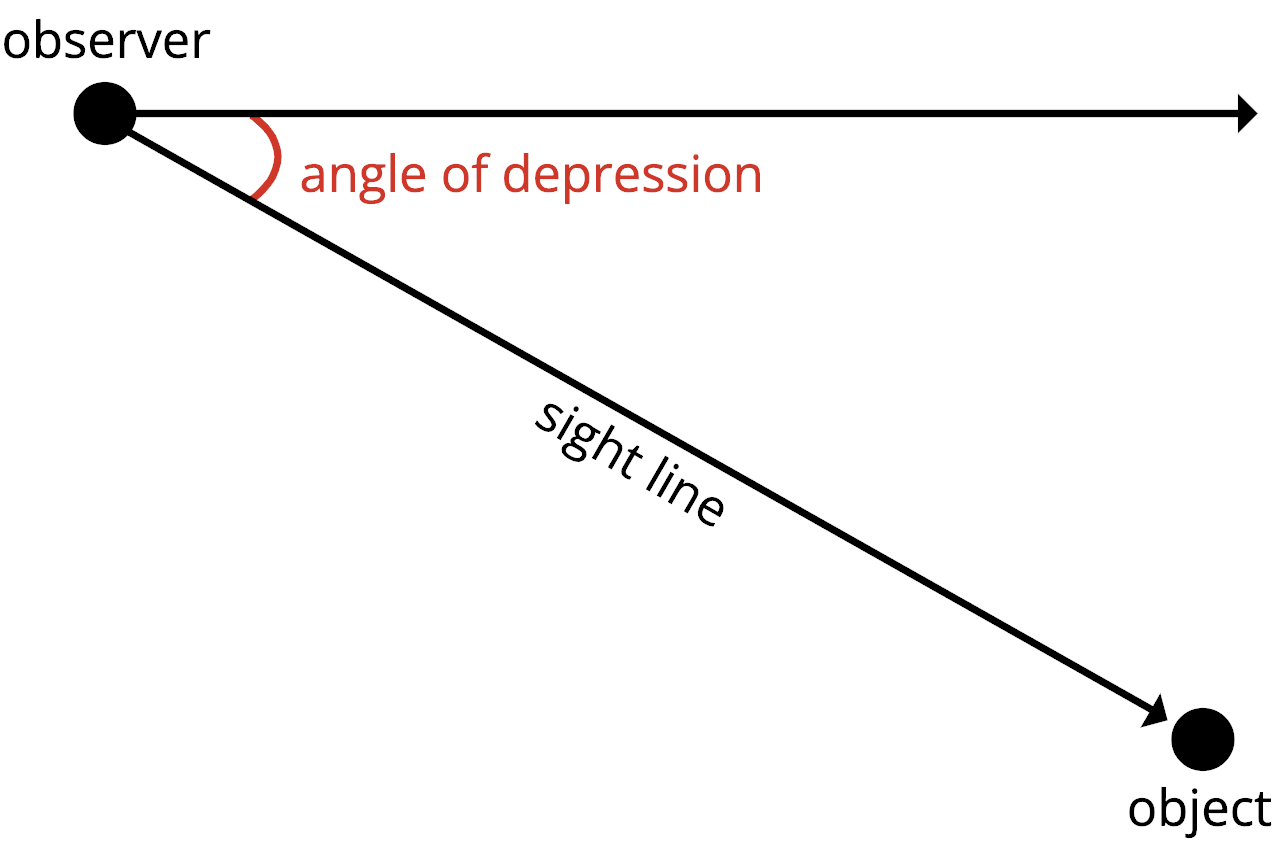
You can calculate the angle of depression using the same methods as you would to solve for the angle in a right triangle.
To calculate the angle of depression, set the horizontal baseline as one side and the sight line as the hypotenuse of a right triangle, then solve the angle between the sides using the appropriate trigonometry formula.
Angle of Depression Formula
The formula to calculate the angle of depression is the same formula used to calculate the angle of elevation:
tan(÷) = opposite ÷ adjacent
The tangent of the angle ÷ is equal to the length of the opposite side divided by the length of the adjacent side.
If you substitute the vertical height for the opposite side and the horizontal distance of the object for the adjacent side into this formula, you can calculate the angle of depression.
Note that for an angle of depression, the rise will actually be negative, but you will need to use the positive value for this equation.
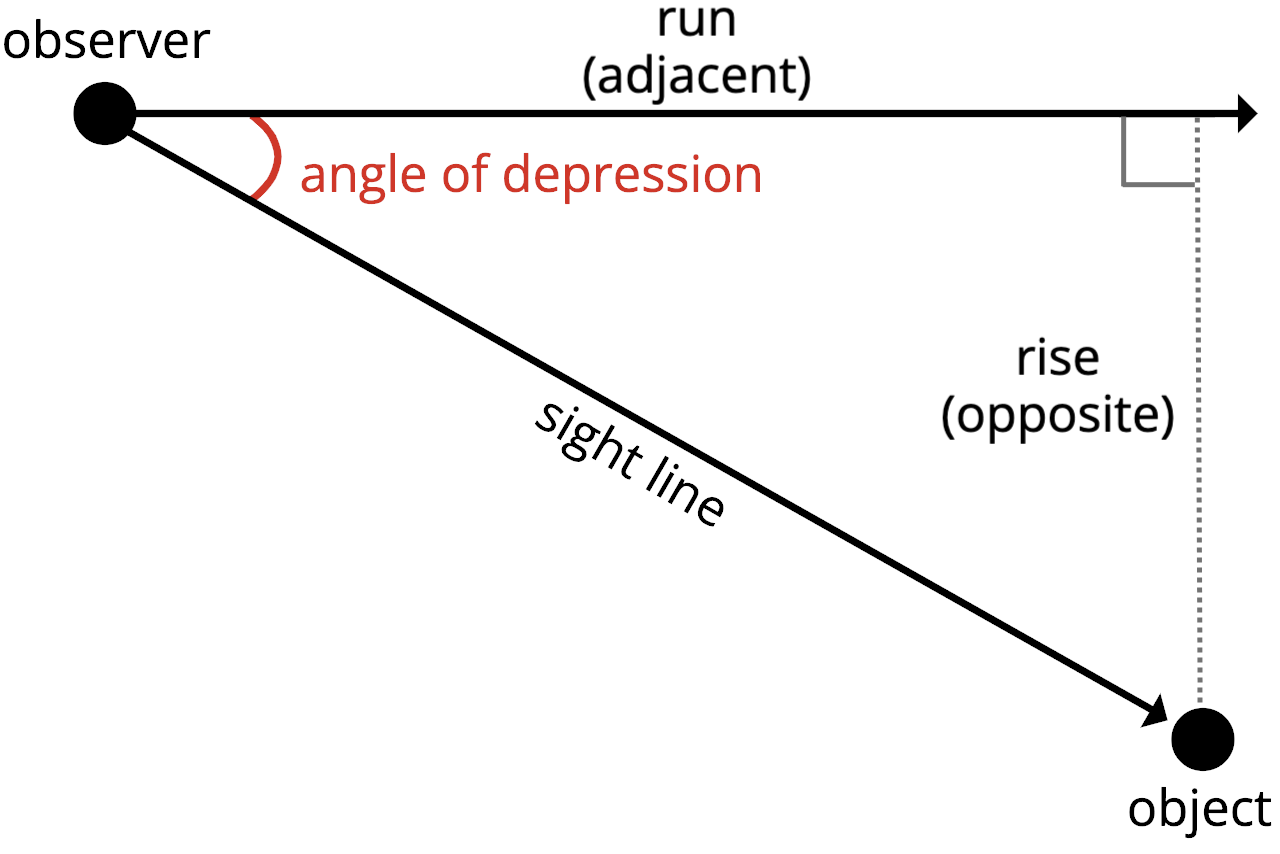
Rewriting the Formula
The angle of depression equation becomes:
tan(angle of depression) = rise ÷ run
The tangent of the angle of depression is equal to the vertical height (rise) divided by the horizontal distance (run). Thus, the slope of the sight line is equal to the tangent of the angle.
Using Inverse Tangent
Since the formula above gives us the result as the tangent of the angle, you can use the inverse tangent function to calculate the angle of depression:
angle of depression = atan(rise ÷ run)
Therefore, the angle of depression is equal to the inverse tangent of the vertical height (rise) divided by the horizontal distance (run).
You can learn more about this with our elevation grade calculator.
Frequently Asked Questions
How do you find the depth of an object using the angle of depression?
To find the depth h of an object using the angle of depression θ, you’ll need to know the distance between the observer and the object d. You can calculate the depth of the object using the following formula:
h = d × tan(θ)
Note: the result for depth h will be a positive value, so be sure to flip it negative for the final result.
How do you calculate distance using the angle of depression?
To calculate the distance d to an object of depth h using the angle of depression θ, you can use the formula:
d = h ÷ tan(θ)
The distance d is equal to the depth h divided by the tangent of the angle of depression θ.
What is the maximum angle of depression?
The maximum angle of depression occurs when the object is directly below the observer. When this is the case, the angle of depression is 90 degrees, which is the maximum value it can have.