Vertex Form Calculator
Convert the formula of a parabola from standard to vertex form or vertex to standard form using the vertex formula calculator below.
Results:
Vertex Form
Standard Form
Vertex
Y-interept
Standard Form
Vertex Form
Vertex
Y-interept
On this page:
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
Ethan has a PhD in astrophysics and is currently a satellite imaging scientist. He specializes in math, science, and astrophysics.
How to Convert Standard Form to Vertex Form
A parabola is the graph of a quadratic equation, which is an equation that has its variable, usually x, raised to the power of 2, which is also the largest exponent on that variable seen in the equation. (For example, y = x² + x is a quadratic equation, but y = x³ + x² is not.)
The standard form of a quadratic equation is given by:
y = ax² + bx + c
where a, b, and c are constants. This is the standard form equation, or just standard form for a quadratic equation. Be careful not to confuse this with standard form in the context of scientific notation, which is a very different thing.
Every parabola has either a minimum (upwards opening parabola) or a maximum point (downwards opening parabola), which is known as the vertex. More formally, the vertex is the extremal value of the quadratic curve.
So you might be wondering how to find vertex form from the standard form equation above. The vertex form of a quadratic equation is given by:
y = a(x – h)² + k
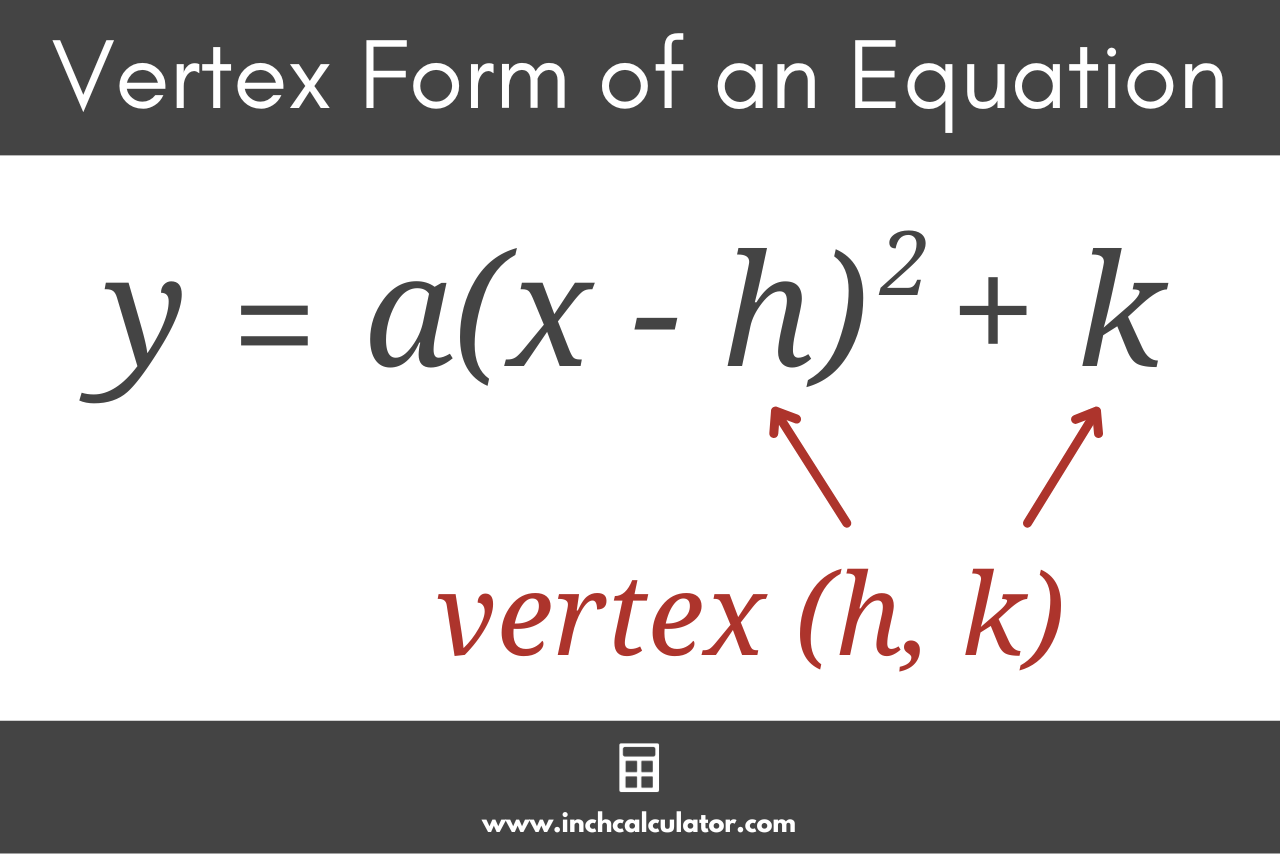
Follow these few simple steps to find out how to convert to vertex form.
Step One: Find the Vertex
The vertex is denoted P(h, k), where h is the x-coordinate and k is the y-coordinate. You can find the vertex given the standard form using the following formulas.
h = -b / 2a
k = c – b² / 4a
Thus, h is equal to negative b divided by 2 times a, and k is equal to c minus b squared divided by 4 times a.
Step Two: Use the Vertex Form Equation
Given the coordinates of the vertex and the standard form equation, you can express a parabola in vertex form using the following equation:
y = a(x – h)² + k
For example, let’s convert the equation y = 4x² + 3x + 1 from standard form to vertex form.
Start by finding h.
h = -3 / 2 × 4
h = -3 / 8
h = -0.375
Then find k.
k = 1 – 3² / 4 × 4
k = 1 – 9 / 16
k = 1 – 0.5625
k = 0.4375
Then substitute these values into the vertex form formula, and the quadratic equation in vertex form is:
y = 4(x + 0.375)² + 0.4375
How to Convert Vertex Form to Standard Form
After learning how to convert standard form to vertex form, it’s logical to ask, how do we convert from vertex form to standard form? Recall from above that vertex form for a parabola looks like this.
y = ax² + bx + c
You can use the same formulas above that were used to convert standard form to vertex form to find the values h and k given the standard form of a parabola, except this time, we solve them for b and c, respectively:
b = -2ah
c = ah² + k
So, value b is equal to -2 times a times h, and c is equal to a times h squared plus k.
Then, using these values, write the equation in standard form.
y = ax² + bx + c
For example, let’s convert the equation y = 3(x + 2)² + 1 from vertex form to standard form.
Start by finding b.
b = -2 × 3 × -2
b = 12
Then find c.
c = 3 × -2² + 1
c = 3 × 4 + 1
c = 13
Then substitute these values in the standard form equation:
y = 3x² + 12x + 13
Frequently Asked Questions
When do you use vertex form?
You use vertex form when you want to represent a quadratic equation in a form where it’s easy to identify its vertex. This is very helpful when plotting the parabola because you already know the coordinates of the vertex just by looking at the equation.
What does vertex form tell you?
Vertex form not only tells you the equation of a parabola just like standard form, but it also quickly tells you the coordinates of its vertex.
Can you find vertex form using two points?
Finding the equation of a parabola in vertex form using only two points is technically possible, although there are actually an infinite number of parabolas that can be fit to only two points. One would need at least 3 points to find the equation of a specific parabola in vertex form.