Scientific Notation Calculator and Converter
Convert a number to scientific notation, E notation, or engineering notation or vice-versa using the scientific notation calculator.
Solution:
Scientific Notation
E Notation
Engineering Notation
Decimal Notation
On this page:
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
Ethan has a PhD in astrophysics and is currently a satellite imaging scientist. He specializes in math, science, and astrophysics.
How to Convert Scientific Notation to Decimal Form
Scientific notation, also called standard form, represents very large numbers or very small numbers in a shorter, more digestible format. Numbers in scientific notation are an expression of a coefficient multiplied by 10 to the nth power.
Here’s an example:
1.5 × 102
The number to the left of the multiplication symbol is the coefficient, sometimes also called the mantissa. These are the significant digits in the number.
The number of digits in the coefficient will vary depending on how many significant figures are in the number. Use our significant figures calculator to find significant figures or round a number to a specified number of significant digits to prepare for conversion to scientific notation.
Convert Using a Calculator
To convert a number that is currently in scientific notation to decimal notation, evaluate the expression. To do so, multiply the coefficient by ten to the nth power (or check out an even easier solution below).
You can also use our exponent calculator to evaluate the second part of the expression, then multiply the result by the coefficient.
For example, let’s convert 1.5 × 102 to decimal form.
1.5 × 102 = 1.5 × 100
1.5 × 102 = 150
Convert Scientific Notation Without a Calculator
We’ve shown you how to convert a number expressed in scientific notation to a decimal by evaluating, but this becomes more tedious to do manually as the exponent gets larger. There’s an alternate way to convert to decimal without performing explicit multiplication.
If the exponent is positive, move the decimal point in the coefficient to the right one space for each value in the exponent. If the exponent is negative, move the decimal point one space to the left for each value in the exponent.
For instance, if the exponent is two, then move the decimal point to the right two spaces. If the exponent is negative two, then move the decimal point to the left two spaces.
For example, let’s convert 1.5 × 102 to a decimal using this method.
1.5 × 102 = 15.0 × 101
1.5 × 102 = 150 × 100
1.5 × 102 = 150
How to Convert a Decimal to Scientific Notation
Converting a decimal number to scientific notation can be done in a few simple steps.
Step One: Create Initial Expression
First, create an expression with the initial decimal being the coefficient multiplied by 10 to the power of 0.
For example, let’s create the starting scientific notation expression for the decimal 475,000.
475,000 = 475,000 × 100
Step Two: Move the Decimal Point
Now that we have an expression, the second step is to move the decimal point in the coefficient until there is one significant digit to the left of the decimal point. For each space you move the decimal point to the left, increase the exponent by 1.
Continuing the example above, move the decimal point to the left and incrementally increase the exponent.
475,000 = 475,000.0 × 100
475,000 = 47,500.0 × 101
475,000 = 4,750.0 × 102
475,000 = 475.0 × 103
475,000 = 47.5 × 104
475,000 = 4.75 × 105
What About Numbers Less Than One?
The method above works for large numbers, but as mentioned above, the method for handling numbers smaller than one is a bit different.
Instead of moving the decimal point to the left in the coefficient, the decimal point needs to be moved to the right until one non-zero significant digit is to the left of the decimal point. Because the number is getting larger, we need to decrement a number from the exponent every time the decimal point is moved.
For example, let’s convert 0.00025 to scientific notation.
0.00025 = 0.00025 × 100
0.00025 = 0.0025 × 10-1
0.00025 = 0.025 × 10-2
0.00025 = 0.25 × 10-3
0.00025 = 2.5 × 10-4
How to Use Exponential Notation
Exponential notation, or E notation, is another form of scientific notation where the “× 10” part of the equation is replaced with an “e” or “e+” if the exponent is positive and “e-” if the exponent is negative.
The “E” in E notation stands for exponential. This form is also commonly referred to as scientific E notation.
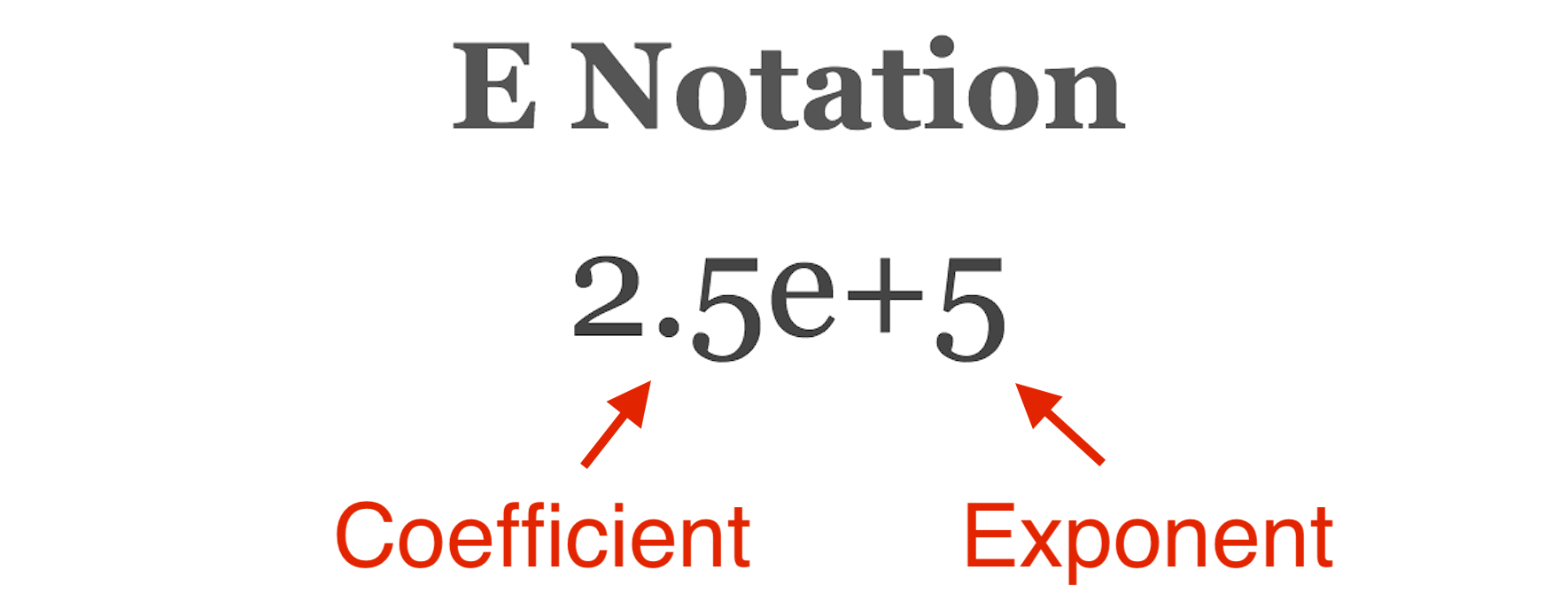
For example, let’s represent 1.5 × 102 and 6.8 x 10-7 in E notation.
1.5 × 102 = 1.5e+2
6.8 × 10-7 = 6.8e-7
How to Convert to Engineering Notation
Not to be confused with E notation, engineering notation is an alternate form of scientific notation where the exponent is a multiple of 3.
To convert scientific notation to engineering notation, move the decimal point in the coefficient to the right and reduce the exponent until the exponent is a multiple of 3.
For example, let’s represent 1.5 × 105 in engineering notation.
1.5 × 105 = 15.0 × 104
1.5 × 105 = 150.0 × 103
Scientific Notation and Decimal Equivalents
| Decimal Number | Scientific Notation | E Notation | Engineering Notation |
|---|---|---|---|
| 1 | 1 × 100 | 1E+0 | 1 × 100 |
| 1,000 | 1 × 103 | 1E+3 | 1 × 103 |
| 72,000 | 7.2 × 104 | 7.2E+4 | 72 × 103 |
| 1,349.12 | 1.34912 × 103 | 1.34912E+3 | 1.34912 × 103 |
| 0.000000435 | 4.35 × 10-7 | 4.35E-7 | 435 × 10-9 |
| -7,500 | -7.5 × 103 | -7.5E+3 | -7.5 × 103 |
| -0.00005234 | -5.234 × 10-5 | -5.234E-5 | -52.34 × 10-6 |
Frequently Asked Questions
Why is scientific notation important?
Scientific notation is important because it allows one to make very large or very small numbers much more readable and manageable. They also make calculations easier because multiplying two very large numbers in scientific notation together, for example, would consist of simply multiplying the coefficients together and then adding the exponents.
As an example, multiply 2 × 104 and 3 × 106:
(2 × 104) × (3 × 106) = 6 × 1010
When should scientific notation be used?
Scientific notation should be used when working with very large or very small numbers, and converting to this format would make the numbers much easier to work with.
Are scientific notation and standard form the same?
Yes, scientific notation and standard form are two different names for the same mathematical format.
How are scientific notation and exponential notation different?
Scientific notation uses a coefficient, a multiplication sign, and a ten to some exponent, whereas exponential notation uses a coefficient, the letter e, and the exponent.
For example, 3 × 104 = 3e4
You might also like our numbers to words converter for transforming numbers in scientific notation to word form.
Visual Guide to Convert to Scientific Notation
The infographic below demonstrates visually how to convert a number to scientific notation.
