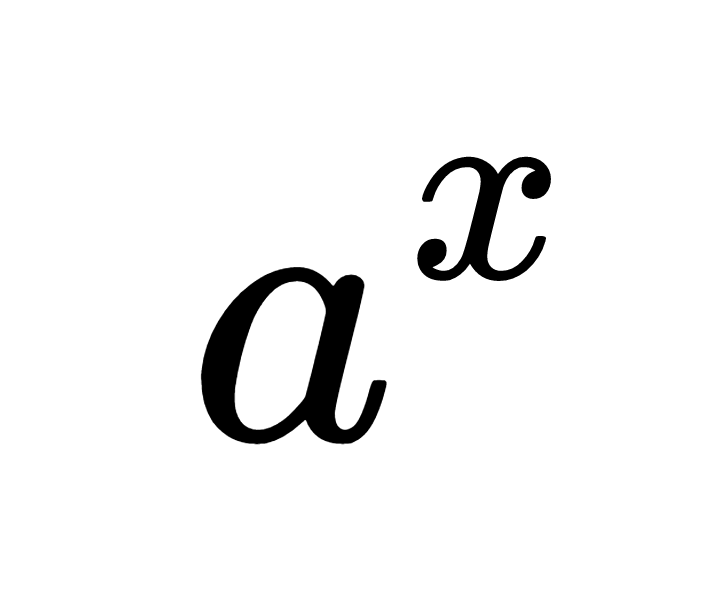Exponent Calculator
Enter the base and exponent to calculate the result below.
ax = ?
Results:
On this page:
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
How to Calculate an Exponent
An exponent is the number of times the base value should be multiplied by itself. To calculate a number raised to an exponent, multiply the number by itself for each value of the exponent.
So 52 is the same as 5 × 5 and 53 is the same as 5 × 5 × 5.
Calculating an exponent is also sometimes referred to as raising a number to the nth power.
For example, calculate the result of 84.
84 = 8 × 8 × 8 × 8
84 = 4,096
Thus, 84, or 8 to the 4th power, is equal to 8 times 8 times 8 times 8, which is equal to 4,096.
How to Calculate a Negative Exponent
What do you do if the exponent is negative? For a negative exponent rather than multiplying the number by itself the number of times for the exponent, you divide the number by itself, starting with 1.
So 5-2 is the same as 1 ÷ 5 ÷ 5 and 5-3 is the same as 1 ÷5 ÷ 5 ÷ 5.
Negative exponents are often expressed as 1 over the base with a positive exponent.
5-2 = 1 / 52
For example, calculate the result of 84.
8-4 = 1 / 84
8-4 = 1 / 8 × 8 × 8 × 8
8-4 = 1 / 4,096
8-4 = 0.000244140625
Thus, 8-4 is equal to 0.000244140625.
Special Exponent Rules
There are some special rules with exponents that are important to remember.
When the exponent is 1, the result of raising a base to the exponent will always be equal to the base.
a1 = a
When the exponent is 0, the result of raising a base to the exponent will always be equal to 1.
a0 = 1
When the exponent is 2 you can also say that the base value is squared. When the exponent is 3 you can say that the base value is cubed.
The calculator above will handle these special cases along with negative exponents to solve the answer.
Exponent Table
| Powers of Two | Powers of Three | Powers of Four | Powers of Five |
|---|---|---|---|
| 20 = 1 | 30 = 1 | 40 = 1 | 50 = 1 |
| 21 = 2 | 31 = 3 | 41 = 4 | 51 = 5 |
| 22 = 4 | 32 = 9 | 42 = 16 | 52 = 25 |
| 23 = 8 | 33 = 27 | 43 = 64 | 53 = 125 |
| 24 = 16 | 34 = 81 | 44 = 256 | 54 = 625 |
| 25 = 32 | 35 = 243 | 45 = 1024 | 55 = 3125 |
| 26 = 64 | 36 = 729 | 46 = 4096 | 56 = 15625 |
| 27 = 128 | 37 = 2187 | 47 = 16384 | 57 = 78125 |
| 28 = 256 | 38 = 6561 | 48 = 65536 | 58 = 390625 |
| 29 = 512 | 39 = 19683 | 49 = 262144 | 59 = 1953125 |
| 210 = 1024 | 310 = 59049 | 410 = 1048576 | 510 = 9765625 |
