Quadratic Formula Calculator (with Steps)

Enter the coefficients that form a quadratic equation to solve for x using the quadratic formula.

Have a Question or Feedback?

Result:

x=-0.333333

x=-0.5

Solution

6x²+5x+1=0

To solve, use the quadratic formula

x=-b ± b² - 4ac2a

Substitute your values for a, b, & c and solve

x=-5 ± 5² - 4·6·12·6

x=-5 ± 25 - 2412

x=-5 ± 112

Next, solve the radical

x=-5 ± 112

Then, reduce the problem

x=-512±112

x=-0.333333

x=-0.5

Learn how we calculated this below

scroll down

How to Use the Quadratic Formula

The quadratic formula can be used to calculate the solution for x in a quadratic equation. A quadratic equation is a second-degree polynomial equation.

The quadratic formula uses numerical coefficients from a quadratic equation to allow you to solve for the value of x. In the quadratic formula, a is the quadratic coefficient, b is the linear coefficient, and c is the constant.

Graphic showing the quadratic formula used to solve quadratic equations

You can solve a quadratic equation of the form ax² + bx + c = 0 using a quadratic equation solver like the one above or using the quadratic formula:

x = \frac{-b \pm \sqrt{b^{2}-4ac}}{2a}

Thus, the value of x is equal to -b plus or minus the square root of b squared minus 4 times a times c over 2 times a, where a is not equal to 0.

When the discriminant b² – 4ac is equal to 0 then there will be a single solution for x, otherwise, there will be two possible solutions for x.

To use the quadratic formula, replace a, b, and c with the coefficients from the ax² + bx + c = 0 equation, then solve.

The value of a cannot be equal to zero as that would indicate the formula is missing the quadratic term x², which would mean it’s not a quadratic equation.

Let’s solve the equation 3x² + 8x + 4 = 0 using the quadratic formula as an example.

Start by substituting the coefficients into the formula:

x = \frac{-8 \pm \sqrt{8^{2}-4 \cdot 3 \cdot 4}}{2 \cdot 3}

Begin solving the equation:

x = \frac{-8 \pm \sqrt{64-48}}{6}

x = \frac{-8 \pm \sqrt{16}}{6}

x = \frac{-8 \pm 4}{6}

Next, simplify the fraction:

x = \frac{-8}{6} \pm \frac{4}{6}

x = \frac{-4}{3} \pm \frac{2}{3}

Thus, there are two solutions for x:

x = \frac{-4}{3}+ \frac{2}{3} = -\frac{2}{3}

x = \frac{-4}{3}- \frac{2}{3} = -\frac{6}{3} = -2

Why Are There Two Solutions to the Quadratic Equation?

When y = 0 in a quadratic equation, deriving the solution for x results in the quadratic formula. During the derivation, one must take the square root in order to isolate x (recall √x² = x).

However, whenever one takes the square root of a positive value, there are always two possible answers, a positive answer and a negative answer. That is because two positive numbers multiplied together results in a positive number, but two negative numbers multiplied together also results in a positive number.

For example, the square root of 9 is plus or minus 3, because 3 x 3 = 9 and -3 x -3 = 9 as well. Therefore, whenever you take a square root of an expression, it is good practice to write +/- √ to express that there are two possible solutions.

Therefore, because the quadratic formula contains the square root of (b² – 4ac), we must include the plus or minus in front, which results in two possible results for the square root and thus, two possible solutions to the quadratic equation.

The one exception to this rule is if b^2 – 4ac (called the discriminant) equals zero, because the square root of zero only equals zero.

You may be wondering, though, what if the discriminant is less than zero? Can you take the square root of a negative number? The answer is yes, it simply requires the use of imaginary numbers.

The imaginary number, i, is equal to the square root of negative one, √(-1). Therefore, i² = 1. So if we take the square root of -4, for example, we get:

x = \sqrt{-4} = \sqrt{-1} \times \sqrt{4}

x = i \times 2 = 2i

As an example of when you may encounter imaginary numbers, let’s solve 2x² + 2x + 5 = 0 for x, using the quadratic formula. Substituting the coefficients into the equation, we get

x = (-2 \pm \sqrt{2^{2} – 4 \cdot 2 \cdot 5})/2 \cdot 2

x = -2/4 \pm \sqrt{-36}/4

x = -1/2 \pm 6i/4

x = -1/2 \pm 3i/2

Therefore, the solutions to the above equation are

x = -1/2+3i/2

x = -1/2-3i/2

When using imaginary numbers, however, you cannot graph a parabola on an x-y plane like usual. Instead, you can graph it on a Real-Complex plane, but that is a topic beyond the scope of this discussion.

How to Graph a Quadratic Equation

When graphed, the quadratic formula forms a parabola, or a curve in the shape of a U.

Note that smaller values of a form a wider parabolic curve, and larger values of a form a thinner parabola. A negative a value results in an upside-down parabola.

By setting y = 0 in the equation and solving for x, the resulting x values are the x-intercepts where the parabola crosses the x-axis.

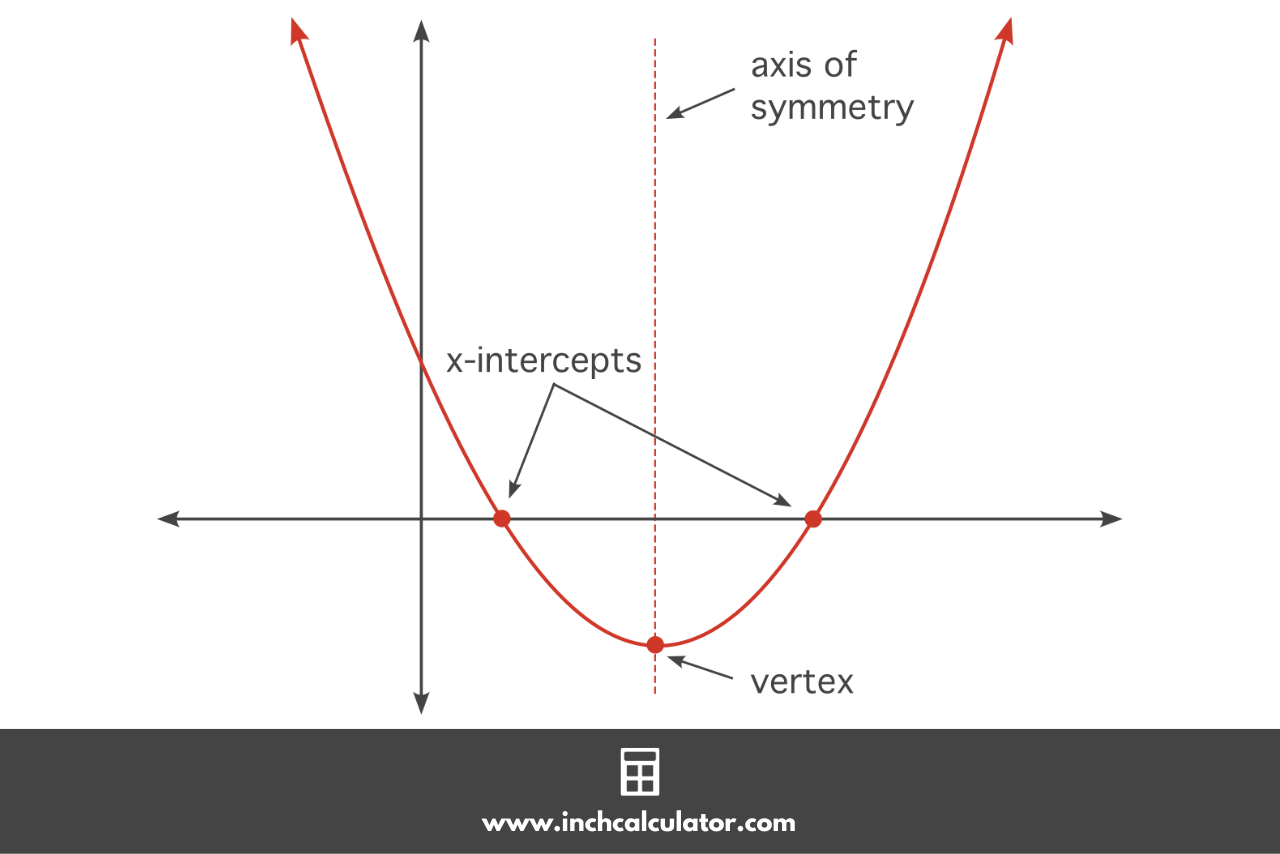
Graph of a quadratic equation showing the x-intercepts, vertex, and axis of symmetry

How to Find the Vertex

The general expression f(x) = ax² + bx + c is known as the standard form of a quadratic equation. But, you can also express a quadratic equation using vertex form.

A quadratic equation expressed in vertex form has the formula:

f(x)=a(x-h)^{2}+k

Where:

h=\frac{-b}{2a}

k=c-\frac{b^{2}}{4a}

The values of h and k in vertex form define the coordinates of the vertex point (h, k).

You might be interested in using our vertex form calculator to convert from standard form to vertex form.

How to Find the Axis of Symmetry

The quadratic equation also defines an axis of symmetry, which is a vertical line at the center of the parabola passing through its vertex. The formula to calculate the axis of symmetry is:

x=\frac{-b}{2a}

Thus, the x coordinate of the axis of symmetry is equal to negative b divided by 2 times a.

Frequently Asked Questions

Why is the quadratic formula important?

The quadratic formula is important because it allows us to solve quadratic equations, which are commonly found in many different disciplines. For example, the quadratic formula is often used to calculate profits, determine areas of construction projects, and the velocity of moving objects.

When is the quadratic formula used?

The quadratic formula is used whenever we want to solve a quadratic equation for the unknown variable.

What are the three quadratic forms?

The three quadratic forms are standard form, factored form, and vertex form.

Standard Form:
y = ax² + bx + c

Factored Form:
y = a(x – r₁)(x – r₂)

Vertex Form:
y = a(x – h)² + k

Quadratic Formula Calculator