Cosecant Calculator – Calculate csc(x)
Find the cosecant of an angle using the csc calculator below. Start by entering the angle in degrees or radians.
On this page:
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
Bailey is an experienced educator and specializes in K-12 math and science. She holds a Master's degree in professional education and holds several teaching certifications.
How to Find the Cosecant of an Angle
In a right triangle, the cosecant of angle α, or csc(α), is the ratio between the opposite side of an angle and the hypotenuse.
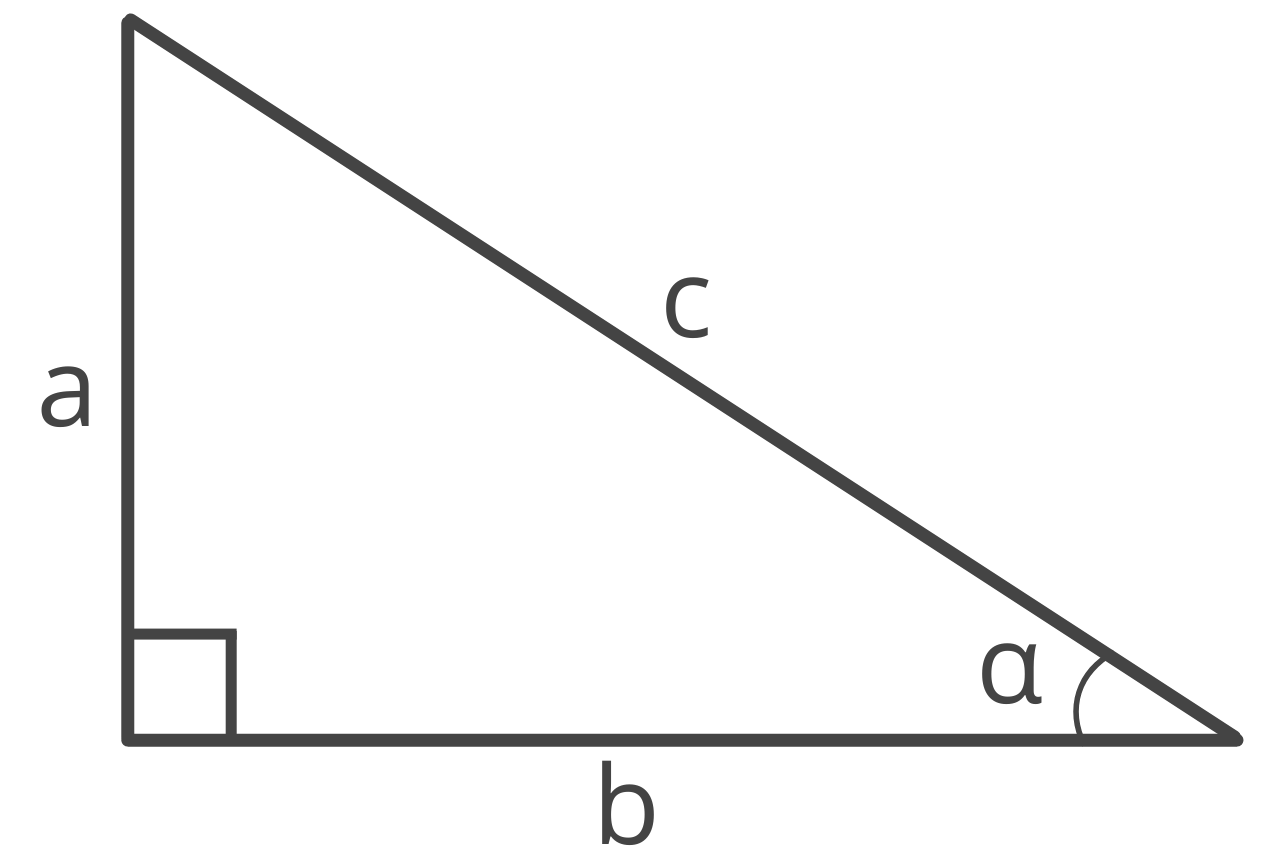
Cosecant is a trigonometric function abbreviated csc. Use the formula below to calculate the cosecant of an angle.
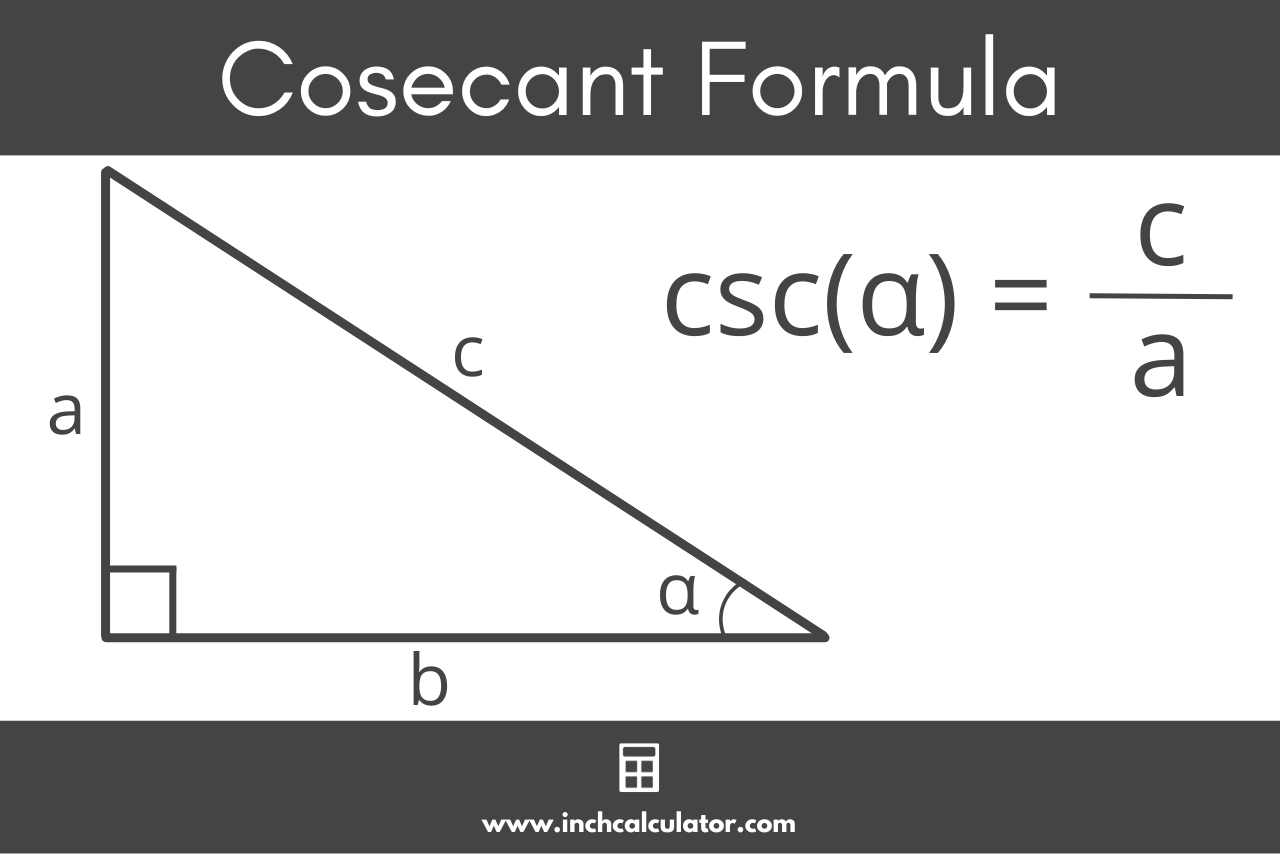
Cosecant Formula
The cosecant formula is:
csc(α) = hypotenuse / opposite = c / a
Thus, the cosecant of angle α in a right triangle is equal to the length of the hypotenuse c divided by the opposite side a.
To find the ratio of csc, simply enter the length of the hypotenuse and opposite side, then simplify.
This formula might look very similar to the formula to calculate sine. That’s because cosecant is the reciprocal of sine.
For example, let’s calculate the cosecant of angle α in a triangle with the length of the hypotenuse equal to 6 and the opposite side equal to 4.
csc(α) = 6 / 4 = 3 / 2
Cosecant vs. Arcsin
Cosecant should not be confused with arcsin, which is the inverse of the sine function. The difference being that cosecant is equal to 1/sin(x), while arcsin is the inverse of the sine function.
csc(x) = 1 / sin(x) = [sin(x)]-1
Whereas,
arcsin(y) = x or sin(y)-1 = x when y = sin(x)
Cosecant Graph
If you graph the cosecant function for every possible angle, it forms a series of repeating U-curves.
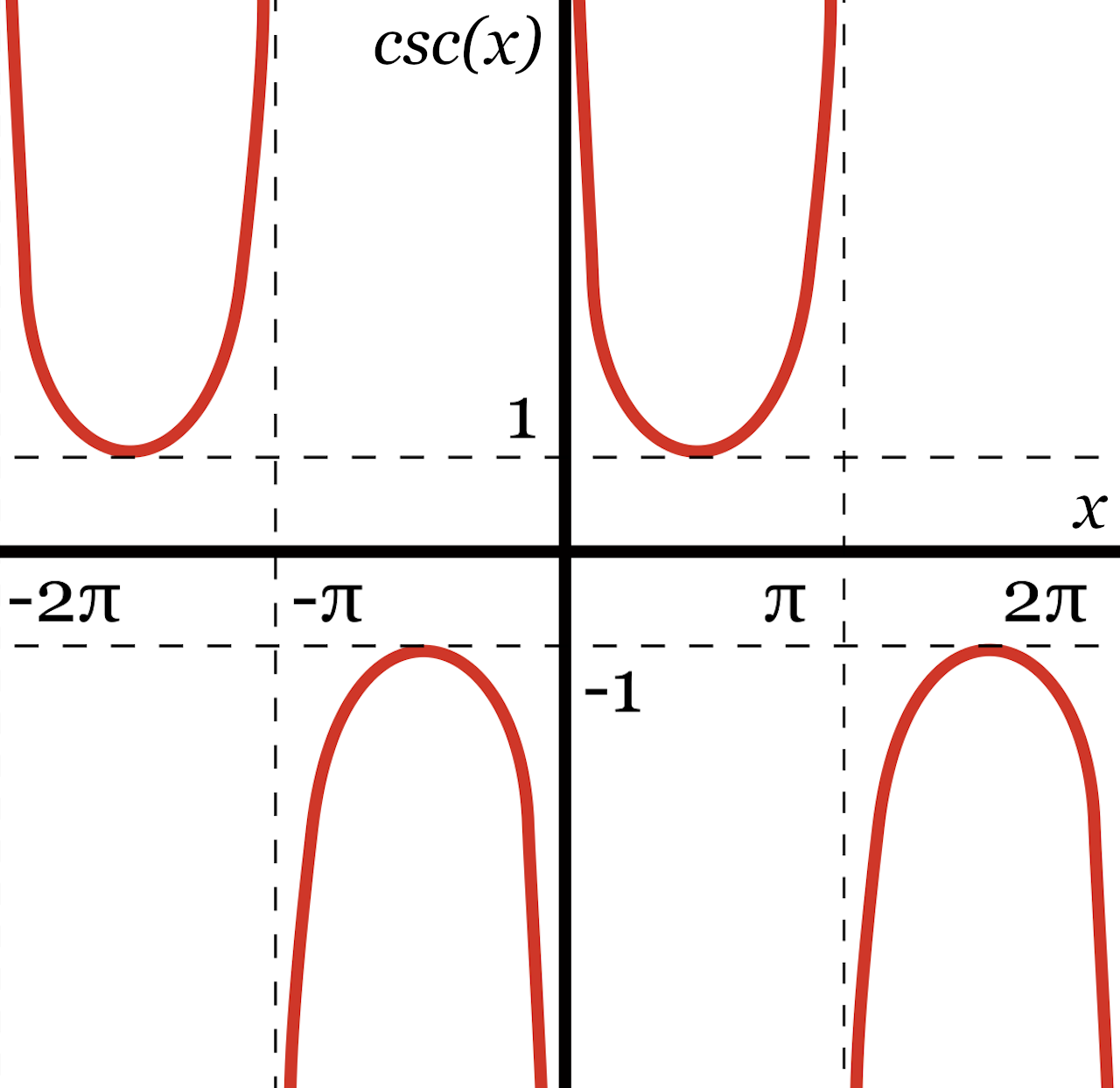
One important property to note in the graph above is that the cosecant of an angle is never in the range of -1 to 1; it’s always smaller than or equal to -1 or larger than or equal to 1.
You’ll also notice that the curves never cross the x-axis.
The cosecant function has asymptotes where the sine function has x-intercepts. This is due to the reciprocal of 0 being undefined. The asymptotes occur every π radians, or 180°. See values in the table below.
The cosecant function continues indefinitely and has a period of 2π. The relative maximum and minimum values occur in each period and are separated by a distance of one period.
Cosecant Table
The table below shows common angles and the csc value for each of them.
| Angle (degrees) | Angle (radians) | Cosecant |
|---|---|---|
| 0° | 0 | undefined |
| 15° | π / 12 | √6 + √2 |
| 30° | π / 6 | 2 |
| 45° | π / 4 | √2 |
| 60° | π / 3 | 2√3 / 3 |
| 75° | 5π / 12 | √6 – √2 |
| 90° | π / 2 | 1 |
| 105° | 7π / 12 | √6 – √2 |
| 120° | 2π / 3 | 2√3 / 3 |
| 135° | 3π / 4 | √2 |
| 150° | 5π / 6 | 2 |
| 165° | 11π / 12 | √6 + √2 |
| 180° | π | undefined |
| 195° | 13π / 12 | -√6 – √2 |
| 210° | 7π / 6 | -2 |
| 225° | 5π / 4 | -√2 |
| 240° | 4π / 3 | –2√3 / 3 |
| 255° | 17π / 12 | √2 – √6 |
| 270° | 3π / 2 | -1 |
| 285° | 19π / 12 | √2 – √6 |
| 300° | 5π / 3 | –2√3 / 3 |
| 315° | 7π / 4 | -√2 |
| 330° | 11π / 6 | -2 |
| 345° | 23π / 12 | -√6 – √2 |
| 360° | 2π | undefined |
You might also be interested in our secant and cotangent calculators.
Frequently Asked Questions
Is cosecant the inverse of sine?
Yes, the cosecant function is the inverse, or reciprocal of the sine function. This can be shown as csc(x) = 1/sin(x) and sin(x) = 1/csc(x).
Is the cosecant for a negative angle the same as a positive angle?
No, the cosecant of negative angle identity states that csc(-x) = -csc(x). This means that the cosecant of a negative angle (0x) is equal to the negative of the cosecant of the corresponding positive angle.
Can you find cosecant without a calculator?
To find the cosecant of an angle without a calculator, you need to know the unit circle and the trigonometric ratios. First, identify the reference angle for the given angle. Then, determine the sine of the reference angle, and use the reciprocal of this value to find the cosecant of the original angle.
How do you find cosecant on a calculator?
To find the secant of an angle with a calculator, begin by entering the angle in degrees or radians (depending on what mode your calculator is in). Press the csc button on the calculator.
Note that your calculator may display cosecant as cosec or hyp.
If your calculator has an hyp button, press it followed by the sin button to find the sine of the angle. You can then take the reciprocal to find the cosecant.