Wattage Calculator – Find Power in Watts
Use the wattage calculator below to calculate the power in watts given the voltage, current, or resistance.
Calculation Formulas:
On this page:
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
Aditya holds a PhD in electrical engineering from Stanford University and specializes in signal processing, algorithms, and machine learning.
How to Calculate Wattage
Wattage is a measure of electrical power in watts. You can calculate electrical power with the power formula defined by Watt’s Law, which states that P = I × V, where P is the power in watts, I is the current in amps, and V is the voltage in volts.
Watts Formula
You can express the formula to find the power in watts as:[1]
P(W) = I(A) × V(V)
Thus, the power P in watts is equal to the current I in amps times the voltage V in volts.
You can use this formula to convert amps to watts or volts to watts for DC systems, but there are some additional considerations and formulas for AC circuits.
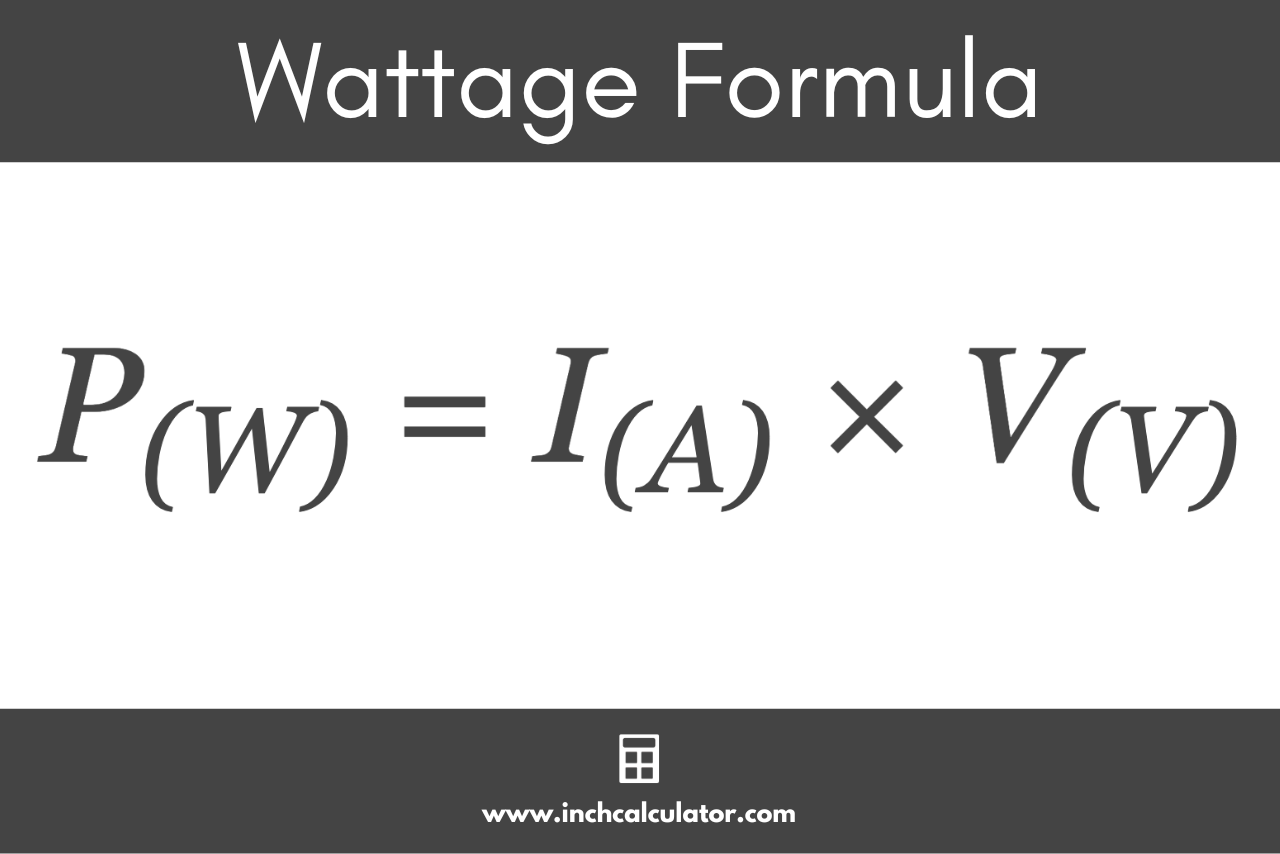
Single-Phase AC Power Formula
Calculating the power draw in watts for single-phase AC circuits using a power factor requires a variation of the watts formula.
P(W) = I(A) × V(V) × PF
The power P in watts is equal to the product of the current I in amps, the voltage V in volts, and the power factor PF.
AC power is composed of real power (also called true power) expressed in watts and reactive power expressed in volt-amps. The magnitude of real and reactive together is the apparent power. The power factor is the ratio of real power to apparent power.[2]
The power factor is determined by the alternating current frequency and the inductive or capacitive elements in the circuit.
You can use our power factor calculator to find the PF value.
Three-Phase AC Power Formula
To calculate wattage for three-phase AC circuits, you will need to account for the phase variation using a different set of formulas.
Line-to-Line Voltage Formula
For three-phase circuits where you know the current, line-to-line RMS voltage, and power factor, the formula to calculate watts is:
P(W) = I(A) × VL-L(V) × PF × √3
The power P in watts is equal to the product of the current I in amps, the line-to-line voltage V in volts, the power factor PF, and the square root of 3.
You can use this equation to calculate the power for one pair of wires in a three-phase system, but you will need to multiply the result by three to find the total power for all three pairs of wires in a three-phase system.
Line-to-Neutral Voltage Formula
For three-phase circuits where you know the current, line-to-neutral RMS voltage, and power factor, the formula to calculate watts is:
P(W) = I(A) × VL-N(V) × PF × 3
The power P in watts is equal to three times the product of the current I in amps, the line-to-neutral voltage V in volts, and the power factor PF.
You can use this formula to find the power delivered by all three wires in a three-phase system, but you will need to divide the result by three to find the power for a single wire in the system.
How to Calculate Watts Using Amps and Ohms
By using Ohm’s Law, you can also find the power in watts given the current in amps and the resistance in ohms using this formula:[1]
P(W) = I(A)2 × R(Ω)
Thus, the power P in watts is equal to the product of the square of current I in amps and the resistance R in ohms.
Frequently Asked Questions
Does higher wattage mean more power?
Yes, the more wattage a component draws, the more energy it will consume. Since watts are a measure of the power drawn through a circuit, higher wattage means higher power draw.
Is more watts good or bad?
Devices or components with higher wattage ratings are not necessarily better or worse, depending on the application and the amount of power available in a circuit.
For instance, a microwave that draws more wattage may cook food faster, but may also increase the likelihood of tripping a circuit breaker if the circuit cannot provide the amount of power required to run it.
Since the amount of wattage drawn is added to your electric bill, drawing more power may also increase the cost of electricity.
Is wattage the same as energy?
Wattage is a measure of electric power, while energy is a measure of power drawn over time. For instance, kilowatts are a measure of power, but kilowatt-hours are a measure of energy.
You can use our kilowatts to kilowatt-hours converter to convert power to energy.
References
- Miller, C., NFPA's Electrical References, National Fire Protection Association, 2004, Jones & Bartlett Learning, 67-75. https://www.google.com/books/edition/NFPA_s_Electrical_References/raUyIi7i-asC
- Fiore, J., AC Electrical Circuit Analysis - A Practical Approach, 2022, 274. http://www.dissidents.com/resources/ACElectricalCircuitAnalysis.pdf