Power Factor Calculator
Find the power factor of a circuit by entering the voltage, current, and real power below. The calculator also solves the apparent power, reactive power, and estimates the size of capacitor needed to correct it.
Results:
| Power Factor: | |
| Apparent Power: | |
| Reactive Power: | |
| Correction Cap: |
On this page:
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
Kevin Weekly holds a PhD in Electrical Engineering and Computer Science (EECS) from the University of California Berkeley and Bachelor's degrees in electrical engineering and computer science from the University of Texas.
How to Calculate Power Factor
Power factor is one driver of the efficiency of energy use in an electrical circuit, and is represented as a number between 0 and 1. There are a few different types of power used in a circuit, and power factor relates to the ratio between them.
True power is the actual power used to do work in a circuit. It is represented as P and often measured in watts (W) or kilowatts (kW).
Reactive power is the power that is moved through the transmission lines of a circuit without doing any real work. It occurs when the current and voltage are not in phase as the result of energy being stored and released by capacitive or inductive loads. It is represented as Q and measured in volt-amperes reactive (VAR) or kilovolt-amperes reactive (kVAR).
Apparent power is the combination of true power and reactive power. It is represented as S and measured in volt-amperes (VA) or kilovolt-amperes (kVA).
The Power Triangle
These three properties can be expressed graphically on what is known as the power triangle.
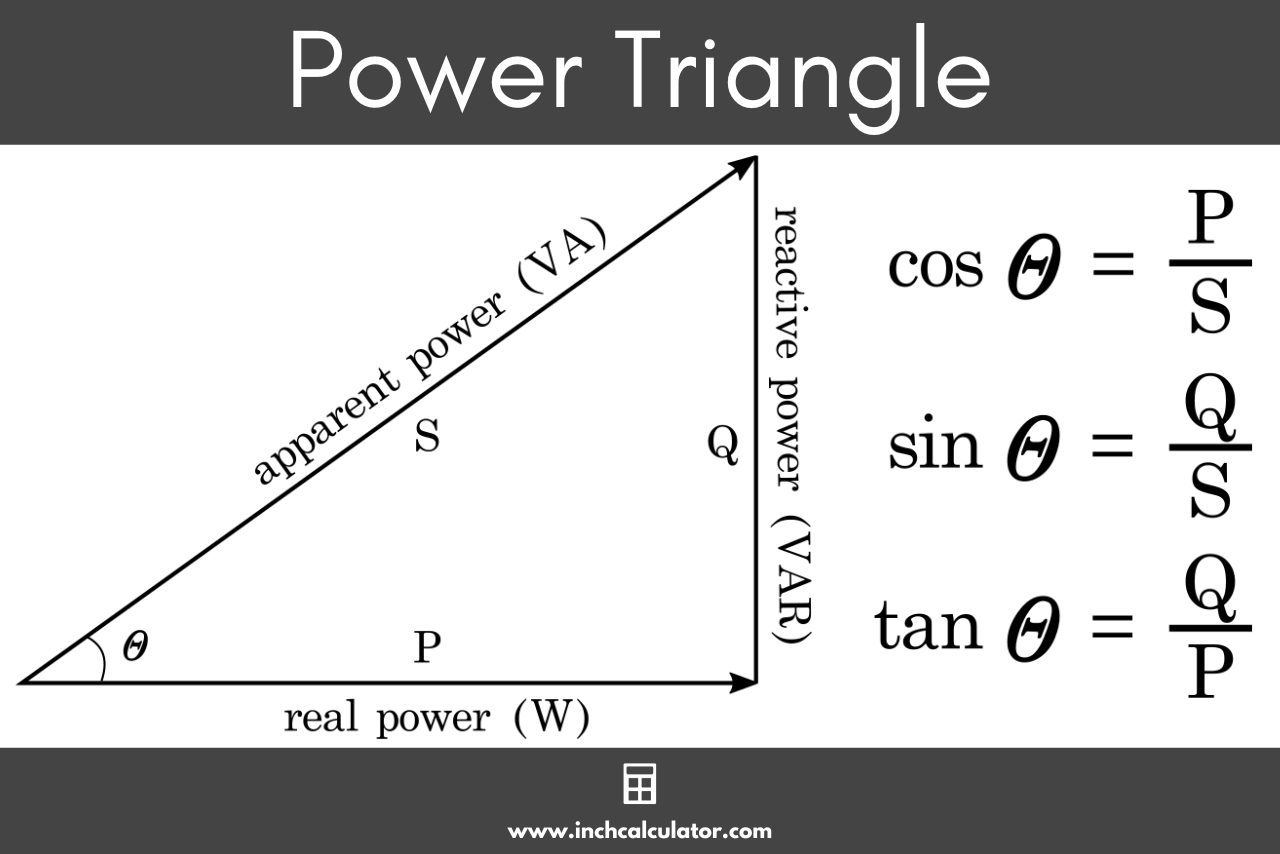
The power triangle is composed of four parts: P, S, Q, and θ. The power triangle is used to calculate power factor.
Power Factor Formulas
The following formulas can be used to solve for power factor:
PF = cos θ = P / S
The power factor PF is equal to the cosine of theta, which is equal to the real power P divided by the apparent power S.
PF = sin θ = Q / S
The power factor PF is equal to the sine of theta, which is equal to the reactive power Q divided by the apparent power S.
PF = tan θ = Q / P
The power factor PF is equal to the tangent of theta, which is equal to the reactive power Q divided by the real power P.
The value of the power factor is dependent on the system AC frequency.
For example, the same device operating in North America at 60Hz will have a different power factor than the same device operating in Europe at 50Hz. In a DC system with constant loads, the system frequency is essentially 0 Hz and power factor is always 1.
Finding Power Factor for a Single Phase Circuit
To calculate power factor for a single phase circuit we need to know the true power and the apparent power. Use the formulas below to solve for PF, apparent power, and reactive power.
Power Factor Formula for Single Phase Circuit
PF = P(W) / (V(V) × I(A))
Apparent Power Formula for Single Phase Circuit
S(VA) = V(V) × I(A)
Reactive Power Formula for Single Phase Circuit
Q(VAR) = √(|S(VA)|2 – P(W)2)
Finding Power Factor for a Three-Phase Circuit
The formula to find power factor on a three-phase circuit is a little different, and requires knowing the line to line voltage. These are the formulas to find power factor on a three-phase AC circuit.
Power Factor Formula for Three-Phase Circuit
PF = P(W) / (√3 × V(V) × I(A))
Apparent Power Formula for Three-Phase Circuit
S(VA) = √3 × V(V) × I(A)
Reactive Power Formula for Three-Phase Circuit
Q(VAR) = √(|S(VA)|2 – P(W)2)
Correcting Power Factor
Because current flow through a circuit is increased as the power factor of an inductive device decreases, this can result in wasted energy through transmission losses. Adding capacitance to the circuit in parallel, near the device can correct for this by compensating for the inductive load.
After correction, the load will then appear to the power source as a resistive load and all of the power being transmitted and generated is consumed to do real work.
To estimate the amount of capacitance needed to correct an inductive load, use the formula below along with the reactive power and system voltage.
capacitance(µF) = 1,000,000 × Q(VAR) / (2 × π × 60(Hz) × V(V)2)
The calculator also estimates the size of the capacitor needed to correct the power factor. It uses this formula and assumes a 60 Hz electrical system.