Average Velocity Calculator

Calculate the average velocity, final velocity, and initial velocity using the average velocity calculator below.

Calculate:

• Average Velocity
• Final Velocity
• Initial Velocity

Initial Velocity (v₀):

ft/s mph cm/s m/s km/h knots

Final Velocity (v₁):

ft/s mph cm/s m/s km/h knots

Final Velocity (v₁):

ft/s mph cm/s m/s km/h knots

Average Velocity (v_avg):

ft/s mph cm/s m/s km/h knots

Initial Velocity (v₀):

ft/s mph cm/s m/s km/h knots

Average Velocity (v_avg):

ft/s mph cm/s m/s km/h knots

×

Have a Question or Feedback?

Name (optional)

Email (optional)

Question or Feedback

Contact Us

Average Velocity:

Average Velocity:

- - - - - - Result Unit ft/s mph cm/s m/s km/h kn

Average Velocity Formula

v_{avg}=\frac{v_{0}+v_{1}}{2}

Final Velocity:

- - - - - - Result Unit ft/s mph cm/s m/s km/h kn

Final Velocity Formula

v_{1}=2v_{avg}-v_{0}

Initial Velocity:

- - - - - - Result Unit ft/s mph cm/s m/s km/h kn

Initial Velocity Formula

v_{0}=2v_{avg}-v_{1}

Learn how we calculated this below

scroll down

Add this calculator to your site

---

On this page:

• Calculator
• How to Calculate Average Velocity
• Average Velocity Formula Using Displacement
• Average Velocity Formula Given Two or More Velocities

---

By

Joe Sexton

Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.

Full bio

Reviewed by

Aditya Dua, PhD

Aditya holds a PhD in electrical engineering from Stanford University and specializes in signal processing, algorithms, and machine learning.

Full bio

Copy Link Share on Facebook Share on X Share on Pinterest Cite

×

Cite As:

Sexton, J. (n.d.). Average Velocity Calculator. Inch Calculator. Retrieved May 6, 2024, from https://www.inchcalculator.com/average-velocity-calculator/

How to Calculate Average Velocity

Velocity is a fundamental concept in physics that describes the rate that an object changes in position with respect to time. Essentially, velocity tells us how fast an object is moving and in which direction.

Velocity is a vector quantity, meaning it has both magnitude (speed) and direction.

The average velocity conveys the overall rate of change in the position of an object over a period of time, while instantaneous velocity conveys the rate of change at a specific moment.

There are several methods to calculate average velocity, depending on what information you have.

Average Velocity Formula Using Displacement

The most common approach to calculating the average velocity is by using displacement. Displacement is the overall change in the position of an object, regardless of the direction or path taken. It is the straight line distance between the initial and final position of the object.

If an object travels a certain displacement in a given time duration, then you can calculate the average velocity using the formula:

The average velocity v_avg is equal to the displacement Δx divided by the time duration Δt. he displacement vector is equal to the vector representing the initial position of the object subtracted from the vector representing the final position of the object.

This is essentially the same method that’s used to calculate speed.

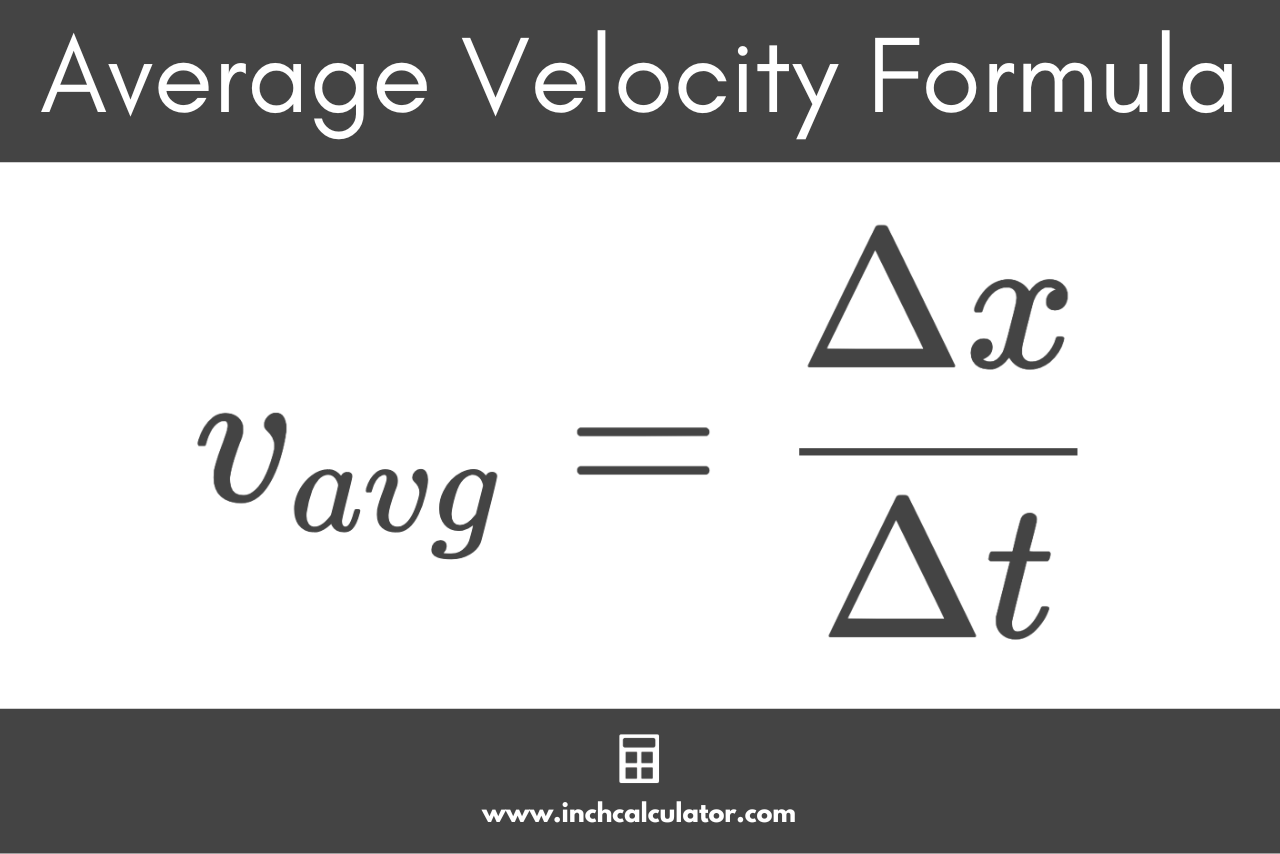
You can also calculate the average velocity given multiple velocities using several formulas.

Average Velocity Formula Given Two or More Velocities

If you know two or more velocities for an object over different periods of time, then you can calculate the average velocity using the average formula:

The average velocity v_avg is equal to the sum of the products of the velocity v_i and time duration t_i for each time interval divided by the total time duration.